Cho Δ ABC cân tại A vẽ các đường cao BH và CK. Chứng minh
a) BK=CH
b) KH//BC
Cho tam giác cân ABC(AB=AC). vẽ các đường cao BH, CK, AI
a, chứng minh BK=CH
b, chứng minh HC.AC=IC.BC
c, chứng minh KH//BC
d, cho biết BC=a, AB=AC=b. tính độ dài đoạn thẳng HK theo a và b
a) Xét ΔBKC vuông tại K và ΔCHB vuông tại H có
BC chung
\(\widehat{KBC}=\widehat{HCB}\)(ΔABC cân tại A)
Do đó: ΔBKC=ΔCHB(cạnh huyền-góc nhọn)
Suy ra: BK=CH(hai cạnh tương ứng)
b) Xét ΔAIC vuông tại I và ΔBHC vuông tại H có
\(\widehat{BCH}\) chung
Do đó: ΔAIC\(\sim\)ΔBHC(g-g)
Suy ra: \(\dfrac{CA}{CB}=\dfrac{CI}{CH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(CA\cdot CH=CB\cdot CI\)(đpcm)
c) Ta có: BK=HC(cmt)
AB=AC(ΔABC cân tại A)
Do đó: \(\dfrac{BK}{AB}=\dfrac{CH}{AC}\)
Xét ΔABC có
K\(\in\)AB(gt)
H\(\in\)AC(gt)
\(\dfrac{BK}{AB}=\dfrac{CH}{AC}\)(cmt)
Do đó: KH//BC(Định lí Ta lét đảo)
Cho tam giác ABC cân tại A. Vẽ các đường cao BH và CK.
a) Chứng minh BK = CH
b) Chứng minh KH // BC
c) Cho BC = 10, AB = 8. Tính HK
a, Xét tam giác BCK và tam giác CBH có
góc B = góc C ( tam giác ABC cân )
BC ( chung )
góc BKC = góc CHB (=90độ )
=> tam giác BCK = tam giác CBH( ch-gn)
=> BK=CH ( 2 cạnh tương ứng )
b, ta có : AK = AB-BK
AH= AC-CH
mà AB=AC ( tam giác ABC cân )
BK=CH( cmt)
=>AK=AH
=> \(\frac{AK}{AB}\) = \(\frac{AH}{AC}\)
Xét tam giác AHK và tam giác ACB có
\(\frac{AK}{AB}=\frac{AH}{AC}\) ( CMT)
=> HK//BC (hq đ/ly talet)
Cho Δ ABC cân tại A. Các đường cao BH,CK
a) Chứng minh Δ ACK = Δ ABH : △BKC = △ CHB
b) Gọi I là giao điểm của BH và CK. Chứng minh AI ⊥BC và AI là tia P/giác của góc BAC
bn tự vẽ hình nhé
a)Xét tam giác ACK và tam giác ABH:
góc K=góc H(=90độ)
AB=AC(gt)
góc A chung
vậy 2 tam giác này bằng nhau (cgv.gnk)
Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h.66).
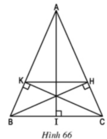
a) Chứng minh BK = CH.
b) Chứng minh KH // BC.
c) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.
Cho tam giác ABC (AB=AC). Vẽ đường cao BH, CK
a, chứng minh BK=CH
b,chứng minh KH // BC
c, cho biết BC=a, AB=AC=b. tính HK ?
a) Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
\(\widehat{KBC}=\widehat{HCB}\)(hai góc ở đáy của ΔBAC cân tại A)
Do đó: ΔKBC=ΔHCB(cạnh huyền-góc nhọn)
Suy ra: BK=CH(hai cạnh tương ứng)
b) Ta có: AK+KB=AB(K nằm giữa A và B)
AH+HC=AC(H nằm giữa A và C)
mà KB=HC(cmt)
và AB=AC(ΔABC cân tại A)
nên AK=AH
Xét ΔABC có
K\(\in\)AB(gt)
H\(\in\)AC(gt)
\(\dfrac{AK}{AB}=\dfrac{AH}{AC}\left(\dfrac{AK}{AH}=\dfrac{AB}{AC}=1\right)\)
Do đó: KH//BC(Định lí Ta lét đảo)
Cho tam giác ABC cân tại A. Vẽ các đường cao BH và CK.
a) Chứng minh BK = CH
b) Chứng minh KH // BC
c) Cho BC = 10, AB = 8. Tính HK
Cho tam giác ABC cân tại A.Vẽ các đường cao BH và CK (H thuộc AC, K thuộc AB)
a/ Chứng minh tam giác BKC đồng dạng với tam giác CHB theo tỉ số đồng dạng bằng 1
b/ Chứng minh KH // BC
c/ Cho biết BC = a, A B = AC = b. Tính độ dài đoạn thẳng KH theo a và b.
a) Xét tam giác BKC và CHB có:
góc B= góc C (tính chất tam giác cân)
góc BKC = góc BHC = 90 độ
=> Tam giác BKC đồng dạng tam giác CHB
=> \(\frac{BK}{CH}=\frac{BC}{BC}=1=k\)
b) Tam giác BHA đồng dạng tam giác CKA (g-g)
=> \(\frac{HA}{AK}=\frac{BA}{AC}=1\)
=> \(\frac{AK}{AB}=\frac{AH}{AC}\)
=> KH//BC (Định lí Ta - lét đảo)
c) Ta có theo hệ quả Ta-let:
\(\frac{AK}{AB}=\frac{KH}{BC}=>\frac{AK}{b}=\frac{KH}{a}=>KH=\frac{a.AK}{b}\)
Ta có: AK2+KC2=b2 (1)
KC2+KB2=a2 => KC2+(b-AK)2=a2 =>KC2-2b.AK+AK2=a2 (2)
Trừ 2 cho 1, ta có: -2b.AK=a2-b2 =>\(AK=\frac{a^2-b^2}{-2b}\)
Từ đó => \(KH=\frac{a\times\frac{a^2-b^2}{-2b}}{b}\)
Cho tam giác cân ABC(AB=AC). vẽ các đường cao BH, CK, AI
a, chứng minh BK=CH
b, chứng minh HC.AC=IC.BC
c, chứng minh KH//BC
d, cho biết BC=a, AB=AC=b. tính độ dài đoạn thẳng HK theo a và b
cho tam giác cân ABC (AB=AC) . Vẽ các đường cao BH,CK,AI
a) chứng minh BK=CH
b chứng minh HC.AC=IC.BC
c C/M KH//BC
d cho bt BC =a, AB=AC=b . tính HK theo a và b