Cho tam giác ABC vuông tại A có AH là đường cao.Biết AB=6cm,AC=8cm.Tính độ dài đường cao AH
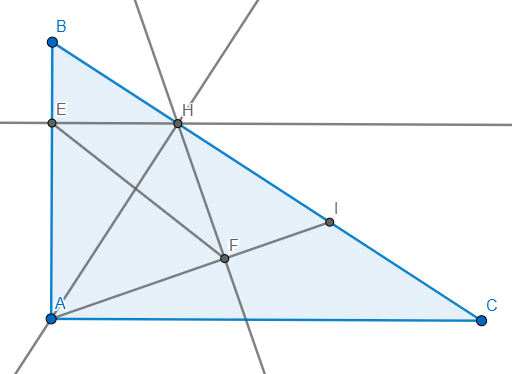
Cho tam giác ABC vuông tại A,đường cao AH(H thuộc BC) 1/Giả sử AB=6cm,AC=8cm.Tính độ dài BC,AH 2/Kẻ HE vuông góc với AB tại E.Gọi I là trung điểm của HC.Kẻ HF vuông góc với AI tại F. Chứng minh tam giác AEF đồng dạng với tam giác AIB.
a) tam giác ABC vuông tại A nên áp dụng Py-ta-go:
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4.8\left(cm\right)\)
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHI vuông tại H có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AI=AH^2\Rightarrow AF.AI=AE.AB\Rightarrow\dfrac{AF}{AB}=\dfrac{AE}{AI}\)
Xét \(\Delta AEF\) và \(\Delta AIB:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AE}{AI}=\dfrac{AF}{AB}\\\angle BAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta AIB\left(c-g-c\right)\)
1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
cách tính bài cho tam giác ABC vuông Tại A có AH là đường cao.biết AB=15cm,BC=25cm.tính độ dài các cạnh AC BH AH
Tam giác ABC vuông tại A. Áp dụng Pitago
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2=25^2-15^2=400\left(cm\right)\)
=> AC = 20 (cm)
Tam giác ABC vuông tại A có AH là đường cao
\(\Rightarrow AB^2=BH.BC\)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
Tam giác ABH vuông tại H. Áp dụng Pitago
\(\Rightarrow AB^2=BH^2+AH^2\)
\(\Rightarrow AH^2=AB^2-BH^2=15^2-9^2=144\left(cm\right)\)
=> AH = 12 (cm)
Tam giác ABC vuông tại A. Áp dụng Pitago
BC2=AB2+AC2BC2=AB2+AC2
⇒AC2=BC2−AB2=252−152=400(cm)⇒AC2=BC2−AB2=252−152=400(cm)
=> AC = 20 (cm)
Tam giác ABC vuông tại A có AH là đường cao
⇒AB2=BH.BC⇒AB2=BH.BC
Cho ABC vuông tại A,AH là đường cao(AB<AC)
a)chứng minh tam giá ABC đồng dạng với tam giác HAC từ đó suy ra CA2= HC nhân BC
b)vẽ tia phân giác của góc ABC cắt AH tại I,cắt AC tại E chứng minh IH/IA = BI/BE
C)giả sử AB=6cm,AC=8cm.Tính độ dài AE và CE
1.Cho tam giác ABC vuông tại A , đường phân giác BE , biết EC=3cm ,BC=6cm . Tính độ dài các đoạn thẳng AB, AC .
2.Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=3:7 , AH=42cm.Tính độ dài BH , CH
3.Cho tam giác ABC vuông tại A , đường cao AH . Biết BH:CH=9:16 , AH-48cm.Tính độ dài các cạnh góc vuông của tam giác ABC
4.Cho tam giác ABC vuông tại A ,phân giác AD , đường cao AH. Biết AB=21cm,AC=28cm .Tính HD
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, BC = 10cm
a) Tính độ dài AC.
b) Tính diện tích tam giác ABC.
c) Tính độ dài đường cao AH.
a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Kẻ đường cao AH. Tính độ dài cạnh AH.
Theo \(pi-ta-go\) ta có : \(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\) \((cm)\)
Áp dụng hệ thức lượng vào tam giác \(ABC\) vuông và đường cao \(AH\) ta có :
\(AH.BC=AB.AC\)\(\Rightarrow\) \(AH=\dfrac{6.8}{10}=4,8(cm)\)
- Áp dụng định lý Pytago
=> BC=10 (cm)
- Gọi HB=a (cm) ; HC=b (cm)
=> a+b=BC=10 (1)
- Xét \(\Delta\)HBA và \(\Delta\)ABC có:
BHA=BAC=90\(^o\)
BAC chung
=> \(\Delta\)HBA ~ \(\Delta\)ABC (g.g)
=> \(\dfrac{BH}{AB}\)=\(\dfrac{AB}{BC}\) (cạnh t/ư)
=> BH.BC=AB2 (tỉ lệ thức)
thay số: a.10= 36 (2)
Từ (1)(2) => a=3,6 (cm); b=6,4 (cm)
- Áp dụng Pytago cho \(\Delta\)HBA
=> AH2=AB2- HB2 =36-12,96=23,04 (cm)
=> AH=4,8 (cm)
P/s: Vì không nhớ lớp 8 học hệ thức lượng chưa nên đành phải lôi thôi thế này :<<<<
Cho tam giác abc vuông tại A,đường cao AH, phân giác BD cắt AH tại I.
a) cmr:tấm giác AID cân
b) cho biết AB=6cm, AC=8cm.tính BC,AH,BD
Cho tam giác ABC vuông tại A có AH là đường cao.Biết HB=4cm,BC=9cm.Tính độ dài của canh AB
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow AB^2=4\cdot9=36\)
hay AB=6(cm)
Vậy: AB=6cm
Bài 1 : Tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, AC = 8cm.Tính BC, AH, BH, Tính góc C làm tròn đếnđộ
BC=10cm
AH=4,8cm
BH=3,6cm
\(\widehat{C}=37^0\)