\(a,9x^2+y^2+2z^2-18x+4z-6y+20=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)

\(b,5x^2+5y^2+8xy+2y-2x+2=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

\(c,5x^2+2y^2+4xy-2x+4y+5=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

\(d,x^2+4y^2+z^2=2x+12y-4z-14\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)

\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)

Pt vô nghiệm do ko có 2 bình phương số nguyên có tổng là 11

e: Ta có: \(x^2-6x+y^2+4y+2=0\)

\(\Leftrightarrow x^2-6x+9+y^2+4y+4-11=0\)

\(\Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)

Dấu '=' xảy ra khi x=3 và y=-2

\(a,\Leftrightarrow\left(9x^2-18x+9\right)+\left(y^2-6y+9\right)+\left(2z^2+4z+2\right)=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)

\(b,\Leftrightarrow\left(4x^2+8xy+4y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

\(c,\Leftrightarrow\left(4x^2+4xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2+4y+4\right)=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

a,9x^2+y^2+2z^2−18x+4z−6y+20=0

⇔9(x−1)^2+(y−3)^2+2(z+1)^2=0

⇔x=1;y=3;z=−1

b,5x^2+5y^2+8xy+2y−2x+2=0

⇔4(x+y)2+(x−1)2+(y+1)2=0

⇔x=−y;x=1y=−1⇔x=1y=−1

c,5x^2+2y^2+4xy−2x+4y+5=0

⇔(2x+y)^2+(x−1)^2+(y+2)^2=0

⇔2x=−y;x=1;y=−2

⇔x=1;y=−2

⇔(x−1)^2+(2y−3)^2+(z+2)^2=0

\(d,\Leftrightarrow\left(x^2-2x+1\right)+\left(4y^2-12y+9\right)+\left(z^2+4z+4\right)=0\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)

\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)

\(\Rightarrow\)PT vô nghiệm vì 11 không phải là tổng 2 số chính phương

a: ta có: \(x^2+3x-\left(2x+6\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)

b: Ta có: \(5x+20-x^2-4x=0\)

\(\Leftrightarrow\left(x+4\right)\left(5-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=5\end{matrix}\right.\)

\(b,\Rightarrow\left(x+2\right)\left(x+2-x+3\right)=0\\ \Rightarrow5\left(x+2\right)=0\\ \Rightarrow x=-2\\ c,\Rightarrow2x\left(x^2-2x+1\right)=0\\ \Rightarrow2x\left(x-1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\\ d,\Rightarrow\left(x-1-2x-1\right)\left(x-1+2x+1\right)=0\\ \Rightarrow3x\left(-x-2\right)=0\\ \Rightarrow-3x\left(x+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}-3x=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)

a)thiếu dấu

b)(x+2)² -(x+2)(x-3)=0

(x+2)(x+2-x+3)=0

(x+2)5=0

x+2=0

x=-2

c)2x³-4x²+2x=0

2x(x²-2x+1)=0

2x(x-1)²

suy ra 2 trường hợp

x=0

x-1=0=>x=1

d)(x-1)²-(2x+1)²=0

(x-1-2x-1)(x-1+2x+1)=0

(x-2)3x=0

x=0

x=2

\(a,\Leftrightarrow x\left(2x-7\right)+2\left(2x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(2x-7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{7}{2}\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ c,\Leftrightarrow\left(2x-1\right)\left(2x+1\right)-2\left(2x-1\right)^2=0\\ \Leftrightarrow\left(2x-1\right)\left(2x+1-4x+2\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(-2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

c: =>(x-1)(x+1)=0

hay \(x\in\left\{1;-1\right\}\)

plss

a,

\(=\dfrac{3}{4x}.\left(x-3\right)\left(x+3\right)\)=0

\(\left\{{}\begin{matrix}\dfrac{3}{4x}=0\\x-3=0\\x+3=0\end{matrix}\right.\)

=>\(x=\left\{3,-3\right\}\)

b,

\(x^3-16x=0\\x\left(x^2-16\right)\\ x\left(x-4\right)\left(x+4\right)\)

\(\left\{{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\)

=>\(x=\left\{-4,0,4\right\}\)

d,

\(3x^3-27x=0\\ 3x\left(x^2-9\right)=0\\ 3x\left(x-3\right)\left(x+3\right)=0\)

\(\left\{{}\begin{matrix}3x=0\\x-3=0\\x+3=0\end{matrix}\right.\)

=>\(x=\left\{-3,0,3\right\}\)

e,

\(x^2+\left(x+1\right)+2x\left(x+1\right)=0\\ x\left(x+1\right)\left(x+2\right)=0\)

\(\left\{{}\begin{matrix}x=0\\x+1=0\\x+2=0\end{matrix}\right.\)

=>\(x=\left\{-2,-1,0\right\}\)

f,

\(x\left(2x-3\right)-2\left(3-2x\right)=0\\ \left(2x-3\right)\left(x+2\right)=0\)

\(\left\{{}\begin{matrix}2x-3=0\\x+2=0\end{matrix}\right.\left\{{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\)

a) Ta có: \(x^3+x^2+x+1=0\)

\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)

mà \(x^2+1>0\forall x\)

nên x+1=0

hay x=-1

Vậy: S={-1}

b) Ta có: \(x^3-6x^2+11x-6=0\) 

\(\Leftrightarrow x^3-x^2-5x^2+5x+6x-6=0\)

\(\Leftrightarrow x^2\left(x-1\right)-5x\left(x-1\right)+6\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\end{matrix}\right.\)

Vậy: S={1;2;3}

c) Ta có: \(x^3-x^2-21x+45=0\)

\(\Leftrightarrow x^3-3x^2+2x^2-6x-15x+45=0\)

\(\Leftrightarrow x^2\left(x-3\right)+2x\left(x-3\right)-15\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x^2+2x-15\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x^2+5x-3x-15\right)=0\)

\(\Leftrightarrow\left(x-3\right)^2\cdot\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)

Vậy: S={3;-5}

d) Ta có: \(x^4+2x^3-4x^2-5x-6=0\)

\(\Leftrightarrow x^4-2x^3+4x^3-8x^2+4x^2-8x+3x-6=0\)

\(\Leftrightarrow x^3\left(x-2\right)+4x^2\cdot\left(x-2\right)+4x\left(x-2\right)+3\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^3+4x^2+4x+3\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^3+3x^2+x^2+4x+3\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+3\right)+\left(x+1\right)\left(x+3\right)\right]=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+3\right)\left(x^2+x+1\right)=0\)

mà \(x^2+x+1>0\forall x\)

nên (x-2)(x+3)=0

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)

Vậy: S={2;-3}

a) Phương trình bậc hai:  7 x 2   –   2 x   +   3   =   0

Có: a = 7; b = -2; c = 3;  Δ   =   b 2   –   4 a c   =   ( - 2 ) 2   –   4 . 7 . 3   =   - 80   <   0

Vậy phương trình vô nghiệm.

b) Phương trình bậc hai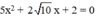 

Có: a = 5; b = 2√10; c = 2;  Δ   =   b 2   –   4 a c   =   ( 2 √ 10 ) 2   –   4 . 2 . 5   =   0

Vậy phương trình có nghiệm kép.

c) Phương trình bậc hai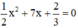 

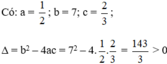
Vậy phương trình có hai nghiệm phân biệt.

d) Phương trình bậc hai  1 , 7 x 2   –   1 , 2 x   –   2 , 1   =   0

Có: a = 1,7; b = -1,2; c = -2,1; 

Δ   =   b 2   –   4 a c   =   ( - 1 , 2 ) 2   –   4 . 1 , 7 . ( - 2 , 1 )   =   15 , 72   >   0

Vậy phương trình có hai nghiệm phân biệt.

Kiến thức áp dụng

Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.

+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt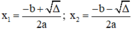 

+ Nếu Δ = 0, phương trình có nghiệm kép  ;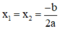

+ Nếu Δ < 0, phương trình vô nghiệm.

a) (x-4)(x+4)-x(x+2)=0

     x²-16-x²-2x = 0

     -16 - 2x = 0

             2x = -16 

               x = -16/2

               x = -8

b) 3x(x-2)-x+2=0

     (3x-1)(x-2)=0

=> x ∈ {1/3 ; 2 }

c) 6x - 12x² = 0

    6x(1-2x) = 0

=> x ∈ {0; 1/2 }

d) mình thấy có vẻ hơi sai đề nên mình ko giải được, bạn thông cảm nha

d/ 4x (3 - ¹/₄ x) + (x -2) ( x+ 2)

câu d bị  sai đề