Trong hệ trục tọa độ cho đường tròn tâm I(1 ; -1) bán kính 4. Hãy xác định vị trí tương đối của điểm M(3 ; 3) đối với đường tròn?

Những câu hỏi liên quan
Trong hệ trục tọa độ Oxy, cho điểm I(1;1) và đường thẳng (d):3x+4x-20 Đường tròn tâm I và tiếp xúc với đường thẳng (d) có phương trình A.
x
-
1
2
+
y
-
1
2...
Đọc tiếp
Trong hệ trục tọa độ Oxy, cho điểm I(1;1) và đường thẳng (d):3x+4x-2=0 Đường tròn tâm I và tiếp xúc với đường thẳng (d) có phương trình
A. x - 1 2 + y - 1 2 = 5 .
B. x - 1 2 + y - 1 2 = 25 .
C. x - 1 2 + y - 1 2 = 1 .
D. x - 1 2 + y - 1 2 = 1 5 .
Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho tam giác ABC vuông tại A với B(-3;0) và C(7;0) , bán kính đường tròn nội tiếp tam giác là r= 2√10 -5. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết I có tung độ dương.
Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho tam giác ABC vuông tại A với B(-3;0) và C(7;0) , bán kính đường tròn nội tiếp tam giác là r=2√10-5
. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết I có tung độ dương.
Trong mặt phẳng hệ trục tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I; E (1/2;1/2) là trung điểm AB. H (4/5;-22/5) là tọa độ hình chiếu vuông góc của A lên CI. Ptdt BC : x+y-4=0. Tìm tọa độ A,B,C
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn (C):
x
2
+
y
2
−
2
x
−
4
y
+
2
0
. Phép đối xứng qua tâm O biến đường tròn (C) thành đường tròn nào trong các đường tròn có phương trình sau: A.
(
x
−
1
)
2
+
(...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn (C): x 2 + y 2 − 2 x − 4 y + 2 = 0 . Phép đối xứng qua tâm O biến đường tròn (C) thành đường tròn nào trong các đường tròn có phương trình sau:
A. ( x − 1 ) 2 + ( y − 2 ) 2 = 3
B. ( x + 2 ) 2 + ( y + 1 ) 2 = 3
C. ( x + 1 ) 2 + ( y + 2 ) 2 = 3
D. ( x + 1 ) 2 + ( y − 2 ) 2 = 3
Đáp án C
(C) có tâm I(1;2) bán kính R = 3
Đ O : I → I’(–1;–2)
Phương trình đường tròn (C’): x + 1 2 + y + 2 2 = 3
Đúng 0
Bình luận (0)
Trên hệ trục tọa độ Oxy, cho đường tròn (C) có tâm I(-3;2) và một tiếp tuyến của nó có phương trình là: 3x+4y-90. Viết phương trình của đường tròn (C) A.
x
+
3
2
+
y
-
2
2
2
B. ...
Đọc tiếp
Trên hệ trục tọa độ Oxy, cho đường tròn (C) có tâm I(-3;2) và một tiếp tuyến của nó có phương trình là: 3x+4y-9=0. Viết phương trình của đường tròn (C)
A. x + 3 2 + y - 2 2 = 2
B. x - 3 2 + y + 2 2 = 2
C. x - 3 2 + y + 2 2 = 4
D. x + 3 2 + y - 2 2 = 4
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2;2;1),
B
-
8
3
;
4
3
;
8
3
. Biết I(a;b;c) là tâm đường tròn nội tiếp của tam giác OAB. Tính tổng S a + b + c A. S 1 B. S -1 C. S 0 D...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2;2;1), B - 8 3 ; 4 3 ; 8 3 . Biết I(a;b;c) là tâm đường tròn nội tiếp của tam giác OAB. Tính tổng S =a + b + c
A. S = 1
B. S = -1
C. S = 0
D. S = 2
Đáp án D
Cách 1 (Véc tơ đơn vị). Ta có
![]()
=> Tam giác OAB vuông tại O
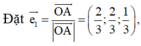
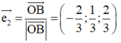

Gọi H, E là các tiếp điểm của đường tròn nội tiếp với các cạnh OA, OB.
Ta có
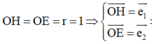
![]()
Cách 2. Kẻ phân giác OE suy ra
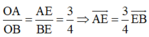
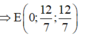
Gọi I là tâm đường tròn nội tiếp tam giác OAB
![]()
Tam giác OAB vuông tại O, có bán kính đường tròn nội tiếp r =1 ⇒ I O = 2
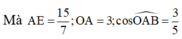
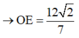
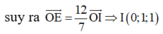
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (S) có tâm I nằm trên đường thẳng
y
-
x
, bán kính bằng
R
3
và tiếp xúc với các trục tọa độ. Lập phương trình của (S), biết hoành độ tâm I là số dương. A.
x
-
3
2
+
y
-
3...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (S) có tâm I nằm trên đường thẳng y = - x , bán kính bằng R = 3 và tiếp xúc với các trục tọa độ. Lập phương trình của (S), biết hoành độ tâm I là số dương.
A. x - 3 2 + y - 3 2 = 9
B. x - 3 2 + y + 3 2 = 9
C. x - 3 2 - y - 3 2 = 9
D. x + 3 2 + y + 3 2 = 9
Gọi I a ; - a a > 0 thuộc đường thẳng y = - x
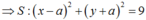
(S) tiếp xúc với các trục tọa độ
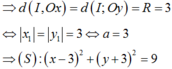
Chọn B.
Đúng 0
Bình luận (0)
Trong hệ trục Oxy cho ba điểm A(1;1) ; B(4;1) ; C(1;5) . Xác định tọa độ tâm đường tròn nội tiếp ∆ABC








