Giúp nhanh cảm ơn :>

Những câu hỏi liên quan
Giúp mik nhe nhanh nhanh nhe cảm ơn nhìu 
a.Zn + 2HCl -> ZnCl2 + H2
b.Định luật bảo toàn khối lương: mZn + mHCl = mZnCl2 + mH2
c.mZn = mZnCl2 + mH2 - mHCl = 13.6 + 0.2 - 7.3 = 6.5g
Đúng 0
Bình luận (0)
tính nhanh
202,1 : 0,125 + 202,1 : 0,2 - 202,1 : 1/3
nhanh nhanh giúp mình với , mình đang thi , 40 phút thôi
please , ai làm được nhanh mình tick cho
nhớ ơn cả đời
cầu xin đó , nhanh nhanh giùm mình
mình cảm ơn , ngàn lần cảm ơn , vạn lần cảm ơn !!!!!!!!!!!!!!!!!
202,1 : 0,125 + 202,1 : 0,2 - 202,1 : 1/3
= 202,1 x 8 + 202,1 x 5 - 202,1 x 3
= 202,1 x (8 + 5 - 3)
= 202,1 x 10
= 2021
Chắc vậy đó bạn!
202,1 : 0,125 + 202,1 : 2 - 202,1 : 1/3
= 202,1 x 8 + 202,1 x 5 - 202,1 x 3
= 202,1 x ( 8 + 5 - 3 )
= 202,1 x 10
= 2021
~ Hok T ~
cầu xin các bạn đấy , giúp mình đi
Xem thêm câu trả lời
Nhanh giúp em ạ cảm ơn
mouth , south , house, cloud , town , tower, about, crowded, count : au
còn lại là của cái kia. theo mình là vậy
Đúng 1
Bình luận (1)

Giúp mình nhanh nha cảm ơn
a: \(\widehat{A}=\widehat{D}\)
Đúng 1
Bình luận (1)
 giúp với nhanh nha cảm ơn
giúp với nhanh nha cảm ơn
\
| tổng | 91 | 170 | 216 |
| tỉ số | 1:6 | 2:3 | 3:5 |
| sl | |||
| sb |
Đúng 0
Bình luận (0)
Giúp nhanh ạ, e cảm ơn 
1) DC cắt AB tại H.
- Ta có: \(\widehat{DAB}+\widehat{BAC}=\widehat{DAC}\) ; \(\widehat{CAE}+\widehat{BAC}=\widehat{BAE}\).
Mà \(\widehat{DAB}=\widehat{CAE}=60^0\) (△ABD đều, △ACE đều).
=>\(\widehat{DAC}=\widehat{BAE}\)
- Xét △DAC và △BAE có:
\(\left[{}\begin{matrix}AD=AB\left(\Delta ABDđều\right)\\\widehat{DAC}=\widehat{BAE}\left(cmt\right)\\AC=AE\left(\Delta ACEđều\right)\end{matrix}\right.\)
=>△DAC = △BAE (c-g-c).
=>\(\widehat{ADC}=\widehat{ABE}\) (2 góc tương ứng).
- Ta có: \(\widehat{ADH}+\widehat{HAD}+\widehat{AHD}=180^0\) (tổng 3 góc trong △DAH).
\(\widehat{MBH}+\widehat{BMH}+\widehat{BHM}=180^0\) (tổng 3 góc trong △BMH).
Mà \(\widehat{ADH}=\widehat{MBH}\) (cmt) ; \(\widehat{BHM}=\widehat{AHD}\) (đối đỉnh).
=>\(\widehat{DAH}=\widehat{HMB}\) mà \(\widehat{DAH}=60^0\) (△ABD đều).
=>\(\widehat{HMB}=60^0\).
Mà \(\widehat{HMB}+\widehat{BMC}=180^0\) (kề bù).
=>\(60^0+\widehat{BMC}=180^0\)
=>\(\widehat{BMC}=120^0\).
2) Ta có: MF=MB (gt) nên △MBF cân tại M.
Mà \(\widehat{FMB}=60^0\) (cmt) nên △MBF đều.
=> \(\widehat{FBM}=60^0\) mà \(\widehat{ABD}=60^0\) (△ABD đều) nên \(\widehat{FBM}=\widehat{ABD}=60^0\)
Mà \(\widehat{FBH}+\widehat{ABM}=\widehat{FBM}\); \(\widehat{FBH}+\widehat{DBF}=\widehat{ABD}\).
=>\(\widehat{DBF}=\widehat{ABM}\)
- Xét △BFD và △BMA có:
\(\left[{}\begin{matrix}BD=BA\left(\Delta ABDđều\right)\\\widehat{DBF}=\widehat{ABM}\left(cmt\right)\\BF=BM\left(\Delta BMFđều\right)\end{matrix}\right.\)
=>△BFD = △BMA (c-g-c).
3) - Ta có: \(\widehat{DFB}+\widehat{BFM}=180^0\) (kề bù).
Mà \(\widehat{BFM}=60^0\) (△BFM đều) nên \(\widehat{DFB}+60^0=180^0\)
=>\(\widehat{DFB}=120^0\) mà \(\widehat{DFB}=\widehat{AMB}\) (△BFD = △BMA)
Nên \(\widehat{AMB}=120^0\)
Đúng 1
Bình luận (0)
giúp mình nhanh nha,cảm ơn

1. C
2. D
3. C
4. C
5. C
6. D
7. A
8. A
9. D
10. D
11. C
12. C
13. C
17. C
18. B
20. C
Đúng 2
Bình luận (0)
1 C
2 D
3 C
4 A
5 C
6 D
7 A
8 A
9 D
10 D
11 C
12 C
13 C
17 C
18 B
20 C
Đúng 0
Bình luận (0)
Giải giúp mình Bài 1 với, nhanh nhanh nha, cảm ơn nhiều
Bài 1:
Xét ΔDEF có
M là trung điểm của DE
P là trung điểm của DF
Do đó: MP là đường trung bình
=>MP//EF
=>ΔDMP\(\sim\)ΔDEF
Xét ΔDEF có
M là trung điểm của ED
N là trung điểm của FE
Do đó: MN là đường trung bình
=>ΔEMN\(\sim\)ΔEDF
Xét ΔDEF có
P là trung điểm của DF
N là trung điểm của EF
Do đó: PN là đường trung bình
=>PN//DE
hay ΔFPN\(\sim\)ΔFDE
Đúng 0
Bình luận (0)
Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...
Đọc tiếp

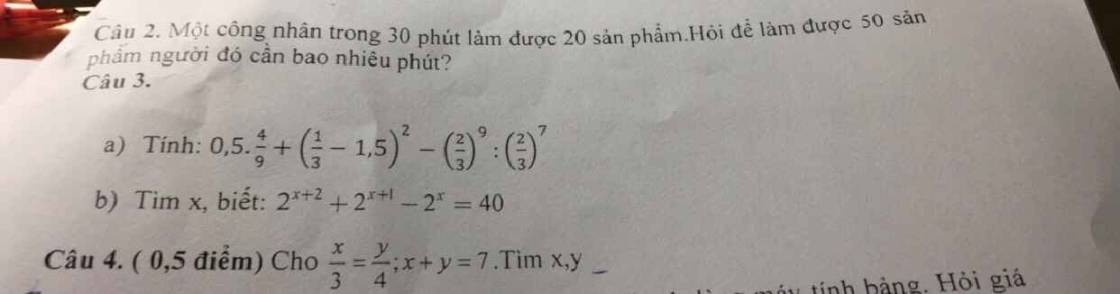 Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...
Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...![]()
























