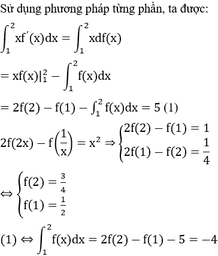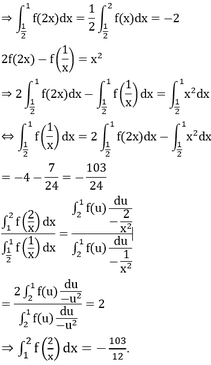cho mình hỏi (f(2x))' có = 2f'(2x) k z

Những câu hỏi liên quan
Giúp mình với :
Cho y=f(x)= 2f(x)-f(1/x)=2x^2-1. Tính f(7)
Cho x=7 ta có:\(y=f\left(7\right)=2f\left(7\right)-f\left(\frac{1}{7}\right)=2.7^2-1=97\)
Vậy \(f\left(7\right)=97\)
Hình như đề sai thì phải bạn ak
Đúng 0
Bình luận (0)
cho mk hỏi phân thức \(\frac{x^2-2017}{1+x^{2018}}\) được xác định khi
Đúng 0
Bình luận (0)
Cho đa thức f(x) thỏa mãn f(x)+2f(3/2x^2-1/2x-1)=x^3-x+3 với mọi x.Chứng minh rằng f(1)+f(-1)=2f(0)
Cho f(x)=5x^3 -7x^2 +2x+5
h(x)=2x^3 +4x+1
g(x)= 7x^3 -7x^2 +2x +5
a)tính f(1) ,g(1/2),h(0)
b)tính k(x)= f(x) -g(x) +h(x) m(x)=3h(x) -2f(x)
c) tìm bậc của k(x),tìm nghiệm của k(x)
a) \(f\left(x\right)=5x^3-7x^2+2x+5\)
\(\Rightarrow f\left(1\right)=5.1^3-7.1^2+2.1+5\)
\(\Rightarrow f\left(1\right)=5.1-7.1+2+5\)
\(\Rightarrow f\left(1\right)=5-7+7\)
\(\Rightarrow f\left(1\right)=5\)
Vậy f(1) = 5.
\(g\left(x\right)=7x^3-7x^2+2x+5\)
\(\Rightarrow g\left(\frac{1}{2}\right)=7.\left(\frac{1}{2}\right)^3-7.\left(\frac{1}{2}\right)^2+2.\frac{1}{2}+5\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=7.\frac{1}{8}-7.\frac{1}{4}+1+5\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=\frac{7}{8}-\frac{14}{8}+6\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=\frac{-7}{8}+\frac{48}{8}\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=\frac{41}{8}\)
Vậy \(g\left(\frac{1}{2}\right)=\frac{41}{8}\)
Đúng 0
Bình luận (0)
\(h\left(x\right)=2x^3+4x+1\)
\(\Rightarrow h\left(0\right)=2.0^3+4.0+1\)
\(\Rightarrow h\left(0\right)=0+0+1\)
\(\Rightarrow h\left(0\right)=1\)
Vậy \(h\left(0\right)=1\)
Đúng 0
Bình luận (0)
b)\(f\left(x\right)-g\left(x\right)+h\left(x\right)\)
\(=5x^3-7x^2+2x+5-2x^3-4x-1+7x^3-7x^2+2x+5\)
Rút gọn rồi tìm k(x)
Tìm M(x) tương tự
c) Bậc của k(x) là đơn thức có bậc cao nhất là 3
Nghiệm của k(x) là khi k(x) = 0 . Như câu a)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
F(x)=8x^4-2x^2-1/2x-1
G(x)=-2x^6-6x^3+x^2+7
a) Tính h(x)= 2f(x)+g(x)
K(x)= f(x)- g(x)
b) Tính giá trị của k(x) tại 2x-1=-3
f(x)+2f(3/2x^2-1/2x-1)=x^3-x+3 với mọi x,chứng minh f(1)+f(-1)=2f(0)
Tao ko phải tiên tri nhưng tao biết có đứa đang check bài này của tao🙃
Xem chi tiết
xàm xí quá di thưi
:))) rảnh quá dzậy bn ?
Cho hàm số f(x) có đạo hàm liên tục trên R{0} và thỏa mãn 2f(2x)-f(1/x)
x
2
,
∫
1
2
xf
(
x
)
dx
5
. Giá trị dx
∫
1
2
f
(
2...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên R\{0} và thỏa mãn 2f(2x)-f(1/x)= x 2 , ∫ 1 2 xf ' ( x ) dx = 5 . Giá trị dx ∫ 1 2 f ( 2 x ) bằng
A. -103/48.
B. 103/24.
C. 103/48.
D. -103/12
Cho hàm số y f(x) có đạo hàm liên tục trên R, thỏa mãn 2f(2x) + f(1 – 2x) 12x2. Phương trình tiếp tuyến của đồ thị hàm số y f(x) tại điểm có hoành độ bằng 1 là A. y 4x - 6 B. y 2x - 6 C. y 4x - 2 D. y 2x + 2
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R, thỏa mãn 2f(2x) + f(1 – 2x) = 12x2. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ bằng 1 là
A. y = 4x - 6
B. y = 2x - 6
C. y = 4x - 2
D. y = 2x + 2
F(x)=8x^4-2x^2-1/2x-1
G(x)=-2x^6-6x^3+x^2+7
a) Tính h(x)= 2f(x)+g(x)
K(x)= f(x)- g(x)
b) Tính giá trị của k(x) tại 2x-1=-3
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
-
2
x
,
∀
x
∈
R
. Hàm số y-2f(x) đồng biến trên khoảng A.
(
0
;
2
)
B.
(
-
2
;
0
)
C.
(
2
;
+
∞
)
D.
(...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 - 2 x , ∀ x ∈ R . Hàm số y=-2f(x) đồng biến trên khoảng
A. ( 0 ; 2 )
B. ( - 2 ; 0 )
C. ( 2 ; + ∞ )
D. ( - ∞ ; - 2 )