Tìm y :Biết Yx2+y/2=10
Những câu hỏi liên quan
Tìm y biết :Yx4 +yx6 +yx8 +yx2 =200
y x (4+6+8+2)= 200
y x 20 =200
y = 200 : 20
y= 10
Đúng 1
Bình luận (0)
Cho x,y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-...
Đọc tiếp
Cho x,y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 9 + y y - 9 + x y . Tìm giá trị lớn nhất của biểu thức P = 3 x + 2 y - 9 x + y - 10 khi x,y thay đổi.
A. 2
B. 3
C. 1
D. 0
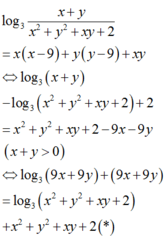
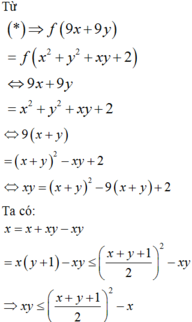
Từ đó
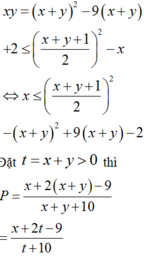
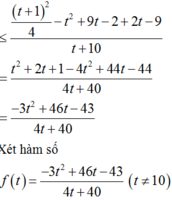
Sử dụng MTCT ta tìm được max P = 2 .
Chọn A.
Đúng 0
Bình luận (0)
yx2+ y/2=10
tìm x,y
x2 + (y + 1)2 = 1
Tìm tất cả các cặp x y hay có cho điều kiện của x y ko bạn
Đúng 0
Bình luận (0)
giá trị của y thỏa mãn:
yx2+y/2 =10
Tìm Y biết15+y+4+y+9+y+yx2=58
Giải giúp mình với mình đang cần gấp
Xem chi tiết
Tìm cặp số nguyên x ,y
x2 -2xy+ 5y2 = y-1
\(\Leftrightarrow x^2-2xy+5y^2-y+1=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(4y^2-y+\dfrac{1}{16}\right)+\dfrac{15}{16}=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(2y-\dfrac{1}{4}\right)^2+\dfrac{15}{16}=0\) (vô nghiệm)
Ko tồn tại x; y thỏa mãn pt
Đúng 3
Bình luận (0)
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x(x - 3) + y(y - 3) + xy. Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6
A. Pmax = 0
B. Pmax = 2
C. Pmax = 1
D. Pmax = 3
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
<=> 
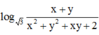
(2)
Đặt 
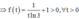
=> f(t) đồng biến trên (0;+∞)
<=> 
<=> 
Khi đó,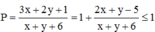 
vì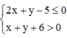 
Vậy Pmax = 1 khi và chỉ khi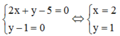 
Đúng 0
Bình luận (0)
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
(
x
-
3
)
+...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y
Tìm giá trị P m a x của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
