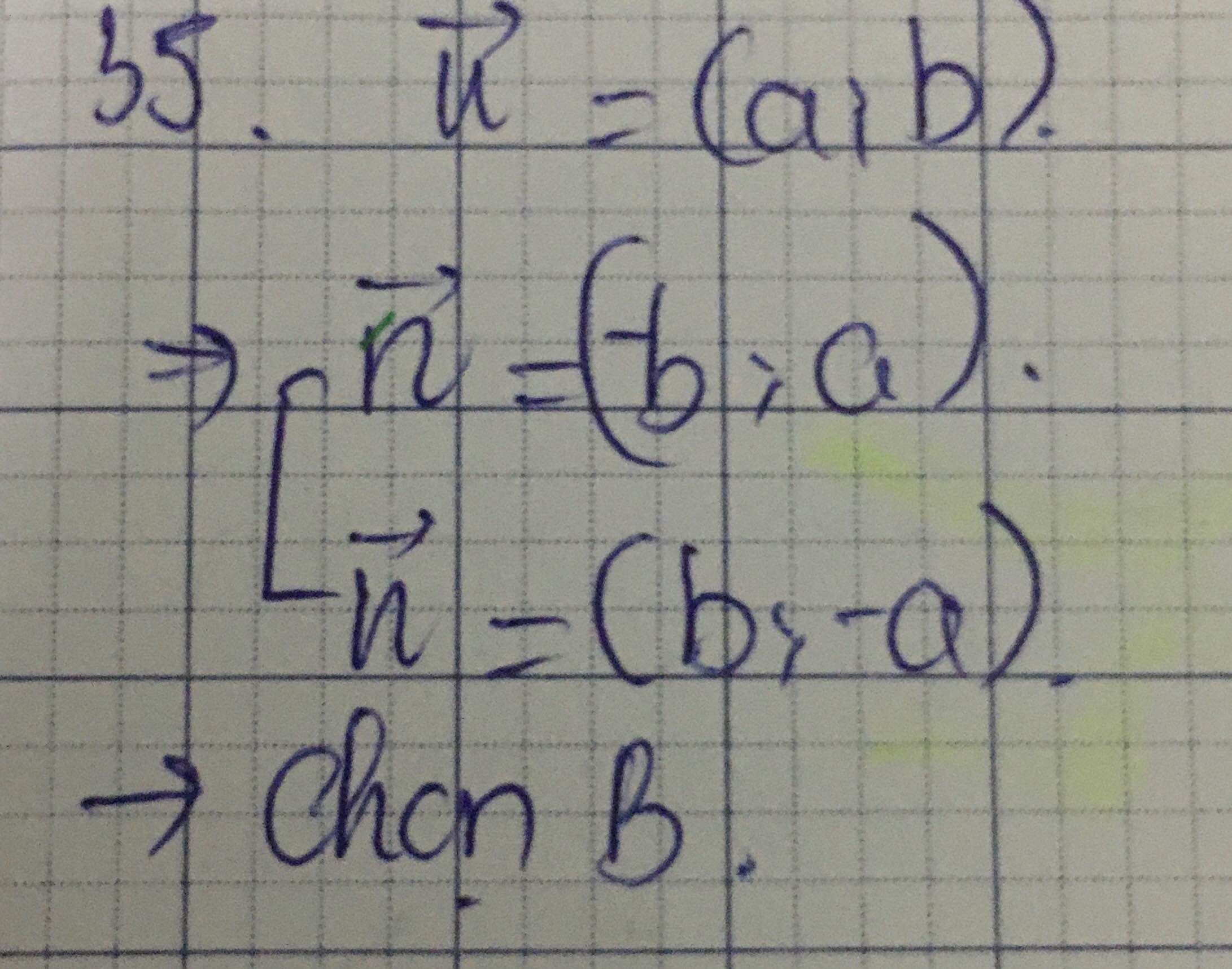Câu 32, 33, 34
Đọc tiếp
Câu 32, 33, 34 
Những câu hỏi liên quan
câu 31 câu 32 câu 33 câu 34 câu 35
Đọc tiếp
câu 31
câu 32
câu 33
câu 34
câu 35
Câu 31: A
Câu 32: C
Câu 33: D
Câu 34: B
Câu 35: C
Đúng 1
Bình luận (0)
Câu 32 , 33 , 34
32.
d có 1 vtpt là \(\left(2;-3\right)\) nên cũng nhận các vecto có dạng \(k\left(2;-3\right)\) là vecto pháp tuyến (k khác 0)
Thay \(k=-2\) ta được \(\left(-4;6\right)\) nên C đúng
33. Câu này chỉ có điểm A, ko có điểm M, chắc đề bài ghi sai
Đường thẳng vuông góc d nên nhận (1;-1) là 1 vtpt
Phương trình:
\(1\left(x-1\right)-1\left(y-0\right)=0\Leftrightarrow x-y-1=0\)
34.
Câu này cũng sai luôn, chỉ có C, D chứ ko có 2 điểm AB nào hết????"
\(\overrightarrow{CD}=\left(-1;5\right)\) nên đường thẳng nhận (-1;5) là 1 vtcp
Phương trình: \(\left\{{}\begin{matrix}x=-t\\y=3+5t\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Câu 8. Cho: 𝐵 3 + 32 + 33 + 34 + ⋯ + 3300 Chứng minh 𝐵 ⋮ 39
Đọc tiếp
Câu 8. Cho:
𝐵 = 3 + 32 + 33 + 34 + ⋯ + 3300
Chứng minh 𝐵 ⋮ 39
\(B=3+3^2+3^3+...+3^{300}\)
\(B=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{298}+3^{299}+3^{300}\right)\)
\(B=\left(3+3^2+3^3\right)+3^3\cdot\left(3+3^2+3^3\right)+...+3^{297}\cdot\left(3+3^2+3^3\right)\)
\(B=39+3^3\cdot39+...+3^{297}\cdot39\)
\(B=39\cdot\left(1+3^3+...+3^{297}\right)\)
Vậy B chia hết cho 39
Đúng 3
Bình luận (0)
Hình chóp S.ABC có 4 mặt là những tam giác đều bằng nhau . H là tâm đường tròn ngoại tiếp tam giác đều ABC , bán kính HC R √3(cm) . Biết rằng AB R √3 ,tính diện tích xung quanh của hình chóp
Đọc tiếp
Hình chóp S.ABC có 4 mặt là những tam giác đều bằng nhau . H là tâm đường tròn ngoại tiếp tam giác đều ABC , bán kính HC = R = √3(cm) . Biết rằng AB = R √3 ,tính diện tích xung quanh của hình chóp
\(R=\sqrt{3}\)
\(AB=R\sqrt{3}=3\)
Có các mặt là tam giác đều
\(\Rightarrow SC=AB=BC=AC=3\)
\(H\) là tâm đường tròn ngoại tiếp đồng thời là chân đường cao :
\(\Rightarrow\Delta SHC\)vuông tại \(H\)
Áp dụng vào tam giác SHC định lý py-ta- go
\(\Rightarrow SH=\sqrt{SC^2-HC^2}=\sqrt{6}cm\)
\(S_{ABC}=\frac{1}{2}.AC.AB.sin\widehat{A}=\frac{1}{2}.3.3.\frac{\sqrt{3}}{2}=\frac{9\sqrt{3}}{4}\)
\(\Rightarrow S\)xung quanh hình chóp \(=4S_{ABC}=9\sqrt{3}\left(cm^2\right)\)
Câu hỏi của Chu Hà Gia Khánh - Tiếng Anh lớp 4 - Học trực tuyến OLM
12 tháng 12 2021 lúc 7:01
Cho một điểm P thuộc miền trong của hình chữ nhật ABCD. Chứng minh rằng: Tổng diện tích hai hình vuông với độ dài cạnh lần lượt là khoảng cách từ điểm P đến hai đỉnh đối nhau bằng tổng diện tích hai hình vuông với các cạnh lần lượt là khoảng cách từ điểm P đến hai đỉnh đối còn lại.
Z=32+32+33+34+...+3100
tim Z
Z=31+32+33+34+...+3100
3Z=3.(31+32+33+34+...+3100)
3Z=3.31+3.32+3.33+...+3.3100
3Z=32+33+34+...+3101
Lấy 3Z= 32+33+34+...+3101
-
Z=31+32+33+34+...+3100
------------------------------------------- 2Z=3^101-3 =>Z=(3^101-3):2 Chú thích: ^ là mũ, cái phần đặt tính thì bạn để các số bằng nhau thẳng hàng nhé
Đúng 0
Bình luận (0)
So sánh: 31/32+32/33+35/34 và 31+32+35/34
Giúp mình với nha. Thanks nhìu
ta có: \(\frac{31+32+35}{34}=\frac{31}{34}+\frac{32}{34}+\frac{35}{34}.\)
mà \(\frac{31}{32}>\frac{31}{34};\frac{32}{33}>\frac{32}{34}\)
\(\Rightarrow\frac{31}{32}+\frac{32}{33}+\frac{35}{34}>\frac{31}{34}+\frac{32}{34}+\frac{35}{34}=\frac{31+32+35}{34}\)
Đúng 0
Bình luận (0)
26 tháng 3 2023 lúc 9:46
Điền dấu thích hợp vào chỗ chấm: 32/33 … 33/34
`32/33 ..... 33/34`
`(32xx34)/(33xx34) ..... (33xx33)/(33xx34)`
`1088/1122 ..... 1089/1122`
`-> 1088/1122 > 1089/1122`
`-> 32/33 > 33/34`
Đúng 4
Bình luận (0)
3233.....33343233.....3334
32×3433×34 .....33×3333×3432×3433×34 .....33×3333×34
10881122 .....1089112210881122 .....10891122
→ 10881122> 10891122→ 10881122> 10891122
→3233>3334
Đúng 0
Bình luận (10)
32 , 33, 34 ,35
