cho tứ giác abcd gọi a' b' c' d' lần lượt là trọng tâm bcd;acd;abd,abc. chứng minh rằng các đường thẳng aa';bb';cc' đồng qui

Những câu hỏi liên quan
Cho tứ giác ABCD. Gọi A',B',C',D' lần lượt là trọng tâm của các tam giác BCD,ACD,ABD,ABC. Chứng minh AA',BB',CC',DD' đồng quy
a) G là trọng tâm của ABCD <=> vtGA + vtGB + vtGC + vtGD = vt0 (1*)
A' là trọng tâm của BCD <=> vtA'B + vtA'C + vtA'D = vt0
<=> 3.vtA'G + vtGB + vtGC + vtGD = vt0 (2*) (chen điểm G vào biểu thức trên)
lấy (1*) - (2*): vtGA - 3.vtA'G = vt0 <=> vtGA = 3.vtA'G
đẳng thức này chứng tỏ vtGA và vtA'G cùng hướng => G nằm trên đoạn AA'
tương tự có B' là trọng tâm của ACD <=> 3.vtB'G + vtGA + vtGC + vtGD = vt0 (3*)
lấy (1*) - (3*): vtGB - 3vtB'G = vt0 <=> vtGB = 3vtB'G
=> G nằm trên đoạn BB'
tiếp tục cho 2 phần còn lại
=> G là điểm chung của các đoạn AA', BB', CC', DD'
b) từ biểu thức trên có: vtGA = -3.vtGA'
=> G chia đoạn AA' theo tỉ số k = -3
các đoạn kia tương tự đều cùng tỉ số k = -3
c) từ cm trên ta có:
vtGA = -3vtGA'
vtGB = -3vtGB'
vtGC = -3vtGC'
vtGD = -3vtGD'
=> vtGA+vtGB+vtGC+vtGD+vtGD = -3(vtGA'+vtGB'+vtGC'+vtGD') (**)
mà G là trọng tâm của ABCD nên vtGA+vtGB+vtGC+vtGD = vt0
(**) => vtGA'+vtGB'+vtGC'+vtGD' = vt0 => G là trọng tâm của A'B'C'D'
Đúng 1
Bình luận (0)
Cho tứ diện ABCD có thể tích là V. Gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Tính thể tích khối tứ diện A'B'C'D' theo V.
Cho tứ diện ABCD. Gọi A,B,C lần lượt là trọng tâm các tam giác BCD, ACD, ABD. Đặt
A
A
→
a
→
,
B
B
→
b
→
,
C
C...
Đọc tiếp
Cho tứ diện ABCD. Gọi A,B',C' lần lượt là trọng tâm các tam giác BCD, ACD, ABD. Đặt A A ' → = a → , B B ' → = b → , C C ' → = c → . Mệnh đề nào sau đây đúng?
![]()
![]()
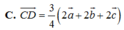
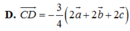
Cho tứ giác lồi ABCD, gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC và M, N lần lượt là trung điểm của các đoạn thẳng AC, BD. Chứng minh rằng các đường thẳng AA', BB', CC', DD' và MN đồng quy.
Gọi P và Q lần lượt là trung điểm của AC' và CA'.
CC' giao MN tại I
Xét tam giác AC'C. P là trung điểm AC', M là trung điểm của AC
=> PM là đường trung bình tam giác AC'C => PM//CC'
hay C'I//PM
C' là trọng tâm tam giác ABD => C'N=AN/3.(T/c trọng tâm)
Mà P là trung điểm AC' => C' là trung điểm PN.
Xét tam giác PNM: C' là trung điểm PN, C'I//PM => I là trung điểm của MN
=> CC' đi qua trung điểm của MN (1)
Tương tự ta chứng minh được AA' đi qua trung điểm MN (2)
Tương tự xét trong tam giác DMB: BB' và DD' cùng đi qua trung điểm I của MN (3)
Từ (1),(2) và (3) => AA';BB';CC';DD',MN đồng quy (đpcm).
Đúng 0
Bình luận (1)
Cho tứ giác ABCD. Gọi A` , B`, C` , D` lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Gọi E, F lần lượt là trung điểm của AC, BD
a, Chứng minh AA` đi qua trung điểm EF
b, Chứng minh 4 đường thẳng AA`, BB`, CC`, CC` đồng quy
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là
G
1
,
G
2
. Diện tích thiết diện đó bằng: A.
a
2
3
6
B.
2
a
2
3...
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là G 1 , G 2 . Diện tích thiết diện đó bằng:
A. a 2 3 6
B. 2 a 2 3 3
C. a 2 2 4
D. a 2 2 6
BI = (a√3)/2 (đường cao tam giác đều)
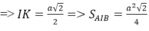
Đáp án C
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là
G
1
,
G
2
. Chu vi thiết diện đó bằng: A.
a
3
+
1
B.
a
2
3...
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là G 1 , G 2 . Chu vi thiết diện đó bằng:
A. a 3 + 1
B. a 2 3 + 1 2
C. 2 a 3 + 1
D. 2 a 3 + 3 2
Chu vi ∆ABI = AB + 2AI = a + 2.(a√3)/2 = a(1 + √3)
Đáp án A
Đúng 0
Bình luận (0)
Cho khối tứ diện đều ABCD cạnh bằng a. Gọi A', B', C', D' lần lượt là trọng tâm của tam giác BCD, ADC, DAB, ABC
a) Chứng minh A'B'C'D' cũng là khối tứ diện đều
b) Tính \(V_{A'B'C'D'}\) theo a

nên \(V_{A'B'C'D'}=\dfrac{1}{27}V_{ABCD}=\dfrac{\sqrt{2}}{324}a^2\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng:
A. Qua M và song song với AB
B. Qua N và song song với BD
C. Qua G và song song với CD
D. Qua G và song song với BC
Chọn đáp án C
Ta có: MN là đường trung bình tam giác ACD.
=> CD // MN CD // (MNG)
Mặt khác: ![]()
Khi đó: Giao tuyến = ![]() = Gx // CD
= Gx // CD
Đúng 0
Bình luận (0)













