Chọn đáp án C
Ta có: MN là đường trung bình tam giác ACD.
=> CD // MN CD // (MNG)
Mặt khác: ![]()
Khi đó: Giao tuyến = ![]() = Gx // CD
= Gx // CD
Chọn đáp án C
Ta có: MN là đường trung bình tam giác ACD.
=> CD // MN CD // (MNG)
Mặt khác: ![]()
Khi đó: Giao tuyến = ![]() = Gx // CD
= Gx // CD
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB = 2. Xét M là điểm thay đổi trên cạnh BC. Mặt phẳng α qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức S = M P 2 + N Q 2 bằng
![]()
![]()
![]()
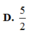
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AC = a 2 , biết SA vuông góc với mặt đáy, SA = a. Gọi G là trọng tâm của tam giác SBC, là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC.
A. V = 4 9 a 3
B. V = 2 27 a 3
C. V = 5 27 a 3
D. V = 5 54 a 3
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, A C = a 2 . SA vuông góc với mặt phẳng (ABC) và SA=a. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B' và C'. Thể tích khối chóp S.A'B'C' bằng:
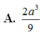
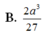
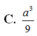
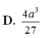
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, AC=a 2 , SA ⊥ (ABC), SA=a. Gọi G là trọng tâm tam giác SBC, mặt phẳng ( α ) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, A C = a 2 , S A ⊥ m p A B C , S A = a . Gọi G là trọng tâm tam giác SBC, mặt phẳng α đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN?
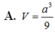
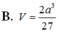
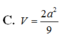
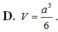
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp α qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của α với BD và AD. Xét các mệnh đề sau:
(1) MP // BC
(2) MQ // AC
(3) PQ // AI
(4) (MPQ) // (ABC)
Số mệnh đề đúng là:
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng α song song với mặt phẳng (SBC), cắt các cạnh CD, DS, SA lần lượt tại các điểm N, P, Q. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là
A. Một đường thẳng.
B. Nửa đường thẳng.
C. Đoạn thẳng song song với AB.
D. Tập hợp rỗng.
Cho tứ diện A B C D , G là trọng tâm ∆ A B D và M là điểm trên cạnh BC sao cho B M = 2 M C . Đường thẳng MG song song với mặt phẳng
![]()
![]()
![]()
Cho tứ diện ABCD. Điểm M thuộc đoạn AC M (khác A M, khác C). Mặt phẳng ( α ) đi qua M song song với AB và AD. Thiết diện của với tứ diện ABCD là hình gì?
A. Hình tam giác.
B. Hình bình hành.
C. Hình vuông
D. Hình chữ nhật.