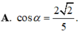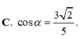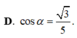Các câu hỏi tương tự
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB 2. Xét M là điểm thay đổi trên cạnh BC. Mặt phẳng
α
qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức
S
M
P
2
+
N
Q
2
bằng
Đọc tiếp
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB = 2. Xét M là điểm thay đổi trên cạnh BC. Mặt phẳng α qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức S = M P 2 + N Q 2 bằng
![]()
![]()
![]()
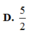
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng
α
song song với mặt phẳng (SBC), cắt các cạnh CD, DS, SA lần lượt tại các điểm N, P, Q. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là A. Một đường thẳng. B. Nửa đường thẳng. C. Đoạn thẳng song song với AB. D. Tập hợp rỗng.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng α song song với mặt phẳng (SBC), cắt các cạnh CD, DS, SA lần lượt tại các điểm N, P, Q. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là
A. Một đường thẳng.
B. Nửa đường thẳng.
C. Đoạn thẳng song song với AB.
D. Tập hợp rỗng.
1.Cho lăng trụ tam giác ABC.ABC có ∆ABC vuông cân tại B. Gọi O,O lần lượt là các điểm trên BA,BC sao cho BO/BABO/BC1/3.mệnh đề nào sau đây là đúng?
A.OO vuông góc BB
B.OO vuông góc BM, với M là trung điểm của AC.
C.Ô vuông góc BC.
D.Ô vuông góc AB.
2.Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm Ở, SA vuông góc (ABCD), SAABa.Gọi (Q) là mặt phẳng qua SA vuông góc với (SBD).Thiết diện của hình chóp S.ABCD cắt bởi (Q) là
A.tam giác vuông
B.tam giác đều
C.tam giác vuông cân
D.hình bình hành
3.C...
Đọc tiếp
1.Cho lăng trụ tam giác ABC.A'B'C' có ∆ABC vuông cân tại B. Gọi O,O' lần lượt là các điểm trên BA',BC' sao cho BO/BA'=BO'/BC'=1/3.mệnh đề nào sau đây là đúng? A.OO' vuông góc BB' B.OO' vuông góc BM, với M là trung điểm của AC. C.Ô' vuông góc BC'. D.Ô' vuông góc A'B'. 2.Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm Ở, SA vuông góc (ABCD), SA=AB=a.Gọi (Q) là mặt phẳng qua SA vuông góc với (SBD).Thiết diện của hình chóp S.ABCD cắt bởi (Q) là A.tam giác vuông B.tam giác đều C.tam giác vuông cân D.hình bình hành 3.Cho hình chóp tam giác đều,các cạnh bên có độ dài bằng a√3 và tạo với đáy một góc 60°.Diện tích S của đáy hình chóp là A.a²√3/9 B.27a²√3/16 C.9a²√3/16 D.3a²√3/16 4.Cho hình chóp S.ABCD có đường cao SA=4a.Biết đáy ABCD là hình thang vuông tại A và B với AB=BC'=3a,AD=a.Gọi M là trung điểm của cạnh AB và (a) là mặt phẳng quá M và vuông góc với AB.Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (a) là đa giác có diện tích bằng A.5a²/2 B.7a²/2 C.7a² D.5a² 5.Cho tứ diện đều ABCD.Thiết diện của tứ diện ABCD và mặt phẳng trungg trực của cạnh BC là A.hình tháng B.tam giác vuông C.hình bình hành D.tam giác cân 6.Chi hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SB=a,SA=a√3 và SA vuông góc (ABC).Gọi M là điểm trên cạnh AB và AM=x(0
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi
α
là số đo của góc giữa hai đường thẳng MG và NP. Khi đó
cos
α
bằng
Đọc tiếp
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai đường thẳng MG và NP. Khi đó cos α bằng
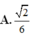
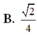
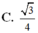
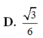
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK). A. Điểm I B. Điểm E C. Điểm F D. Điểm K
Đọc tiếp
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK= 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK).
A. Điểm I
B. Điểm E
C. Điểm F
D. Điểm K
Cho tứ diện ABCD có DA vuông góc với mp(ABC),
A
D
A
B
B
C
a
,
D
B
⊥
B
C
. Kí hiệu
V
1
,
V
2
,
V
3
lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi...
Đọc tiếp
Cho tứ diện ABCD có DA vuông góc với mp(ABC), A D = A B = B C = a , D B ⊥ B C . Kí hiệu V 1 , V 2 , V 3 lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi quay quanh BC. Trong các mệnh đề sau, mệnh đề nào đúng ?
![]()
![]()
![]()
![]()
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng:
AB
→
-
C
D
→
A
C
→
B
D
→
2
P
Q
→
Đọc tiếp
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng: AB → - C D → = A C → B D → = 2 P Q →
Cho hình chóp đều S.ABCD có đáy và cạnh bên đều bằng 2. Gọi O là tâm đáy, M và N lần lượt là trung điểm của OA và SO. Xét mặt phẳng
α
chứa đường thẳng MN và song song với đường thẳng BD. Diện tích của thiết diện tạo bởi
α
và hình chóp bằng
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy và cạnh bên đều bằng 2. Gọi O là tâm đáy, M và N lần lượt là trung điểm của OA và SO. Xét mặt phẳng α chứa đường thẳng MN và song song với đường thẳng BD. Diện tích của thiết diện tạo bởi α và hình chóp bằng
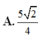
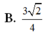
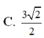
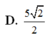
Cho hình chóp S.ABC có
S
A
⊥
m
p
(
A
B
C
)
,
S
A
4
α
5
,
A
B
A
C
α
,
B
C
6
α
5
. Gọi M là trung điểm của BC và
α
là góc g...
Đọc tiếp
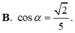
Cho hình chóp S.ABC có S A ⊥ m p ( A B C ) ,
S A = 4 α 5 ,
A B = A C = α , B C = 6 α 5 . Gọi M là trung điểm của BC và α là góc giữa hai đường thẳng AC, SM. Tính cos α