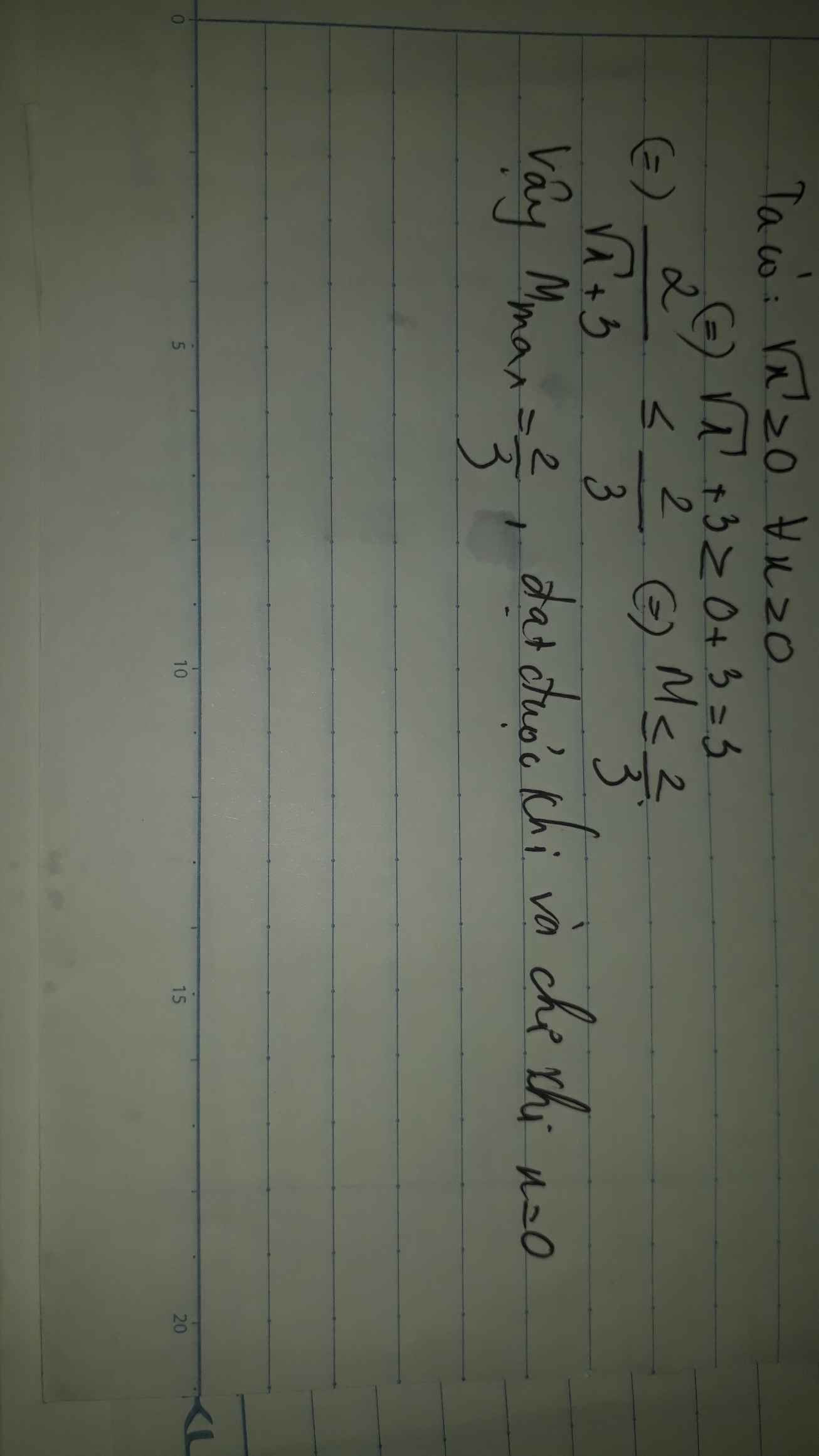ĐKXĐ:

 \(\sqrt{x-5}\ge0\Rightarrow x\ge5\)

\(\sqrt{7-x}\ge0\Rightarrow x\le7\)

=> P_max =2 tại x=7

DKXD:\(5\le x\le7\)

GTLN: \(P=\sqrt{x-5}+\sqrt{7-x}=1.\sqrt{x-5}+1.\sqrt{7-x}\)

                                  \(\le\frac{1^2+\left(\sqrt{x-5}\right)^2}{2}+\frac{1^2+\left(\sqrt{7-x}\right)^2}{2}\left(bdtCOSI\right)\)

                                    \(=\frac{2+x-5+7-x}{2}=2\)

                       "="\(\Leftrightarrow\hept{\begin{cases}1=\sqrt{x-5}\\1=\sqrt{7-x}\\7\ge x\ge5\end{cases}}\Leftrightarrow x=6\)

Vậy..............................................................

GTNN: ta sẽ chứng minh: \(P\ge\sqrt{2}\)

 bđt có thể viết lại thành:\(\sqrt{x-5}+\sqrt{7-x}\ge\sqrt{2}\Leftrightarrow\left(\sqrt{x-5}+\sqrt{7-x}\right)^2\ge\left(\sqrt{2}\right)^2\)

                                       \(\Leftrightarrow x-5+7-x+2\sqrt{\left(x-5\right)\left(7-x\right)}\ge2\Leftrightarrow2+2\sqrt{\left(x-5\right)\left(7-x\right)}\ge2\)

                                       \(\Leftrightarrow2\sqrt{\left(x-5\right)\left(7-x\right)}\ge0\)(đúng với mọi x thỏa mãn \(7\ge x\ge5\))

          "="\(\Leftrightarrow\hept{\begin{cases}2\sqrt{\left(x-5\right)\left(7-x\right)}\\7\ge x\ge5\end{cases}\Rightarrow\orbr{\begin{cases}x=5\\x=7\end{cases}}}\)

                      Vậy..........

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)

b: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)

\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)

\(=\dfrac{2}{x+\sqrt{x}+1}\)

c: Ta có: \(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ

\(\Leftrightarrow\dfrac{2}{x+\sqrt{x}+1}>0\forall x\)

1 ) \(A=\sqrt{x-2}+\sqrt{4-x}\)

ĐKXĐ : \(2\le x\le4\)

\(\Rightarrow A^2=x-2+4-x+2\sqrt{\left(x-2\right)\left(4-x\right)}=2+2\sqrt{\left(x-2\right)\left(4-x\right)}\)

Áp dụng bđt AM - GM ta có : 

\(2\sqrt{\left(x-2\right)\left(4-x\right)}\le x-2+4-x=2\)

\(\Rightarrow A^2\le2+2=4\Rightarrow-2\le A\le2\)

Mà A > 0 nên ko thể có min = - 2 nên \(2\le x\le4\) ta chọn x = 2

=> A = \(\sqrt{2}\)

Vậy \(\sqrt{2}\le A\le2\)

Ta có: \(A=\sqrt{x-1-2\sqrt{x-2}}-\sqrt{x+7-6\sqrt{x-2}}\)

\(=\sqrt{x-2-2\cdot\sqrt{x-2}\cdot1+1}-\sqrt{x-2-6\cdot\sqrt{x-2}+9}\)

\(=\sqrt{\left(\sqrt{x-2}-1\right)^2}-\sqrt{\left(\sqrt{x-2}-3\right)^2}=\left|\sqrt{x-2}-1\right|-\left|\sqrt{x-2}-3\right|\)

=>\(A\le\left|\sqrt{x-2}-1-\sqrt{x-2}+3\right|=2\forall x\) thỏa mãn ĐKXĐ

Dấu '=' xảy ra khi \(\left(\sqrt{x-2}-1\right)\left(\sqrt{x-2}-3\right)\ge0\)

=>\(\left[\begin{array}{l}\sqrt{x-2}\ge3\\ \sqrt{x-2}\le1\end{array}\right.\Rightarrow\left[\begin{array}{l}x-2\ge9\\ 0\le x-2\le1\end{array}\right.\Rightarrow\left[\begin{array}{l}x\ge11\\ 2\le x\le3\end{array}\right.\)

Ta có: \(x=9-4\sqrt{5}\)

⇔ \(\sqrt{x}=\sqrt{9-4\sqrt{5}}=\sqrt{5-4\sqrt{5}+4}\)

⇔ \(\sqrt{x}=\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}-2\right|\)

⇔ \(\sqrt{x}=\sqrt{5}-2\)   

Khi đó:    \(P=\dfrac{1-\sqrt{5}+2}{\sqrt{5}-2+2}=\dfrac{3-\sqrt{5}}{\sqrt{5}}\)

em tham khảo