chứng minh ADC đồng dạng vs BDH
Hoạc chứng minh IM.IC=2IE
Nêu hướng thôi cx đc
Cho 2 tứ giác ABCD VÀ XYZT sao cho 2 Tam giác ABD, XYT đồng dạng. Góc ABC= XYZ và góc ADC= XTZ. Chứng minh Tam giác BCD và YZT đồng dạng Chứng minh góc BAC=YXZ Chứng minh AC/BD= XZ/YT
a: Xét ΔBCD và ΔYZT có
góc DBC=góc TYZ
góc BCD=góc YZT
=>ΔBCD đồng dạng với ΔYZT
b: ΔBCD đồng dạng với ΔYZT
=>góc BDC=góc YTZ
=>góc BAC=góc YXZ
Cho tam giác ABC, ba đương cao AD,BE,CF. Gọi M,N,I,K lần lượt là hình chiếu của D trên AB;AC;BE;CF.
a) Chứng minh MI//EF;NK//EF
b) chứng minh tam giác AMD đông dạng với ADB, tam giác AND đồng dạng với ADC
c) Chứng minh M,N,I,K thằng hàng
Em cần gấp ạ. Ai biết giúp e với. E cũng không cần câu a và b. Chủ yếu cau c thôi ạ
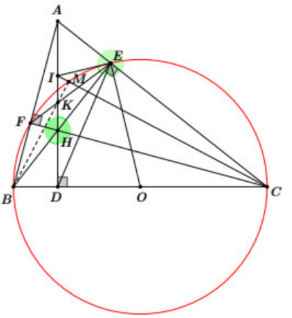
Cho tam giác ABC có 3 góc nhọn AD,BE,CF cắt H a) chứng minh tam giác AEF đồng dạng với tam giác ADC b) chứng minh tam giác ADE đồng dạng với tam giác ACH c) lấy điểm K đối xứng với E qua BC. Chứng minh K,D,F thẳng hàng
a: Sửa đề: ΔAEB
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
b: góc HDC+góc HEC=180 độ
=>HDCE nội tiếp
Xét ΔADE và ΔACH có
góc DAE chung
góc ADE=góc ACH
=>ΔADE đồng dạng với ΔACH
Cho tam giác ABC có các đường cao AD,BE,CF cắt nhau tại H
a) Chứng minh: tam giác BEC đồng dạng tam giác ADC
b) Chứng minh: AH.HD = BH.HE
c) Chứng minh: tam giác CDE đồng dạng tam giác CAB
d) Gọi N là giao điểm của EF và AD. Chứng minh rằng FC là tia phân giác của góc DFE. Từ đó suy ra NH.AD = AN.HD
Vào TK mk nhá ! Nguồn h o c 2 4 270264



Cho
cân tại A (AB=AC). Gọi H là trung điểm BC, M là trung điểm AC
Chứng minh tứ giác ABHM là hình thang.
Gọi E là điểm đối xứng H qua M. Chứng minh tứ giác AECH là hình chữ nhật.
Gọi I là trung điểm AH. Chứng minh B, I, E thẳng hàng.
Làm câu c thôi cx đc ạ.
a: Xét ΔABC có
M là trung điểm của AC
H là trung điểm của bC
Do đó: MH là đường trung bình của ΔABC
Suy ra: MH//AB
hay ABHM là hình thang
Cho tam giác cân ABC (AB=AC), các đường cao AD; BE; CF cắt nhau tại H
a) Chứng minh tam giác ADC đồng dạng với tam giác BEC
b) Chứng minh AB.CE=BC.BD
CHo tam giác ABC phân giác AD . TRên nửa mặt phẳng bờ BC không chứa Điểm A vẽ tia Bx sao cho góc BCx = góc BAD . GỌi I là giao điểm của tia Cx với AD kéo dài .
a) Hai tam giác ADC và BDI có đồng dạng không . VÌ sao ?
b) Chứng minh AB.AC=AD.AI
c) CHứng minh AB.AC-DB.DC=AD2
Bài giải
a,
\(\widehat{DAC}=\widehat{BAD}=\widehat{DBI}\)( AD là tia phân giác \(\widehat{BAC}\) )
\(\widehat{ADC}=\widehat{BDI}\)
\(\Rightarrow\Delta ADC\sim\Delta BDI\left(g.g\right)\)
b, \(\Delta ADC\sim\Delta BDI\left(cmt\right)\Rightarrow\widehat{AIB}=\widehat{ACD}\)
\(\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABI\sim\Delta ADC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AI}=\dfrac{AD}{AC}\Rightarrow AB.AC=AD.AI\)
Cho ∆ABC vuông tại A (AC > AB), trên cạnh AC lấy điểm D. Kẻ tia Cx vuông góc với
BD tại E.
a) Chứng minh ∆ABD đồng dạng với ∆ECD
b) Chứng minh góc BEA = góc BCA
c) Từ A kẻ đường thẳng vuông góc với AE cắt BE tại I. Chứng minh: AB.CE = BI.AC
d) Chứng minh AB.CE + AE.BC = AC.BE

chứng minh đồng dạng giúp mik vs
Xét tam giác CMH và tam giác CAD có
góc C chung
góc CHM = góc CAH = 90
=> đồng dạng