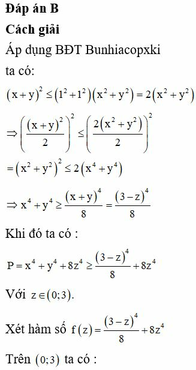\(x\left(x-z\right)+y\left(y-z\right)=0\)\(\Leftrightarrow\)\(x^2+y^2=z\left(x+y\right)\)

\(\frac{x^3}{z^2+x^2}=x-\frac{z^2x}{z^2+x^2}\ge x-\frac{z^2x}{2zx}=x-\frac{z}{2}\)

\(\frac{y^3}{y^2+z^2}=y-\frac{yz^2}{y^2+z^2}\ge y-\frac{yz^2}{2yz}=y-\frac{z}{2}\)

\(\frac{x^2+y^2+4}{x+y}=\frac{z\left(x+y\right)+4}{x+y}=z-x-y+\frac{4}{x+y}+x+y\ge z-x-y+4\)

Cộng lại ra minP=4, dấu "=" xảy ra khi \(x=y=z=1\)

\(x,y,z>0\)

Áp dụng BĐT Caushy cho 3 số ta có:

\(x^3+y^3+z^3\ge3\sqrt[3]{x^3y^3z^3}=3xyz\ge3.1=3\)

\(P=\dfrac{x^3-1}{x^2+y+z}+\dfrac{y^3-1}{x+y^2+z}+\dfrac{z^3-1}{x+y+z^2}\)

\(=\dfrac{\left(x^3-1\right)^2}{\left(x^2+y+z\right)\left(x^3-1\right)}+\dfrac{\left(y^3-1\right)^2}{\left(x+y^2+z\right)\left(y^3-1\right)}+\dfrac{\left(z^3-1\right)^2}{\left(x+y+z^2\right)\left(x^3-1\right)}\)

Áp dụng BĐT Caushy-Schwarz ta có:

\(P\ge\dfrac{\left(x^3+y^3+z^3-3\right)^2}{\left(x^2+y+z\right)\left(x^3-1\right)+\left(x+y^2+z\right)\left(y^3-1\right)+\left(x+y^2+z\right)\left(y^3-1\right)}\)

\(\ge\dfrac{\left(3-3\right)^2}{\left(x^2+y+z\right)\left(x^3-1\right)+\left(x+y^2+z\right)\left(y^3-1\right)+\left(x+y^2+z\right)\left(y^3-1\right)}=0\)

\(P=0\Leftrightarrow x=y=z=1\)

Vậy \(P_{min}=0\)

Câu 1: xy + x - y = 4

<=> (xy + x) - (y+ 1) = 3

<=> x(y+1) - (y + 1) = 3

<=> (y + 1) (x - 1) = 3

Theo bài ra cần tìm các số nguyên dương x, y => Xét các trường hợp y + 1 nguyên dương và x -1 nguyên dương.

Mà 3 = 1 x 3 => Chỉ có thể xảy ra các trường hợp sau:

* TH1: y + 1 = 1; x - 1 = 3 => y = 0; x = 4 (loại vì y = 0)

* TH2: y + 1 = 3; x -1 = 1 => y = 2; x = 2 (t/m)

Vậy x = y = 2.

Câu 2:

Ta có:

 (a - b)/x = (b-c)/y = (c-a)/z =(a-b + b -c + c - a) (x + y + z) = 0

Vì x; y; z nguyên dương => a-b =0; b - c = 0; c- a =0 => a = b = c

 \(\frac{a-b}{x}=\frac{b-c}{y}=\frac{c-a}{z}\)

Ta sẽ c/m: \(\frac{x}{x+1}\le\frac{9}{16}x+\frac{1}{16}\)

\(\Leftrightarrow\frac{x}{x+1}-\frac{9}{16}x-\frac{1}{16}\le0\)

\(\Leftrightarrow\frac{-\left(3x-1\right)^2}{16\left(x+1\right)}\le0\) (đúng)

Thiết lập tương tự hai BĐT còn lại và cộng theo vế ta được: \(Q\le\frac{9}{16}\left(x+y+z\right)+\frac{3}{16}=\frac{9}{16}+\frac{3}{16}=\frac{3}{4}\)

Vậy Q max = ³/₄ khi x = y  =z  =¹/₃

sao lại viết thế kia

học tốt nha

Cách tth_new UCT khá gọn nhưng t có cách đẹp không kém :))

\(3-Q=\left(1-\frac{x}{x+1}\right)+\left(1-\frac{y}{y+1}\right)+\left(1-\frac{z}{z+1}\right)\)

\(=\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}\)

\(\ge\frac{9}{x+y+z+3}=\frac{9}{4}\)

\(\Rightarrow Q\le\frac{3}{4}\)

Đẳng thức xảy ra tại x=y=z=¹/₃

Ta thấy 
72
=
2
3
.
3
2
72=2 
3
 .3 
2
  nên a, b có dạng 
{
�
=
2
�
3
�
�
=
2
�
.
3
�
{ 
a=2 
x
 3 
y
 
b=2 
z
 .3 
t
 
​
  với 
�
,
�
,
�
,
�
∈
N
x,y,z,t∈N và 
�
�
�
{
�
,
�
}
=
3
;
�
�
�
{
�
,
�
}
=
2
max{x,z}=3;max{y,t}=2. 

 Theo đề bài, ta có 
2
�
.
3
�
+
2
�
.
3
�
=
42
2 
x
 .3 
y
 +2 
z
 .3 
t
 =42

 
⇔
2
�
−
1
.
3
�
−
1
+
2
�
−
1
3
�
−
1
=
7
⇔2 
x−1
 .3 
y−1
 +2 
z−1
 3 
t−1
 =7   (*), do đó 
�
,
�
,
�
,
�
≥
1
x,y,z,t≥1

 TH1: 
�
≥
�
,
�
≤
�
x≥z,y≤t. Khi đó 
�
=
3
,
�
=
2
x=3,t=2. (*) thành:

 
4.
3
�
−
1
+
3.
2
�
−
1
=
7
4.3 
y−1
 +3.2 
z−1
 =7 
⇔
�
=
�
=
1
⇔y=z=1

 Vậy 
{
�
=
24
�
=
18
{ 
a=24
b=18
​
  (nhận)

 TH2: KMTQ thì giả sử 
�
≥
�
,
�
≥
�
x≥z,y≥t. Khi đó 
�
=
3
,
�
=
2
x=3,z=2. (*) thành 

 
4.
3
�
−
1
+
2.
3
�
−
1
=
7
4.3 
y−1
 +2.3 
t−1
 =7, điều này là vô lí.

 Vậy 
(
�
,
�
)
=
(
24
,
18
)
(a,b)=(24,18) hay 
(
18
,
24
)
(18,24) là cặp số duy nhất thỏa yêu cầu bài toán.

voi x,y,z>0 ta co

ap dung bdt co si ta co

\(T>=3\sqrt[3]{\sqrt{\left(\frac{x^2+1}{x^2}+\frac{1}{y^2}\right)\left(\frac{y^2+1}{y^2}+\frac{1}{z^2}\right)\left(\frac{z^2+1}{z^2}+\frac{1}{x^2}\right)}}\)

=\(3\sqrt[3]{\sqrt{\left(1+\frac{1}{x^2}+\frac{1}{y^2}\right)\left(1+\frac{1}{y^2}+\frac{1}{z^2}\right)\left(1+\frac{1}{z^2}+\frac{1}{x^2}\right)}}\)

>=\(3\sqrt[3]{\sqrt{3\sqrt[3]{\frac{1}{x^2y^2}}.3\sqrt[3]{\frac{1}{y^2z^2}}.3\sqrt[3]{\frac{1}{x^2z^2}}}}=3\sqrt[3]{\sqrt{27\sqrt[3]{\frac{1}{\left(xyz\right)^4}}}}\)

=\(3\sqrt[3]{\sqrt{27.\frac{1}{xyz}.\sqrt[3]{\frac{1}{xyz}}}}=3\sqrt{3}.\sqrt[9]{\frac{1}{\left(xyz\right)^2}}\)

ap dung bdt co si ta co 

\(x+y+z>=3\sqrt[3]{xyz}\)

<=>3>=\(3\sqrt[3]{xyz}\left(dox+y+z=3\right)\)

<=>xyz<=1

<=>1/xyz>=1

<=>\(\sqrt[9]{\frac{1}{\left(xyz\right)^2}}>=1\)

do do T>=\(3\sqrt{3}\)

dau = xay ra <=>x=y=z=1

\(P=\frac{1}{x\left(x+1\right)}+\frac{1}{y\left(y+1\right)}+\frac{1}{z\left(z+1\right)}\)

\(\ge3\sqrt[3]{\frac{1}{xyz\left(x+1\right)\left(y+1\right)\left(z+1\right)}}\)

Mà theo BĐT AM - GM ta có tiếp:

\(xyz\le\left(\frac{x+y+z}{3}\right)^3=1\)

\(\left(x+1\right)\left(y+1\right)\left(z+1\right)\le\left(\frac{x+y+z+3}{3}\right)^3=8\)

\(\Rightarrow P\le\frac{3}{2}\)

Đẳng thức xảy ra tại x=y=z=1

Vậy..................