thể tích của một hình chóp đều là 126cm3,chiều cao hình chóp là 6cm.tính diện tích của nó

Những câu hỏi liên quan
thể tích của một hình chóp đều là 126cm3,chiều cao hình chóp là 6cm.tính diện tích của nó
- Tính diện tích mặt đáy từ công thức: V=1/3. Sđ. h
- Tính độ dài cạnh mặt đáy: Sđ = a^2 => a= \(\sqrt{Sđ}\)
- Vì là hình c/đều nên mặt bên là t/giác đều => Cạnh mặt đáy bằng cạnh bên và trung tuyến cũng là đường cao, vẽ đường trung tuyến của mặt bên, tính 1/2 cạnh mặt đáy.
- Áp dụng Py-ta-go tính đường cao vừa vẽ theo công thức :
BC^2=AB^2+AC^2
- tính diện tích mặt bên nhân với 4 + với dt đáy ra diện tích hình chóp cần tìm.
Đúng 0
Bình luận (0)
Thể tích hình chóp đều bằng 126cm3, chiều cao của nó là 6 cm. Diện tích đáy hình chóp là:
A. 45 cm2;
B.60 cm2;
C. 52 cm2;
D. 63 cm2.
Thể tích hình chóp đều bằng 126cm3, chiều cao của nó là 6 cm. Diện tích đáy hình chóp là:
A. 45 cm2;
B.60 cm2;
C. 52 cm2;
D. 63 cm2.
thể tích của một hình chóp đều là 126cm3, chiều cao hình chóp là 6cm. tính diện tích đáy của nó.
- Tính diện tích mặt đáy từ công thức: V=1/3. Sđ. h
- Tính độ dài cạnh mặt đáy: Sđ = a^2 => a= √Sđ
- Vì là hình c/đều nên mặt bên là t/giác đều => Cạnh mặt đáy bằng cạnh bên và trung tuyến cũng là đường cao, vẽ đường trung tuyến của mặt bên, tính 1/2 cạnh mặt đáy.
- Áp dụng Py-ta-go tính đường cao vừa vẽ theo công thức :
BC^2=AB^2+AC^2
- tính diện tích mặt bên nhân với 4 + với dt đáy ra diện tích hình chóp cần tìm.
Đúng 0
Bình luận (0)
Thể tích của một hình chóp đều là 126cm^3, chiều cao hình chóp là 6cm. Tính diện tích đáy của nó (giải đầy đủ giúp e ạ)
Xem chi tiết
Lời giải:
Thể tích hình chóp = $\frac{1}{3}$ x diện tích đáy x chiều cao.
Do đó diện tích đáy là:
$126.3:6=63$ (cm2)
Đúng 1
Bình luận (0)
Thể tích của một hình chóp đều là1280cm3, chiều cao của hình chóp là 15 cm. Tính diện tích đáy hình chóp đó?
một hình chóp tứ giác đều có cạnh đáy 5cm, trung đoạn 6,5cm, chiều cao hình chóp là 6cm. tính diện tích xung quanh và thể tích của hình chóp tứ giác đều?
Sxq=5*4*6,5/2=65cm2
V=5^2*6=150cm3
Đúng 0
Bình luận (1)
Nữa chu vi đáy của hình chóp đều:
\(5\cdot4:2=10\left(cm\right)\)
Diện tích xung quanh của hình chóp đều là:
\(S_{xq}=10\cdot6,5=65\left(cm^2\right)\)
Diện tích đáy của hình chóp đều:
\(5^2=25\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot25\cdot6=50\left(cm^3\right)\)
Đúng 1
Bình luận (0)
Cho hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao của hình chóp là 4cm. Tính:
a) Diện tích xung quanh của hình chóp
b) Thể tích của hình chóp.
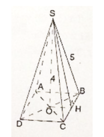
a) Ta có
OC2 = SC2 - SO2 (Pytago)
= 52 - 42 = 9(cm)
=> OC = 3(cm)
=> AC = 6(cm)
AB2 + BC2 = AC2 (pytago)
2BC2 = AC2 (do AB = BC)
BC2 = AC2/2 = 36/2 = 18(cm)
BC = √18 = 3√2 (cm)
Gọi K là trung điểm của BC. Tam giác SBC cân tại S có SH là đường trung tuyến nên SH cũng là đường cao. Suy ra SH ⊥ BC
Do đó
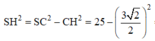
![]()

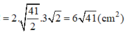
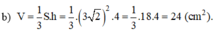
Đúng 0
Bình luận (0)














