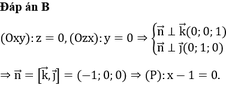Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho ba điểm I(1;1) J(-2;2) K(2;-2).Tìm tọa độ các đỉnh của hình vuông ABCD sao cho I là tâm hình vuông, J thuộc cạnh AB và K thuộc cạnh CD.

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho điểm
M
2
;
−
1
;
1
. Tìm tọa độ điểm M¢ là hình chiếu vuông góc của M trên mặt phẳng (Oxy) A.
M
2
;
−
1
;
0
B.
M
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M 2 ; − 1 ; 1 . Tìm tọa độ điểm M¢ là hình chiếu vuông góc của M trên mặt phẳng (Oxy)
A. M ' 2 ; − 1 ; 0
B. M ' 0 ; 0 ; 1
C. M ' − 2 ; 1 ; 0
D. M ' 2 ; 1 ; − 1
Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho điểm M(-1;1). Viết phương trình đường thẳng qua M và tạo với hai trục tọa độ một tam giác vuông cân.
Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho điểm M(-1;1). Viết phương trình đường thẳng qua M và tạo với hai trục tọa độ một tam giác vuông cân.
gọi Pt đường thảng .....y=ax+b(d)
d đi qua M(-1,1) 1=-a+b⇔b=a+1
gọi d cắt Ox tại \(A\left(-\dfrac{b}{a},O\right)\)
d cắt Oy tại \(B\left(O,b\right)\)
\(\Delta AOB\) vuông cân tại o
\(\Rightarrow OA=OB\Rightarrow\left(-\dfrac{b}{a}\right)^2+o^2=o^2+b^2\)
\(\dfrac{b^2}{a^2}=b^2\Leftrightarrow\dfrac{1}{a^2}=1\Leftrightarrow a^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=2\\b=0\left(loại\right)\end{matrix}\right.\)
(do d cắt 2 trục tọa độ nên a,b≠0)
vậy PtT đg thảng d:y=x+2
Đúng 0
Bình luận (0)
Gọi pt đường thẳng có dạng \(y=ax+b\)
Đường thẳng qua M tạo 2 trục tọa độ 1 tam giác vuông cân khi nó có hệ số góc \(a=1\) hoặc \(a=-1\)
\(\Rightarrow\left[{}\begin{matrix}y=x+b\\y=-x+b\end{matrix}\right.\)
Thay tọa độ M vào phương trình ta được:
\(\left[{}\begin{matrix}1=-1+b\\1=-\left(-1\right)+b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}b=2\\b=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=x+2\\y=-x\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là: A. H(2;0;4) B. H(0;-1;4) C. H(2;-1;0) D. H(0;-1;0).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:
A. H(2;0;4)
B. H(0;-1;4)
C. H(2;-1;0)
D. H(0;-1;0).
Đáp án C
Do chiếu xuống (Oxy) nên z=0 và x,y giữ nguyên.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, hình chiếu vuông góc của A(3;2;-1) trên mặt phẳng (Oxy) là điểm A. H(3;2;0) B. H(0;0;-1) C. H(3;2;-1) D. H(0;2;0)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, hình chiếu vuông góc của A(3;2;-1) trên mặt phẳng (Oxy) là điểm
A. H(3;2;0)
B. H(0;0;-1)
C. H(3;2;-1)
D. H(0;2;0)
Đáp án A
Hình chiếu vuông góc của điểm M(x;y;z) trên mặt phẳng (Oxy) là M'(x;y;0)
Cách giải: Hình chiếu vuông góc của A(3;2;-1) trên mặt phẳng (Oxy) là điểm H(3;2;0)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là: A. H(0;-1;0) B. H(0;-1;4) C. H(2;-1;0) D. H(2;0;4).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:
A. H(0;-1;0)
B. H(0;-1;4)
C. H(2;-1;0)
D. H(2;0;4).
Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng đi qua điểm M(1;1;1) và vuông góc với hai mặt phẳng (Oxy),(Ozx).
A. y-1=0.
B. x-1=0.
C. z-1=0.
D. x+z-2=0.
trong mặt phẳng hệ tọa độ vuông góc Oxy cho điểm M (-1;1). Viết phương trình đường thẳng đi qua M và tạo với hai trục tọa độ một tam giác vuông cân
) Trong mặt phẳng với hệ tọa độ Oxy Cho điểm A(1;-2) và B(3;4)
1/ Viết phương trình tổng quát của đường thẳng ![]() qua A(2;4) và vuông góc với AB
qua A(2;4) và vuông góc với AB
\(\overrightarrow{AB}=\left(2,6\right)\)
\(\Rightarrow\overrightarrow{n}=\left(-6,2\right)\)
Đường thằng đi qua A(2,4) , nhận vecto \(\overrightarrow{n}\) làm vecto chỉ phương có PT :
\(\left(-6\right)\cdot\left(x-2\right)+2\cdot\left(y-4\right)=0\)
\(\Rightarrow-6x+2y+4=0\)
Đúng 0
Bình luận (0)