Với x, y là hai số dương, dễ dàng chứng minh x + y  2,

do x + y = 2  => 0 < xy ≤ 1 (1)

Ta lại có: 2xy( x2 + y2) ≤ 

=> 0 < 2xy(x2 + y2)  ≤ (x+y)4/4 = 4

=> 0 < xy( x2 + y2) ≤ 2 (2)

Nhân (1) với (2) theo vế ta có: x2y2 ( x2 + y2) ≤ 2 (đpcm)

Dấu “=” xảy ra khi x = y = 1

Đáp án D

Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0   (*)

Đặt x + y = u x y = v  ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0  gải ra ta được  u = v + 2 + v 2 + 28 v + 4 4

Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18  , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18  ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0  với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 )  trong đó t 0 = m i n t = m i n ( x y + y x )  với x,y thỏa mãn điều kiện (*).

Ta có :

t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2

Vậy  m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4

Đề lỗi công thức rồi. Bạn xem lại.

Lời giải:
$x^2+2y^2+x^2y^2-10xy+16=0$

$\Leftrightarrow (x^2+y^2-2xy)+(x^2y^2-8xy+16)+y^2=0$

$\Leftrightarrow (x-y)^2+(xy-4)^2+y^2=0$

Vì $(x-y)^2\geq 0; (xy-4)^2\geq 0; y^2\geq 0$ với mọi $x,y$

$\Rightarrow$ để tổng của chúng bằng $0$ thì:

$(x-y)^2=(xy-4)^2=y^2=0$

$\Leftrightarrow x=y=0$ và $xy=4$ (vô lý)

Vậy không tồn tại $x,y$ thỏa mãn đề nên cũng không tồn tại $T$.

Lời giải:Vì $x^2+y^2+z^2=2$ nên:

$P=\frac{x^2+y^2+z^2}{x^2+y^2}+\frac{x^2+y^2+z^2}{y^2+z^2}+\frac{x^2+y^2+z^2}{z^2+x^2}-\frac{x^3+y^3+z^3}{2xyz}$

$=3+\frac{x^2}{y^2+z^2}+\frac{y^2}{x^2+z^2}+\frac{z^2}{x^2+y^2}-\frac{x^3+y^3+z^3}{2xyz}$

$\leq 3+\frac{x^2}{2yz}+\frac{y^2}{2xz}+\frac{z^2}{2xy}-\frac{x^3+y^3+z^3}{2xyz}$

(theo BĐT AM-GM)

$=3+\frac{x^3+y^3+z^3}{2xyz}-\frac{x^3+y^3+z^3}{2xyz}=3$

Vậy $P_{\max}=3$

Dấu "=" xảy ra khi $x=y=z=\sqrt{\frac{2}{3}}$

Đáp án D

Phương pháp giải:

Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến

Lời giải:

Từ giả thiết chia cả 2 vế cho x²y² ta được :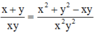  

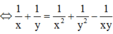
Đặt 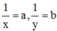 ta có 

Khi đó  

Ta có  mà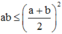 

nên 

Dấu đẳng thức xảy ra khi 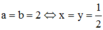. Vậy M_max = 16