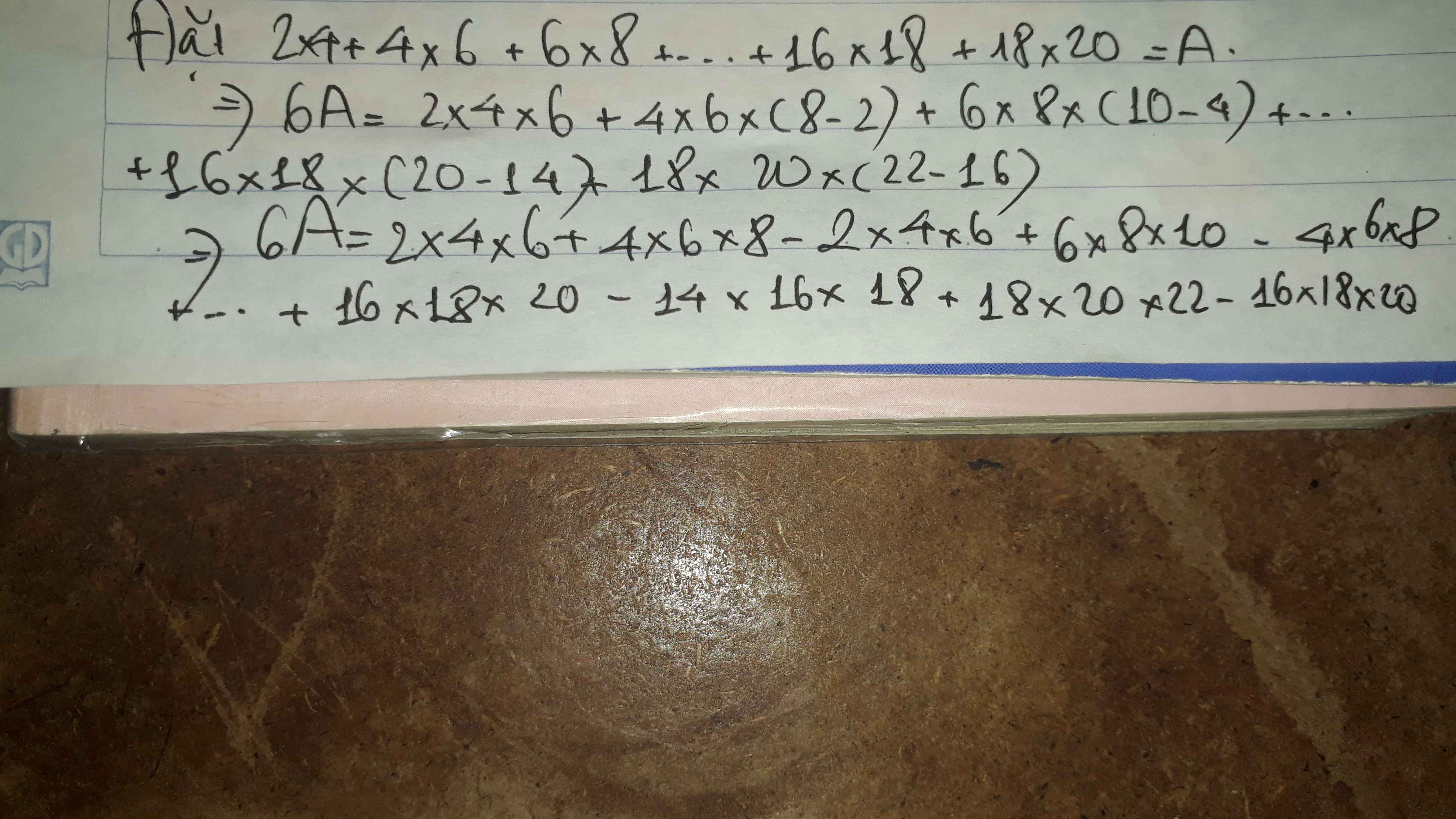\(\frac{4}{2x4}x\frac{4}{4x6}x\frac{4}{6x8}x.......x\frac{4}{16x18}x\frac{4}{18x20}\)

Những câu hỏi liên quan
\(\frac{4}{2x4}+\frac{4}{4x6}+\frac{4}{6x8}+\frac{4}{8x10}+...+\frac{4}{16x18}+\frac{4}{18x20.}\)
Ta gọi biểu thức đó là A
Ta có công thức \(\frac{a}{b.c}=\frac{a}{c-b}.\left(\frac{1}{b}-\frac{1}{c}\right)\)
Dựa vào công thức ta có
\(\frac{4}{2.4}=2.\left(\frac{1}{2}-\frac{1}{4}\right)\)
\(\frac{4}{4.6}=2.\left(\frac{1}{4}-\frac{1}{6}\right)\)
\(....................\)
\(\frac{4}{18.20}=2.\left(\frac{1}{18}-\frac{1}{20}\right)\)
\(\Rightarrow\)\(A=2.\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+....+\frac{1}{18}-\frac{1}{20}\right)\)
\(\Rightarrow\)\(A=2.\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(\Rightarrow\)\(A=2.\left(\frac{9}{20}\right)=\frac{18}{20}\)
Ai thấy đúng thì ủng hộ nha !!!
Đúng 0
Bình luận (0)
sai rồi kết quả phải bằng 9/10 chứ
Đúng 0
Bình luận (0)
\(\frac{4}{2\cdot4}+\frac{4}{4\cdot6}+\frac{4}{6\cdot8}+...+\frac{4}{18\cdot20}\)
\(=2\left(\frac{2}{2\cdot4}+\frac{2}{4\cdot6}+\frac{2}{6\cdot8}+...+\frac{2}{18\cdot20}\right)\)
\(=2\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{18}-\frac{1}{20}\right)\)
\(=2\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(=2\left(\frac{9}{20}\right)\)\(=\frac{18}{20}=\frac{9}{10}\)
Đúng 0
Bình luận (0)
Tính nhanh :
a) 17 x 8 + 51 x 4
b) 2 x 2 x 3 x 5 x 19
c) 54 x 275 + 825 x 15 + 275
d) 100 - 99 + 98 - 97 + 96 - 95 + 94 - 93 + ... + 4 - 3 + 2
e) frac{167x198+98}{198x168-100}
g) frac{1}{1x2}+frac{1}{2x3}+frac{1}{3x4}+...+frac{1}{2019x2020}
h)frac{4}{2x4}+frac{4}{4x6}+frac{4}{6x8}+...+frac{4}{16x18}
k) 1,5 + 2,5 + 3,5 + 4,5 + 5,5 + 6,5 + 7,5 + 8,5
m) frac{1}{2}+frac{1}{6}+frac{1}{12}+frac{1}{20}+...+frac{1}{90}
n) frac{13}{50}+9%+frac{14}{100}+24%
Đọc tiếp
Tính nhanh :
a) 17 x 8 + 51 x 4
b) 2 x 2 x 3 x 5 x 19
c) 54 x 275 + 825 x 15 + 275
d) 100 - 99 + 98 - 97 + 96 - 95 + 94 - 93 + ... + 4 - 3 + 2
e) \(\frac{167x198+98}{198x168-100}\)
g) \(\frac{1}{1x2}+\frac{1}{2x3}+\frac{1}{3x4}+...+\frac{1}{2019x2020}\)
h)\(\frac{4}{2x4}+\frac{4}{4x6}+\frac{4}{6x8}+...+\frac{4}{16x18}\)
k) 1,5 + 2,5 + 3,5 + 4,5 + 5,5 + 6,5 + 7,5 + 8,5
m) \(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{90}\)
n) \(\frac{13}{50}+9\%+\frac{14}{100}+24\%\)
\(17.8+51.4=34.4+51.4=4\left(51+34\right)=4.84=336\) \(2.2.3.5.19=\left(2.5\right).\left(3.19\right).2=10.2.57=570.2=1140\) \(54.275+825.15+275=54.275+45.275+275=275\left(54+45+1\right)=100.275=27500\) \(\frac{167.198+98}{198.168-100}=\frac{167.198+98}{198.167+198-100}=\frac{167.198+98}{167.198+98}=1\)
\(\frac{1}{n}-\frac{1}{n+k}=\frac{k}{n\left(n+k\right)}\Rightarrow\frac{1}{1.2}+\frac{1}{2.3}+.....+\frac{1}{2019.2020}=1-\frac{1}{2}+\frac{1}{2}-....-\frac{1}{2020}=1-\frac{1}{2020}=\frac{2019}{2020}\)
Đúng 0
Bình luận (1)
a) 17 x 8 + 51 x 4
= 17 x 4 x 2 + 17 x 3 x 4
= 17 x 4 x ( 2 + 3 )
= 14 x 4 x 5
= 14 x 20
= 280
b) 2 x 2 x 3 x 5 x 19
= ( 2 x 5 ) x ( 3 x 19 ) x 2
= 10 x 57 x 2
= 570 x 2
= 1140
c) 54 x 275 + 825 x 15 + 275
= 54 x 275 + 275 x 3 x 15 + 275 x 1
= 54 x 275 + 275 x 45 + 275 x 1
= 275 x ( 54 + 45 + 1 )
= 275 x 100
= 27500
d) 100 - 99 + 98 - 97 + 96 - 95 + 94 - 93 + ... + 4 - 3 + 2
= (100 - 99) + (98 - 97) + (96 - 95) + (94 - 93) + ... + (4 - 3) + 2
= (1 + 1 + ... + 1) + 2
( 49 số 1 )
= 49 + 2
= 51
k) 1,5 + 2,5 + 3,5 + 4,5 + 5,5 + 6,5 + 7,5 + 8,5
= ( 1,5 + 8,5 ) + ( 2,5 + 7,5 ) + ( 3,5 + 6,5 ) + ( 4,5 + 5,5 )
= 10 + 10 + 10 + 10
= 40
Đúng 0
Bình luận (1)
m) Đề bn xem ở trên
= \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\)
= \(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{9}-\frac{1}{10}\)
\(=\frac{1}{1}-\frac{1}{10}\)
\(=\frac{10}{10}-\frac{1}{10}=\frac{9}{10}\)
Đúng 0
Bình luận (3)
Xem thêm câu trả lời
tính : a, 4/2x4+4/4x6+4/6x8+......+4/16x18+4/18x20
b, 1/2+1/6+1/12+1/20+......+1/90
\(a,\frac{4}{2.4}+\frac{4}{4.6}+\frac{4}{6.8}+....+\frac{4}{16.18}+\frac{4}{18.20}\)
\(=\frac{4}{2}\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{18}-\frac{1}{20}\right)\)
\(=2\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(=2.\frac{9}{20}\)
\(=\frac{9}{10}\)
\(b,\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{90}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{9.10}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{9}-\frac{1}{10}\)
\(=1-\frac{1}{10}\)
\(=\frac{9}{10}\)
Đúng 0
Bình luận (0)
a, \(\frac{4}{2.4}+\frac{4}{4.6}+\frac{4}{6.8}+..+\frac{4}{16.18}+\frac{4}{18.20}\)
\(=\frac{4}{2}\cdot\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+....+\frac{1}{16}-\frac{1}{18}+\frac{1}{18}-\frac{1}{20}\right)\)
\(=2\cdot\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(=2\cdot\frac{9}{20}=\frac{9}{10}\)
b, \(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{90}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{9.10}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{9}-\frac{1}{10}\)
\(=1-\frac{1}{10}=\frac{9}{10}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
kết quả của phép tính sau là:
4/2x4+4/4x6+4/6x8+4/8x10+...+4/16x18+4/18x20
giải đầy đủ mk tick cho 3 cái luôn
\(\frac{4}{2x4}+\frac{4}{4x6}+\frac{4}{4x8}+...+\frac{4}{16x18}\)
Ai trả lời đúng mik sẽ theo dõi
\(\frac{4}{2\cdot4}+\frac{4}{4\cdot6}+...+\frac{4}{16\cdot18}\)
\(=2\cdot\left(\frac{2}{2\cdot4}+\frac{2}{4\cdot6}+...+\frac{2}{16\cdot18}\right)\)
\(=2\cdot\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+...+\frac{1}{16}-\frac{1}{18}\right)\)
\(=2\cdot\left(\frac{1}{2}-\frac{1}{18}\right)\)
\(=2\cdot\frac{4}{9}\)
\(=\frac{8}{9}\)
Đúng 0
Bình luận (9)
Tìm giá trị của 2x4 + 4x6 + 6x8 +...+16x18+18x20.
\(\frac{1}{2x4}+\frac{1}{4x6}+\frac{1}{6x8}+......+\frac{1}{96x98}+\frac{1}{98x100}.\)
Chú giải: x là dấu nhân
Giải thích mình sẽ **** !!!!!
Đặt A=\(\frac{1}{2x4}+\frac{1}{4x6}+.........+\frac{1}{98x100}\)
2A=\(\frac{2}{2x4}+\frac{2}{4x6}+.............+\frac{2}{98x100}\)
2A=\(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+..........+\frac{1}{98}-\frac{1}{100}\)
2A=\(\frac{1}{2}-\frac{1}{100}\)
2A=\(\frac{49}{100}\)
A=\(\frac{49}{100}:2\)
A=\(\frac{49}{200}\)
Đúng 0
Bình luận (0)
câu này mk gặp rùi nhưng ko biết cách làm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 6: Tính: frac{2}{2x4}+frac{2}{4x6}+frac{2}{6x8}+...+frac{2}{80x82}+frac{2}{82x84}Bài 7: Chuyển phân số thành hỗn số:a) frac{19}{4}b) frac{27}{5}c) frac{56}{8}Bài 8: Tìm số tự nhiên x, biết:a) frac{5}{8}frac{40}{x}b)frac{12}{18}frac{9}{x};frac{15}{20}frac{10}{x}c) 1 frac{5}{4} frac{6}{x}d) frac{3}{5} frac{4}{x} 1Bài 9: Tính: a) 2frac{4}{7}+8frac{3}{9}+5frac{15}{19}b) frac{5}{8}+frac{6}{9}+33frac{5}{9}Bài 10: Ba người thợ chia nhau tiền công. Người thứ nhất được frac{1}{6}tổng số tiền. Người t...
Đọc tiếp
Bài 6: Tính: \(\frac{2}{2x4}+\frac{2}{4x6}+\frac{2}{6x8}+...+\frac{2}{80x82}+\frac{2}{82x84}\)
Bài 7: Chuyển phân số thành hỗn số:
a) \(\frac{19}{4}\)b) \(\frac{27}{5}\)c) \(\frac{56}{8}\)
Bài 8: Tìm số tự nhiên x, biết:
a) \(\frac{5}{8}=\frac{40}{x}\)b)\(\frac{12}{18}=\frac{9}{x};\frac{15}{20}=\frac{10}{x}\)c) \(1< \frac{5}{4}< \frac{6}{x}\)d) \(\frac{3}{5}< \frac{4}{x}< 1\)
Bài 9: Tính:
a) \(2\frac{4}{7}+8\frac{3}{9}+5\frac{15}{19}\)
b) \(\frac{5}{8}+\frac{6}{9}+33\frac{5}{9}\)
Bài 10: Ba người thợ chia nhau tiền công. Người thứ nhất được \(\frac{1}{6}\)tổng số tiền. Người thứ hai được \(\frac{4}{9}\)tổng số tiền. Người thứ ba được hơn người thứ hai 56.000 đồng. Tính số tiền công của mỗi người.
✅ Bài 6: Tính
\(x - \left(\right. \frac{1}{6} x + \frac{4}{9} x \left.\right) = x - \left(\right. \frac{3}{18} x + \frac{8}{18} x \left.\right) = x - \frac{11}{18} x = \frac{7}{18} x\)
Biểu thức:
\(\frac{2 \times 4}{2} + \frac{4 \times 6}{2} + \frac{6 \times 8}{2} + \hdots + \frac{80 \times 82}{2} + \frac{82 \times 84}{2}\)
Nhận thấy:
\(\frac{a \times \left(\right. a + 2 \left.\right)}{2} = \frac{a \left(\right. a + 2 \left.\right)}{2} = \frac{a^{2} + 2 a}{2}\)
Ta có dãy số:
\(a = 2 , 4 , 6 , . . . , 82\) là cấp số cộng (công sai 2), gồm:
\(\frac{82 - 2}{2} + 1 = 41 \&\text{nbsp};\text{s} \overset{ˊ}{\hat{\text{o}}} \&\text{nbsp};\text{h}ạ\text{ng}\)
Tổng cần tính là:
\(\underset{a = 2 , 4 , . . . , 82}{\sum} \frac{a \left(\right. a + 2 \left.\right)}{2} = \underset{a = 2 , 4 , . . . , 82}{\sum} \frac{a^{2} + 2 a}{2} = \frac{1}{2} \sum \left(\right. a^{2} + 2 a \left.\right)\)
Tính bằng máy hoặc từng bước cụ thể sẽ cho:
\(\boxed{57820}\)
✅ Bài 7: Chuyển phân số thành hỗn sốa) \(\frac{19}{4} = 4 \frac{3}{4}\)
b) \(\frac{27}{5} = 5 \frac{2}{5}\)
c) \(\frac{56}{8} = 7\)
\(\frac{5}{8} = \frac{x}{40} \Rightarrow x = \frac{5 \times 40}{8} = 25\)
b)\(\frac{12}{18} = \frac{2}{3} = \frac{x}{9} \Rightarrow x = 2 \times 3 = 6 \Rightarrow \frac{15}{20} = \frac{3}{4} = \frac{x}{10} \Rightarrow x = 3 \times 2.5 = 7.5 \Rightarrow \text{Kh} \hat{\text{o}} \text{ng}\&\text{nbsp};\text{th}ỏ\text{a}\&\text{nbsp};\text{m} \overset{\sim}{\text{a}} \text{n}\&\text{nbsp};\text{v} \overset{ˋ}{\imath} \&\text{nbsp};\text{x}\&\text{nbsp};\text{ph}ả\text{i}\&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{s} \overset{ˊ}{\hat{\text{o}}} \&\text{nbsp};\text{t}ự\&\text{nbsp};\text{nhi} \hat{\text{e}} \text{n}\)
→ Cặp tỉ số không bằng nhau
c)Tìm \(x\) sao cho:
\(1 < \frac{4}{5} < \frac{x}{6} \Rightarrow \frac{4}{5} = 0,8 \Rightarrow x > 6 \times 0,8 = 4,8 \Rightarrow x \geq 5 \Rightarrow \boxed{x = 5 , 6 , 7 , \ldots}\)
d)Tìm \(x\) sao cho:
\(\frac{3}{5} < \frac{x}{4} < 1 \Rightarrow \frac{3}{5} = 0,6 \Rightarrow x > 4 \times 0,6 = 2,4 \Rightarrow x \geq 3 \Rightarrow x < 4 \Rightarrow x = 3\)
→ Đáp án: \(\boxed{x = 3}\)
✅ Bài 9: Tính phân sốa)\(2 \frac{4}{7} + 8 \frac{3}{9} + 5 \frac{15}{19} \Rightarrow \frac{18}{7} + \frac{75}{9} + \frac{110}{19} \Rightarrow \text{Quy}\&\text{nbsp};đ \overset{ˋ}{\hat{\text{o}}} \text{ng}\&\text{nbsp};\text{v} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{c}ộ\text{ng}\&\text{nbsp};\text{v} \overset{ˋ}{\text{a}} \text{o}\&\text{nbsp};(\text{ho}ặ\text{c}\&\text{nbsp};\text{d} \overset{ˋ}{\text{u}} \text{ng}\&\text{nbsp};\text{m} \overset{ˊ}{\text{a}} \text{y}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{nh}) \Rightarrow \boxed{\approx 33 , 6}\)
(Tùy yêu cầu đề, nếu cần kết quả phân số chính xác bạn có thể yêu cầu mình làm chi tiết)
✅ Bài 10: Bài toán chia tiền côngGọi tổng số tiền là x đồng
Người 1: \(\frac{1}{6} x\)Người 2: \(\frac{4}{9} x\)Người 3: Số còn lại:\(x - \left(\right. \frac{1}{6} x + \frac{4}{9} x \left.\right) = x - \left(\right. \frac{3}{18} x + \frac{8}{18} x \left.\right) = x - \frac{11}{18} x = \frac{7}{18} x\)
Người 3 hơn người 2 là 56.000 đồng:
\(\frac{7}{18} x - \frac{4}{9} x = 56000 \Rightarrow \frac{7}{18} x - \frac{8}{18} x = - \frac{1}{18} x = 56000 \Rightarrow x = - 56000 \times 18 = - 1.008.000\)
Kết quả âm → kiểm tra lại:
Người 3 hơn người thứ hai:\(\frac{7}{18} x - \frac{4}{9} x = \frac{7}{18} x - \frac{8}{18} x = - \frac{1}{18} x \rightarrow \text{Kh} \hat{\text{o}} \text{ng}\&\text{nbsp};\text{th}ể\&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{h}o\text{n}\)
Sai ở chỗ: người thứ ba hơn người thứ hai → vậy người thứ ba phải được nhiều hơn, nên:
\(\frac{7}{18} x - \frac{4}{9} x = 56000 \Rightarrow \frac{7}{18} x - \frac{8}{18} x = - \frac{1}{18} x = 56000 \Rightarrow \text{V} \overset{\sim}{\hat{\text{a}}} \text{n}\&\text{nbsp}; \hat{\text{a}} \text{m}\)
→ Phép trừ ngược, đúng công thức là:
\(\frac{7}{18} x - \frac{4}{9} x = 56000 \Rightarrow \frac{7}{18} x - \frac{8}{18} x = - \frac{1}{18} x = 56000 \Rightarrow x = - 1.008.000\)
→ Không hợp lý.
➤ Sửa lại phần chia:Người thứ ba được nhiều hơn người thứ hai, nên phải là:
\(\frac{4}{9} x + 56000 = \frac{7}{18} x \Rightarrow \frac{7}{18} x - \frac{4}{9} x = 56000 \Rightarrow \frac{7}{18} x - \frac{8}{18} x = - \frac{1}{18} x = 56000 \Rightarrow x = - 1.008.000\)
Vẫn âm → vẫn sai chiều.
✅ Cách đúng:Người thứ ba hơn người thứ hai ⇒
\(\frac{7}{18} x = \frac{4}{9} x + 56000 \Rightarrow \frac{7}{18} x - \frac{4}{9} x = 56000 \Rightarrow \frac{7}{18} x - \frac{8}{18} x = - \frac{1}{18} x = 56000 \Rightarrow x = - 1.008.000\)
Vẫn ra âm → chứng tỏ giả thiết mâu thuẫn hoặc đề có sai sót.
❗Hãy xác nhận lại:
"Người thứ ba được hơn người thứ hai 56.000 đồng"
→ thì:
\(\frac{7}{18} x - \frac{4}{9} x = 56000 \Rightarrow \frac{7}{18} x - \frac{8}{18} x = - \frac{1}{18} x = 56000 \Rightarrow x = - 1.008.000 \&\text{nbsp};(\text{v} \hat{\text{o}} \&\text{nbsp};\text{l} \overset{ˊ}{\text{y}} )\)
→ Vậy có thể người thứ ba được ÍT hơn người thứ hai 56.000 đồng?
Nếu đề đúng là “người thứ ba được ít hơn người thứ hai 56.000 đồng”, ta có:
\(\frac{4}{9} x - \frac{7}{18} x = 56000 \Rightarrow \frac{8 - 7}{18} x = \frac{1}{18} x = 56000 \Rightarrow x = \boxed{1.008.000}\)
✅ Suy ra số tiền công:
Người 1: \(\frac{1}{6} x = \frac{1.008.000}{6} = \boxed{168.000 \&\text{nbsp};đ \overset{ˋ}{\hat{\text{o}}} \text{ng}}\)Người 2: ( \frac{4}{9}x =
Đúng 0
Bình luận (0)
A=\(\frac{1}{2x4}+\frac{1}{4x6}+\frac{1}{6x8}+......+\frac{1}{98x100}\)
\(A=\frac{1}{2\times4}+\frac{1}{4\times6}+\frac{1}{6\times8}+...+\frac{1}{98\times100}\)
\(=\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{96}-\frac{1}{98}+\frac{1}{98}-\frac{1}{100}\)
\(=\frac{1}{2}-\frac{1}{100}\)
\(=\frac{50}{100}-\frac{1}{100}\)
\(=\frac{49}{100}\)
Vậy: \(A=\frac{49}{100}\)
Đúng 0
Bình luận (0)
Ta có:\(2A=2\left(\frac{1}{2.4}+\frac{1}{4.6}+....+\frac{1}{98.100}\right)\)
\(=\frac{2}{2.4}+\frac{2}{4.6}+....+\frac{2}{98.100}\)
\(=\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+....+\frac{1}{98}-\frac{1}{100}\)
\(=\frac{1}{2}-\frac{1}{100}=\frac{49}{100}\)
\(\Rightarrow A=\frac{49}{100}\div2=\frac{49}{200}\)
Vậy giá trị của A là \(\frac{49}{200}\)
Đúng 0
Bình luận (0)