Tìm m để phương trình sau vô nghiệm
x2 - 2mx +3m +2 = 0
Những câu hỏi liên quan
a Tìm m để phương trình vô nghiệm: x2 - (2m - 3)x + m2 = 0.
b Tìm m để phương trình vô nghiệm: (m - 1)x2 - 2mx + m -2 = 0.
c Tìm m để phương trình vô nghiệm: (2 - m)x2 - 2(m + 1)x + 4 - m = 0
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
Đúng 0
Bình luận (0)
Tìm m để hệ bất phương trình : có nghiệm, vô nghiệma) {x+m−103m−2−x0{x+m−103m−2−x0b) {x−10mx−30{x−10mx−30c) {x+4m2≤2mx+13x+22x−1{x+4m2≤2mx+13x+22x−1d) {7x−2≥−4x+192x−3m+20{7x−2≥−4x+192x−3m+20 e) {mx−10(3m−2)x−m0
Đọc tiếp
Tìm m để hệ bất phương trình : có nghiệm, vô nghiệm
a)
b)
c)
d)
e)
Tìm m để bất phương trình sau vô nghiệm: f(x) = (m - 2) x 2 - 2mx + m + 1 > 0
f(x) = (m-2) x 2 - 2mx + m + 1 > 0 (*)
Với m = 2 thì bất phương trình (*) trở thành:
f(x) = -4x + 3 > 0 ⇔ x < 3/4
Vậy với m = 2 thì bất phương trình (*) có nghiệm x < 3/4 nên m = 2 (loại)
Với m ≠ 2 thì bất phương trình (*) vô nghiệm khi và chỉ khi
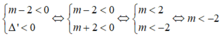
Vậy với m < -2 thì bất phương trình (*) vô nghiệm
Đúng 0
Bình luận (0)
chứng minh phương trình vô nghiệm
x2-5x+20=0
\(x^2-5x+20=0\)
\(\Leftrightarrow x^2-2.x.\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2-\left(\dfrac{5}{2}\right)^2+20=0\)
\(\Leftrightarrow\left(x-\dfrac{5}{2}\right)^2+\dfrac{55}{4}=0\)
\(\Leftrightarrow\left(x-\dfrac{5}{2}\right)^2=-\dfrac{55}{4}\)
Vì \(\left(x-\dfrac{5}{2}\right)^2\ge0\forall x\in R\)
Mà \(\left(x-\dfrac{5}{2}\right)^2=-\dfrac{55}{4}\) (vô lí)
\(\Rightarrow S=\varnothing\)
Đúng 3
Bình luận (0)
Lời giải:
$x^2-5x+20=x^2-2.2,5x+2,5^2+13,75=(x-2,5)^2+13,75\geq 0+13,75>0$ với mọi $x\in\mathbb{R}$
Do đó pt $x^2-5x+20=0$ vô nghiệm (đpcm)
Đúng 1
Bình luận (0)
Tìm m để phương trình (m-1) x 2 - 2mx + 3m - 2 = 0 có hai nghiệm dương phân biệt?
A. m < 0,1 < m < 2
B. 1 < m < 2
C. m > 2
D. m < 1/2
Đáp án: B
(m - 1) x 2 - 2mx + 3m - 2 = 0 (*)
Để phương trình (*) có hai nghiệm dương phân biệt thì:
Đúng 0
Bình luận (0)
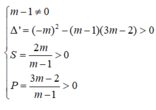
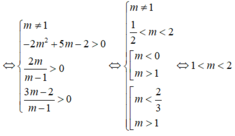
1. Định m để bất phương trình m(x-1) > 2mx - 3 có vô số nghiệm
2. Tìm m để m(x-2) + m -1 < 0 bất phương trình có vô số nghiệm
Gọi n là số các giá trị của tham số m để bất phương trình
2
m
-
4
x
3
+
2
x
2
+
m
2
-
3
m
+...
Đọc tiếp
Gọi n là số các giá trị của tham số m để bất phương trình 2 m - 4 x 3 + 2 x 2 + m 2 - 3 m + 2 x 2 + 2 x - m 3 - m 2 - 2 m x + 2 < 0 vô nghiệm. Giá trị của n bằng:
A. 5
B. 1
C. 4
D. 2
Cho phương trình ( m – 3 ) x 2 – 2 m x + m − 6 = 0 . Tìm các giá trị của m để phương trình vô nghiệm
A. m < −2
B. m < 2
C. m < 3
D. m < −3
Phương trình (m – 3)x2 – 2mx + m − 6 = 0
có a = m – 3; b’ = −m; c = m – 6
Suy ra Δ ' = (−m)2 – (m − 3)(m – 6) = 9m – 18
TH1: m – 3 = 0 ⇔ m = 3 −6x – 3 = 0
⇔ x = − 1 2
TH2: m – 3 ≠ 0 ⇔ m ≠ 3
Để phương trình vô nghiệm thì:
a ≠ 0 Δ ' < 0 ⇔ m ≠ 3 9 m − 18 < 0 ⇔ m ≠ 3 m < 2 ⇔ m < 2
Vậy m < 2 là giá trị cần tìm
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Tìm m để phương trình sau vô nghiệm (2m-1)x+3m-5=0