Cứu em câu naỳy:(

Những câu hỏi liên quan
cứu em câu 3 và tác dụng ở câu 2, em đang cần gấppppp
cứu em câu này!!!!
Cứu em với giải với giải thích ra hộ em với nhoa câu 5 câu 6 ạ
5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
Đúng 5
Bình luận (1)
Cứu em câu 5😭
Câu 6:
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
Đúng 1
Bình luận (0)
Tính AH
SinC= AH/AC= x/12
=>x = AC. Sin30 độ = 12. Sin30 độ =6 cm
=>x= AH =6(cm)
Tính AB
CosA=AH/AB=6/y
=>y= AH:Cos40 độ = 6:Cos40 độ = 7,832 cm
=>y=AB=7,832 cm
Đúng 1
Bình luận (0)
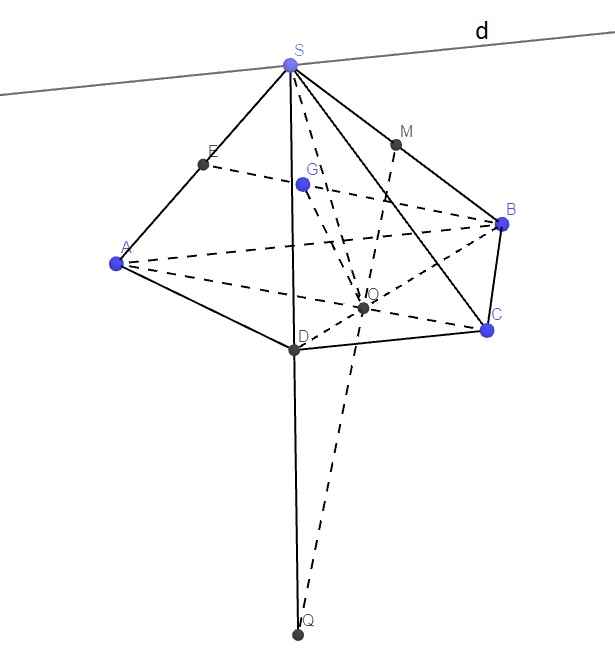
Câu 15 ạ cứu em với:((
a.
Ta có: \(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(S=\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Do \(AB||CD\Rightarrow\) giao tuyến của (SAC) và (SBD) là một đường thẳng song song AB và CD
Qua S kẻ đường thẳng \(d||AB\)
Do \(S=\left(SAB\right)\cap\left(SCD\right)\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
\(O\in AC\in\left(AMC\right)\Rightarrow OM\in\left(AMC\right)\)
\(\left\{{}\begin{matrix}M\in SB\\O\in BD\end{matrix}\right.\) \(\Rightarrow OM\in\left(SBD\right)\) \(\Rightarrow OM=\left(AMC\right)\cap\left(SBD\right)\)
Trong mp (SBD), kéo dài OM cắt SD tại Q
\(\Rightarrow Q=SD\in\left(AMC\right)\)
c.
Gọi E là trung điểm SA
Do G là trọng tâm tam giác SAB \(\Rightarrow G\in BE\) và \(BG=\dfrac{2}{3}BE\Rightarrow\dfrac{BG}{BE}=\dfrac{2}{3}\) (1)
Do \(AB||CD\) , áp dụng định lý Talet: \(\dfrac{OD}{OB}=\dfrac{CD}{AB}=\dfrac{1}{2}\Rightarrow\dfrac{OD}{OB}+1=\dfrac{3}{2}\Rightarrow\dfrac{OD+OB}{OB}=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{BD}{OB}=\dfrac{3}{2}\Rightarrow\dfrac{BO}{BD}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow\dfrac{BG}{BE}=\dfrac{BO}{BD}\Rightarrow OG||ED\) (Talet đảo)
Mà \(ED\in\left(SAD\right)\Rightarrow OG||\left(SAD\right)\)
Đúng 0
Bình luận (0)
cứu em câu này với ạ 
 câu b ai cứu em với
câu b ai cứu em với
`b,`
`@` \(\text{Na}_2\text{O}\)
`-` Gồm `2` nguyên tử `Na`, `1` nguyên tử `O`
`@`\(\text{H}_2\text{SO}_4\)
`-` Gồm `2` nguyên tử `H`, `1` nguyên tử `S,` `4` nguyên tử `O`
`@`\(\text{Ca}_3\left(\text{PO}_4\right)_2\)
`-` Gồm `3` nguyên tử `Ca`, `2` nguyên tử `P`, `8` nguyên tử `O`
`@`\(\text{Fe}\left(\text{OH}\right)_3\)
`-` Gồm `1` nguyên tử `Fe`, `3` nguyên `O`, `3` nguyên tử `H`
`@`\(\text{ P}_2\text{O}_5\)
`-` Gồm `2` nguyên tử `P`, `5` nguyên tử `O`.
Đúng 0
Bình luận (1)
 câu 1 làm từ câu i cũng được ạ
câu 1 làm từ câu i cũng được ạ
xin mng cứu em D:
1:
i: \(=\dfrac{15}{34}+\dfrac{19}{34}+\dfrac{7}{21}+\dfrac{2}{3}-1-\dfrac{15}{37}\)
\(=1+\dfrac{1}{3}+\dfrac{2}{3}-1-\dfrac{15}{37}\)
\(=1-\dfrac{15}{37}=\dfrac{22}{37}\)
j: \(=1-\left(-27\right)+\dfrac{1}{2}:\dfrac{-1}{8}\)
\(=1+27-4=24\)
k: \(=-8+\dfrac{1}{2}\cdot\dfrac{-4}{1}-15\)
\(=-8-2-15=-25\)
l: \(=3:\dfrac{9}{4}+\dfrac{1}{9}\cdot6\)
\(=3\cdot\dfrac{4}{9}+\dfrac{1}{9}\cdot6\)
\(=\dfrac{4}{3}+\dfrac{2}{3}=2\)
m: \(=9\cdot\dfrac{1}{3}-\left(-27\right)=3+27=30\)
n: \(\sqrt{\dfrac{16}{25}}\cdot\sqrt{\dfrac{121}{64}}-1\dfrac{3}{10}\)
\(=\dfrac{4}{5}\cdot\dfrac{11}{8}-\dfrac{13}{10}\)
\(=\dfrac{11}{10}-\dfrac{13}{10}=-\dfrac{2}{10}=-\dfrac{1}{5}\)
o: \(=\dfrac{9}{8}\cdot12-\dfrac{1}{2}\)
\(=\dfrac{27}{2}-\dfrac{1}{2}=\dfrac{26}{2}=13\)
p: \(=\dfrac{3^2\cdot2^2+3^2\cdot3\cdot2^2+3^2}{-13}\)
\(=\dfrac{3^2\left(2^2+3\cdot2^2+3^2\right)}{-13}\)
\(=\dfrac{9\cdot\left(4+3\cdot4+9\right)}{-13}\)
\(=\dfrac{9\cdot25}{-13}=-\dfrac{225}{13}\)
Đúng 4
Bình luận (0)
 cứu em 2 câu này vs ạ
cứu em 2 câu này vs ạ
Câu 2:
a: *Vẽ đồ thị
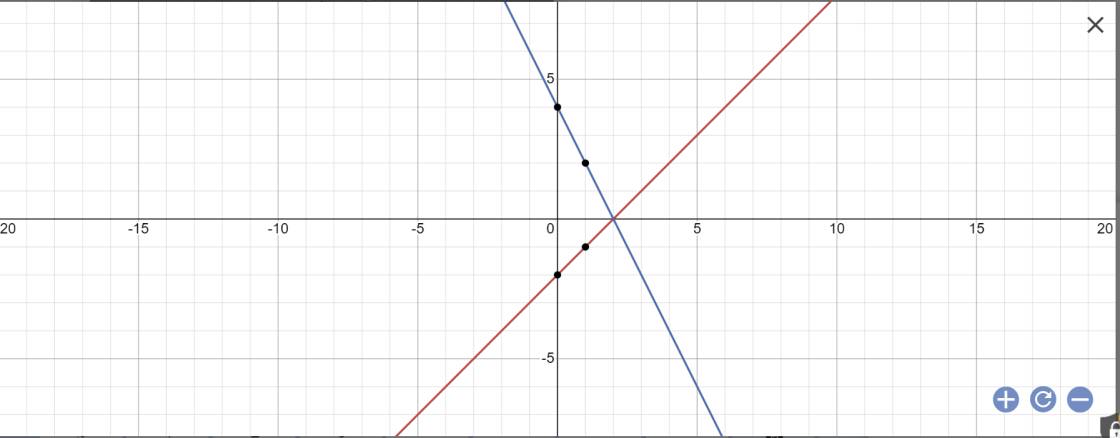
*Tìm giao điểm:
Phương trình hoành độ giao điểm là:
x-2=-2x+4
=>x+2x=4+2
=>3x=6
=>x=2
Thay x=2 vào y=x-2, ta được:
y=2-2=0
Vậy: (d1):y=x-2 cắt (d2): y=-2x+4 tại A(2;0)
b: *Vẽ đồ thị
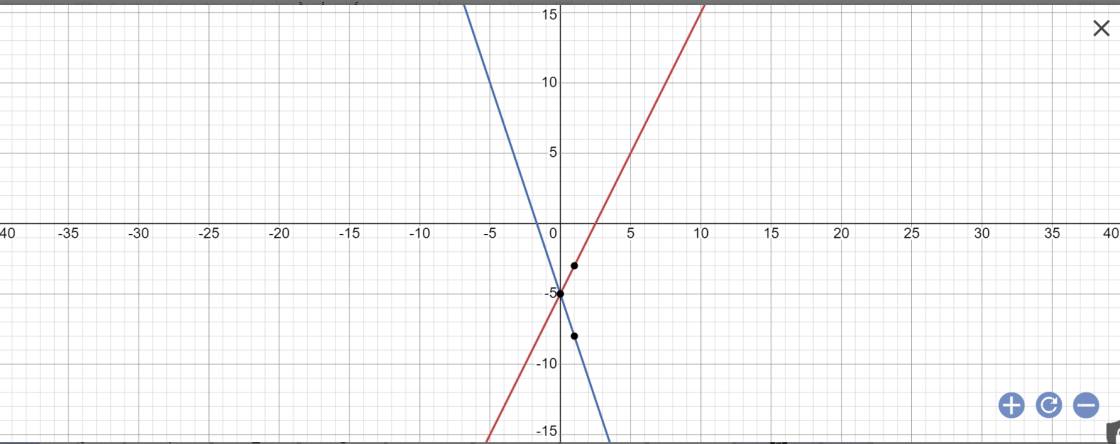
*Tìm giao điểm
Phương trình hoành độ giao điểm là:
2x-5=-3x-5
=>2x+3x=-5+5=0
=>5x=0
=>x=0
Thay x=0 vào y=2x-5, ta được:
\(y=2\cdot0-5=-5\)
Vậy: (d1): y=2x-5 cắt (d2):y=-3x-5 tại A(0;-5)
c: *Vẽ đồ thị
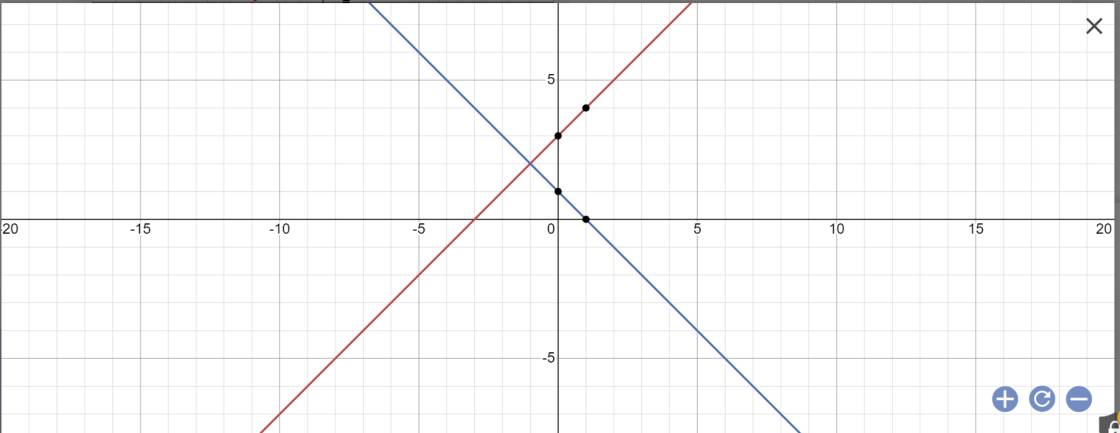
*Tìm giao điểm
Phương trình hoành độ giao điểm là:
x+3=-x+1
=>x+x=1-3
=>2x=-2
=>x=-1
Thay x=-1 vào y=x+3, ta được:
y=-1+3=2
vậy: (d1): y=x+3 và (d2): y=-x+1 cắt nhau tại C(-1;2)
Đúng 2
Bình luận (0)