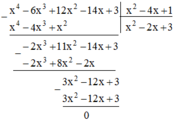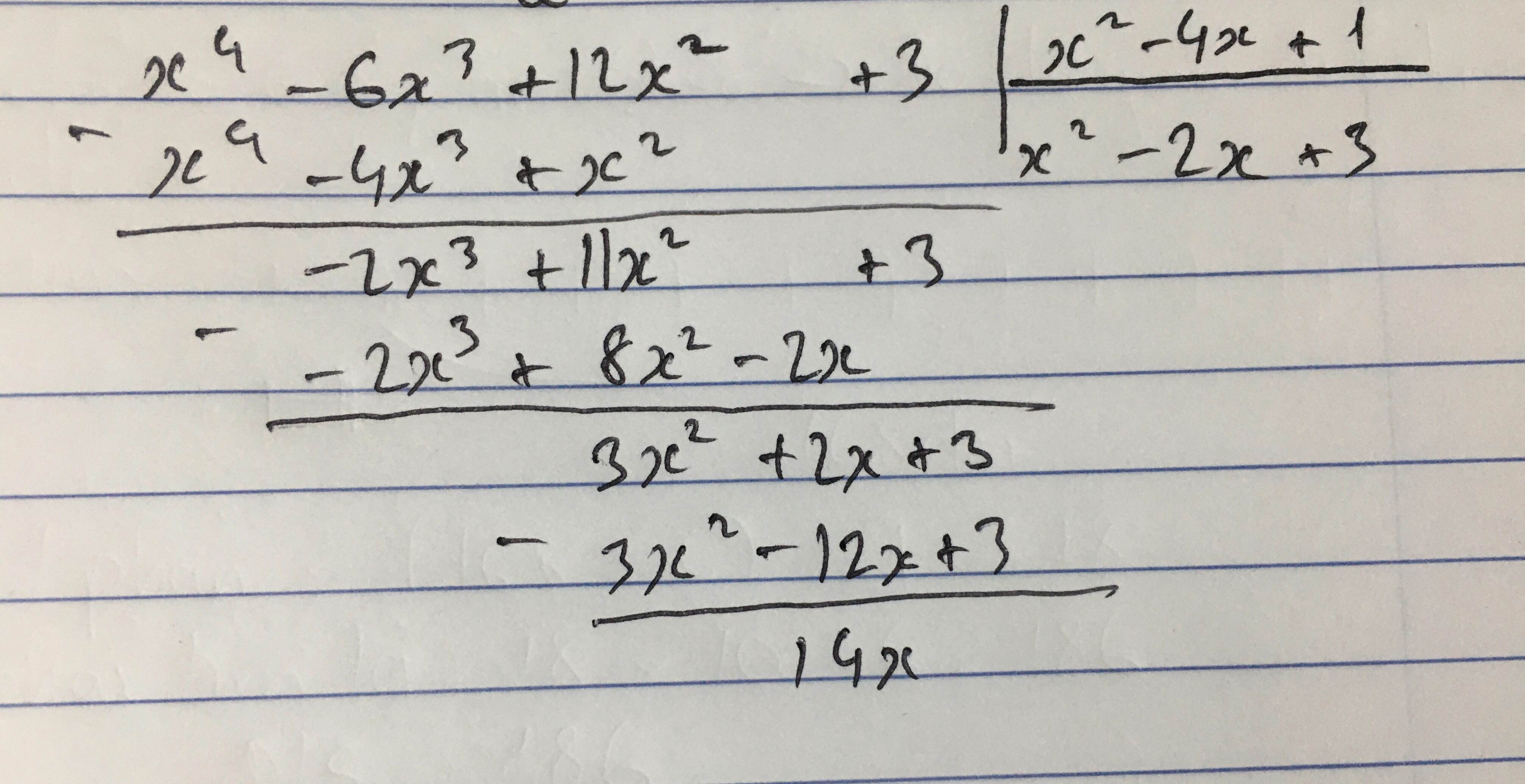Phân tích đa thức thành nhân tử
A= x4 - 6x3+12x2 -14x-3

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử:a)
x
4
-
6
x
3
+
12
x
2
- 14x + 3.b)
x
4
+
6
x
3
+
7
x
2
-6x +...
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) x 4 - 6 x 3 + 12 x 2 - 14x + 3.
b) x 4 + 6 x 3 + 7 x 2 -6x + l.
a) ( x 2 – 4x + 1)( x 2 – 2x + 3).
b) ( x 2 + 5x – 1)( x 2 + x – 1).
Đúng 0
Bình luận (0)
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
12
x
2
-
14
x
+
3
-
6
x
3
+
x
4
:
1...
Đọc tiếp
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia: 12 x 2 - 14 x + 3 - 6 x 3 + x 4 : 1 - 4 x + x 2
phân tích đa thức sau thành nhân tử
a) x4-27x
b) 27x5+x2
\(x^4-27x=x\left(x^3-27\right)=x\left(x-3\right)\left(x^2+3x+9\right)\)
\(27x^5+x^2=x^2\left(27x^3+1\right)=x^2\left[\left(3x\right)^3+1^3\right]=x^2\left(3x+1\right)\left(9x^2-3x+1\right)\)
Đúng 3
Bình luận (0)
a) x4-27x=x(x3-27)=x(x-3)(x2-3x+9)
b) 27x5+x2=x2(27x3+1)=x2(3x+1)(9x2-3x+1)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử
a) a4 + a2 +1
b)a4+a2 -2
c) x3-5x2-14x
\(a,a^4+a^2+1\)
\(=\left(a^2\right)^2+2a^2+1-a^2\)
\(=\left(a^2+1\right)^2-a^2\)
\(=\left(a^2+1-a\right)\left(a^2+1+a\right)\)
\(---\)
\(b,a^4+a^2-2\)
\(=a^4-a^2+2a^2-2\)
\(=a^2\left(a^2-1\right)+2\left(a^2-1\right)\)
\(=\left(a^2-1\right)\left(a^2+2\right)\)
\(=\left(a-1\right)\left(a+1\right)\left(a^2+2\right)\)
\(---\)
\(c,x^3-5x^2-14x\)
\(=x^3+2x^2-7x^2-14x\)
\(=x^2\left(x+2\right)-7x\left(x+2\right)\)
\(=\left(x+2\right)\left(x^2-7x\right)\)
\(=x\left(x+2\right)\left(x-7\right)\)
Đúng 2
Bình luận (0)
\(a.a^4+a^2+1\)
\(=\left(a^4+2a^2+1\right)-a^2\)
\(=\left(a^2+1\right)^2-a^2\)
\(=\left(a^2+1+a\right)\left(a^2+1-a\right)\)
\(b.a^4+a^2-2\)
\(=a^4+2a^2-a^2-2\)
\(=a^2\left(a^2+2\right)-\left(a^2-2\right)\)
\(=\left(a^2+2\right)\left(a^2-1\right)\)
\(=\left(a^2+2\right)\left(a-1\right)\left(a+1\right)\)
\(c.x^3-5x^2-14x\)
\(=x^3+2x^2-7x^2-14\)
\(=x^3\left(x+2\right)-7x\left(x+2\right)\)
\(=\left(x^3-7x\right)\left(x+2\right)\)
\(=x\left(x-7x\right)\left(x+2\right)\)
Đúng 0
Bình luận (0)
phân tích da thức sau thành nhân tử
a) x4+x3+x+1
b)x4-x3-x2+1
c)x2y+xy2-x-y
d) ax2+a2y-7x-7y
e) ax2+ay-bx2-by
g) 12x2-3xy+8xz-2yz
h) x3-x2y-x2z-xyz
mợi người giúp em nha
Câu 2: Phân tích các đa thức sau thành nhân tử:
a) 3x. (x – 2 ) – 4x + 8 b) – 6xy2 + 6x3 + 12x2 + 6x
c) 2x2 + 4x – 30
bài 1 : phân tích đa thức thành nhân tử
a/ 2x2 (x – 1) + 4x (1 – x) b/ x4 – 27x c/ x2 – 4x + 3 d / x4 + x2 + 1
b: \(=x\left(x-3\right)\left(x^2+3x+9\right)\)
Đúng 0
Bình luận (0)
a/ 2x^2 (x – 1) + 4x (1 – x)
= 2x^2(x – 1) – 4x (x – 1)
= (x – 1)( 2x^2 – 4x)
=2x(x – 1)(x – 2)
Đúng 0
Bình luận (0)
Chia đa thức cho đa thức:
(12x2+3-6x3+x4) : (1-4x+x2)
\(\dfrac{x^4-6x^3+12x^2+3}{x^2-4x+1}\)
\(=\dfrac{x^4-4x^3+x^2-2x^3+8x^2-2x+2x^2-8x+2+10x+1}{x^2-4x+1}\)
\(=x^2-2x+2+\dfrac{10x+1}{x^2-4x+1}\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
a)x4 - x3y + x - y
b)a2 - 2a + 1 - 9b2
a: =x^3(x-y)+(x-y)
=(x-y)(x^3+1)
=(x-y)(x+1)(x^2-x+1)
b: =(a-1)^2-9b^2
=(a-1-3b)(a-1+3b)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
a) x4+\(\dfrac{1}{4}\)y8
b) \(\dfrac{1}{4}\)x4+y8
c) 64x4+y4
d) x4+\(\dfrac{1}{64}\)y4
Lời giải:
a.
$=(x^2)^2+(\frac{1}{2}y^4)^2+2.x^2.\frac{1}{2}y^4-x^2y^4$
$=(x^2+\frac{1}{2}y^4)^2-(xy^2)^2$
$=(x^2+\frac{1}{2}y^4-xy^2)(x^2+\frac{1}{2}y^4+xy^2)$
b.
$=(\frac{1}{2}x^2)^2+(y^4)^2+2.\frac{1}{2}x^2.y^4-x^2y^4$
$=(\frac{1}{2}x^2+y^4)^2-(xy^2)^2$
$=(\frac{1}{2}x^2+y^4-xy^2)(\frac{1}{2}x^2+y^4+xy^2)$
c.
$=(8x^2)^2+(y^2)^2+2.8x^2.y^2-16x^2y^2$
$=(8x^2+y^2)^2-(4xy)^2=(8x^2+y^2-4xy)(8x^2+y^2+4xy)$
d.
$=\frac{64x^4+y^4}{64}=\frac{1}{64}(8x^2+y^2-4xy)(8x^2+y^2+4xy)$
Đúng 1
Bình luận (0)
c: \(64x^4+y^4\)
\(=64x^4+16x^2y^2+y^4-16x^2y^2\)
\(=\left(8x^2+y^2\right)^2-\left(4xy\right)^2\)
\(=\left(8x^2+y^2-4xy\right)\left(8x^2+y^2+4xy\right)\)
Đúng 0
Bình luận (0)