Cho ba đường thẳng a,b và c phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?

Những câu hỏi liên quan
Cho 3 đường thẳng a, b, c phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?
A. Ba đường thẳng đôi một cắt nhau.
B. a cắt b và a song song c.
C. Ba đường thẳng đôi một song song.
D. a song song b và a cắt c.
Đáp án là C
Ba đường thẳng đôi một không có giao điểm nghĩa là:
• a, b không có giao điểm hay a song song b.
• b, c không có giao điểm hay b song song c.
• a, c không có giao điểm hay a song song c.
Vậy ba đường thẳng đôi một song song.
Đúng 0
Bình luận (0)
Cho 3 đường thẳng a, b, c phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm? A. Ba đường thẳng đôi một cắt nhau. B. a cắt b và a song song c. C. Ba đường thẳng đôi một song song. D. a song song b và a cắt c.
Đọc tiếp
Cho 3 đường thẳng a, b, c phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?
A. Ba đường thẳng đôi một cắt nhau.
B. a cắt b và a song song c.
C. Ba đường thẳng đôi một song song.
D. a song song b và a cắt c.
Đáp án là C
Ba đường thẳng đôi một không có giao điểm nghĩa là:
• a, b không có giao điểm hay a song song b.
• b, c không có giao điểm hay b song song c.
• a, c không có giao điểm hay a song song c.
Vậy ba đường thẳng đôi một song song.
Đúng 0
Bình luận (0)
Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a(P)∩(R),b(Q)∩(R),c(P)∩(Q)- Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c có đi qua điểm M hay không (Hình 38a)?- Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a có song song với đường thẳng c hay không (Hình 38b)?
Đọc tiếp
Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a=(P)∩(R),b=(Q)∩(R),c=(P)∩(Q)
- Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c có đi qua điểm M hay không (Hình 38a)?
- Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a có song song với đường thẳng c hay không (Hình 38b)?
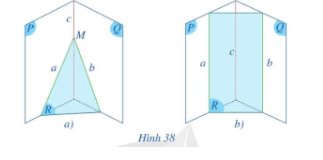
– Ta có: a ∩ b = {M}
Mà a ⊂ (P); b ⊂ (Q)
Nên M ∈ (P) và M ∈ (Q)
Do đó M là giao điểm của (P) và (Q).
Mà (P) ∩ (Q) = c, suy ra M ∈ c.
Vậy đường thằng c đi qua điểm M.
– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.
Khi đó N ∈ a mà a ⊂ (R) nên N ∈ (R)
N ∈ c mà c ⊂ (Q) nên N ∈ (Q)
Do đó N là giao điểm của (R) và (Q).
Mà (Q) ∩ (R) = b
Đúng 0
Bình luận (0)
A. Cho n điểm phân biệt trong đó không có 3điểm nào thẳng hàng. Qua 2 điểm ta vẽ được một đường thẳng. Tìm n
B. Cho n điểm phân biệt trong đó có 7điểm thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm có tất cả 190 đường thẳng. Tím n
C. Cho 20đừong thẳng đôi một cắt nhau và không có ba đường thẳng nào đong quy. Hỏi có bao nhiêu giao điểm tào thành
A. Câu hỏi của Hà Nhật Anh - Toán lớp 6 - Học toán với OnlineMath
Mỗi câu sau đây là đúng hay sai ?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước
c) Có đúng 6 đường thẳng đi qua bốn điểm (phân biệt) cho trước
d) Hai đường thẳng phân biệt thì song song với nhau
e) Hai đường thẳng không cắt nhau thì song song với nhau
f) Hai đường thẳng không song song thì cắt nhau
g) Hai đường thẳng không phân biệt thì trùng nhau
h) Ba đường thẳng phân biệt, từng đôi một cắt nhau thì...
Đọc tiếp
Mỗi câu sau đây là đúng hay sai ?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước
c) Có đúng 6 đường thẳng đi qua bốn điểm (phân biệt) cho trước
d) Hai đường thẳng phân biệt thì song song với nhau
e) Hai đường thẳng không cắt nhau thì song song với nhau
f) Hai đường thẳng không song song thì cắt nhau
g) Hai đường thẳng không phân biệt thì trùng nhau
h) Ba đường thẳng phân biệt, từng đôi một cắt nhau thì có đúng 3 giao điểm (phân biệt)
Mỗi câu sau đây là đúng hay sai ?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước
Đúng
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước
Sai
c) Có đúng 6 đường thẳng đi qua bốn điểm (phân biệt) cho trước
Sai
d) Hai đường thẳng phân biệt thì song song với nhau
Sai
e) Hai đường thẳng không cắt nhau thì song song với nhau
Sai
f) Hai đường thẳng không song song thì cắt nhau
Sai
g) Hai đường thẳng không phân biệt thì trùng nhau
Đúng
h) Ba đường thẳng phân biệt, từng đôi một cắt nhau thì có đúng 3 giao điểm (phân biệt)
Sai
Đúng 0
Bình luận (0)
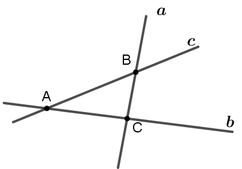
Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. Tìm số giao điểm phân biệt của ba đường thẳng đã cho.
A. 6
B. 2
C. 1
D. 3
Đáp án C
Nếu ba đường thẳng a,b,c đôi một cắt nhau và không đồng phẳng thì chúng chỉ có thể đồng quy tại một điểm.

Đúng 0
Bình luận (0)
Cho biết có thể vẽ được bao nhiêu đường thẳng (phân biệt) trong mỗi trường hợp sau :
a) Với hai điểm (phân biệt) cho trước
b) Với ba điểm (phân biệt) cho trước và không thẳng hàng
c) Với bốn điểm (phân biệt) cho trước, trong đó không có 3 điểm nào thẳng hàng
Cho biết có thể vẽ được bao nhiêu đường thẳng (phân biệt) trong mỗi trường hợp sau :
a) Với hai điểm (phân biệt) cho trước
Vẽ đc 1
b) Với ba điểm (phân biệt) cho trước và không thẳng hàng
Vẽ đc 3
c) Với bốn điểm (phân biệt) cho trước, trong đó không có 3 điểm nào thẳng hàng
Vẽ đc 6
Đúng 0
Bình luận (0)
Cho biết có thể vẽ được bao nhiêu đường thẳng (phân biệt) trong mỗi trường hợp sau:
a, Với hai điểm (phân biệt)cho trước: vẽ được 2
b, Với ba điểm (phân biệt) cho trước và không thẳng hàng: vẽ được 3
c,Với bốn điểm phân biệt cho trước trong đó không có 3 điểm nào thẳng hàng: vẽ được 6
Đúng 0
Bình luận (0)
Cho biết có thể vẽ được bao nhiêu đường thẳng ( phân biệt ) trong mỗi trường hợp sau
a) Với hai điểm ( phân biệt ) cho trước
b) Với ba điểm ( phân biệt ) cho trước và không thẳng hàng.
c) Với bốn điểm ( phân biệt ) cho trước, trong đó không có 3 điểm nào thẳng hàng.
a: 1 đường thẳng
b: 3 đường thẳng
c: 6 đường thẳng
Đúng 0
Bình luận (0)
Cho trước một điểm O. Em hãy: - Vẽ ba đường thẳng phân biệt a, b, c đôi một cắt nhau sao cho chúng chỉ có một giao điểm duy nhất là O;- Vẽ đường thẳng m cắt hai đường thẳng a, b lần lượt tại các giao điểm là A, B và không cắt đường thẳng c;- Vẽ điểm
Q
∈
c
. Tìm vị trí điểm P sao cho ba điểm O, A, P thẳng hàng và ba điểm P, B, Q thẳng hàng.
Đọc tiếp
Cho trước một điểm O. Em hãy:
- Vẽ ba đường thẳng phân biệt a, b, c đôi một cắt nhau sao cho chúng chỉ có một giao điểm duy nhất là O;
- Vẽ đường thẳng m cắt hai đường thẳng a, b lần lượt tại các giao điểm là A, B và không cắt đường thẳng c;
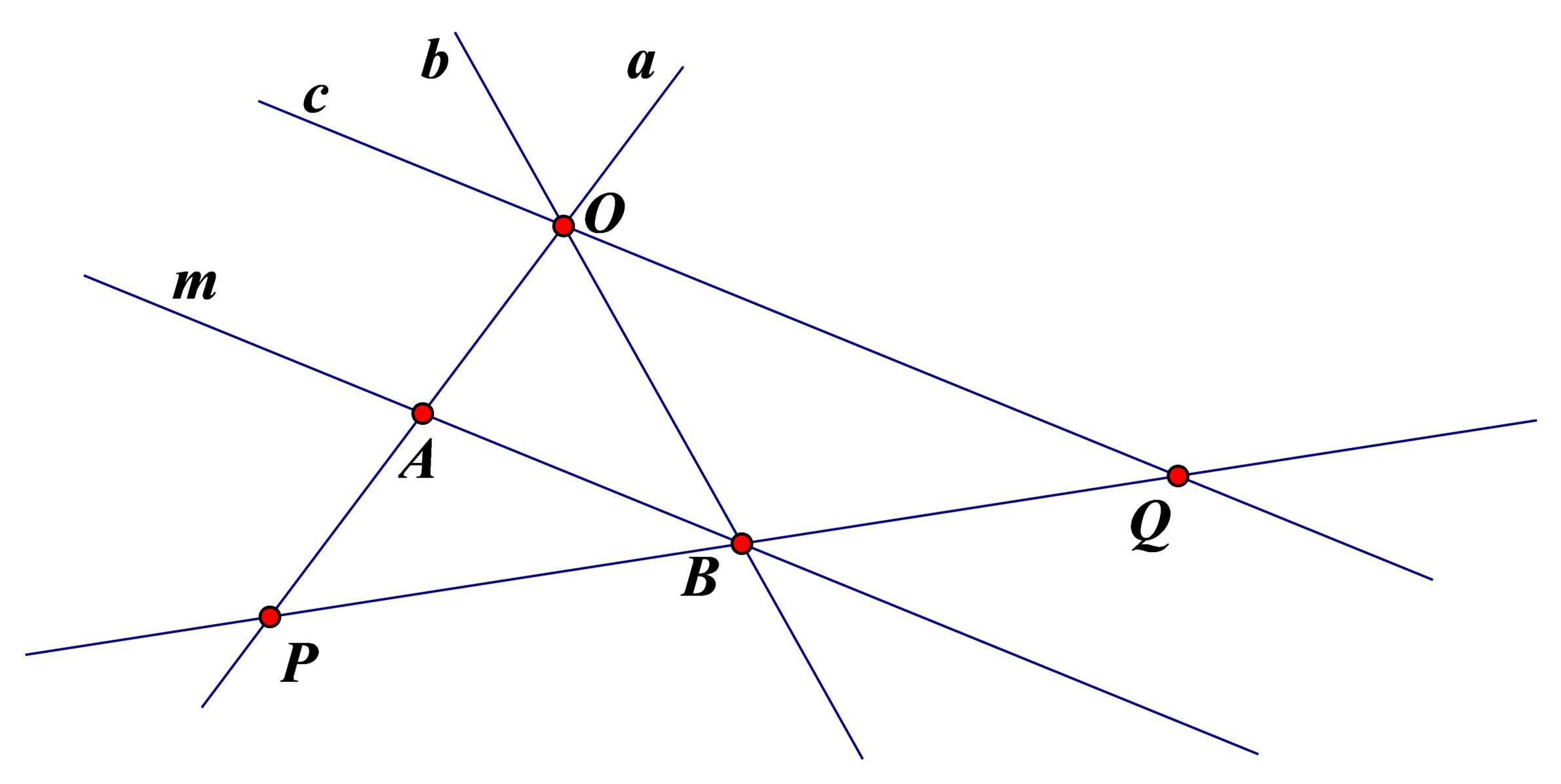
- Vẽ điểm Q ∈ c . Tìm vị trí điểm P sao cho ba điểm O, A, P thẳng hàng và ba điểm P, B, Q thẳng hàng.
P là giao điểm của đường thẳng OA và đường thẳng BQ.
Đúng 0
Bình luận (0)
















