Thay tọa độ điểm A(0;5) vào phương trình đường thẳng  d : y = m x + 5.  ta được:

5=m.0+5 luôn đúng với mọi giá trị của tham số m nên đường thẳng (d) luôn

đi qua điểm A với mọi giá trị của m.

Denta tạo với d1, d2 1 tam giác cân với đỉnh là giao điểm của d1, d2 khi và chỉ khi denta vuông góc phân giác tạo bởi d1, d2

Gọi \(A\left(x;y\right)\) là 1 điểm bất kì thuộc phân giác tạo bởi 2 đường thẳng d1, d2

\(\Rightarrow\dfrac{\left|x-7y+17\right|}{\sqrt{1^2+\left(-7\right)^2}}=\dfrac{\left|x+y-5\right|}{\sqrt{1^2+1^2}}\Leftrightarrow\left|x-7y+17\right|=\left|5x+5y-25\right|\)

\(\Leftrightarrow\left[{}\begin{matrix}5x+5y-25=x-7y+17\\5x+5y-25=-x+7y-17\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x+3y+\dfrac{21}{2}=0\\3x-y-4=0\end{matrix}\right.\)

\(\Rightarrow\Delta\) nhận \(\left(3;-1\right)\) hoặc \(\left(1;3\right)\) là 1 vtpt

Có 2 đường thẳng thỏa mãn:

\(\left[{}\begin{matrix}3\left(x-0\right)-1\left(y-1\right)=0\\1\left(x-0\right)+3\left(y-1\right)=0\end{matrix}\right.\)

a: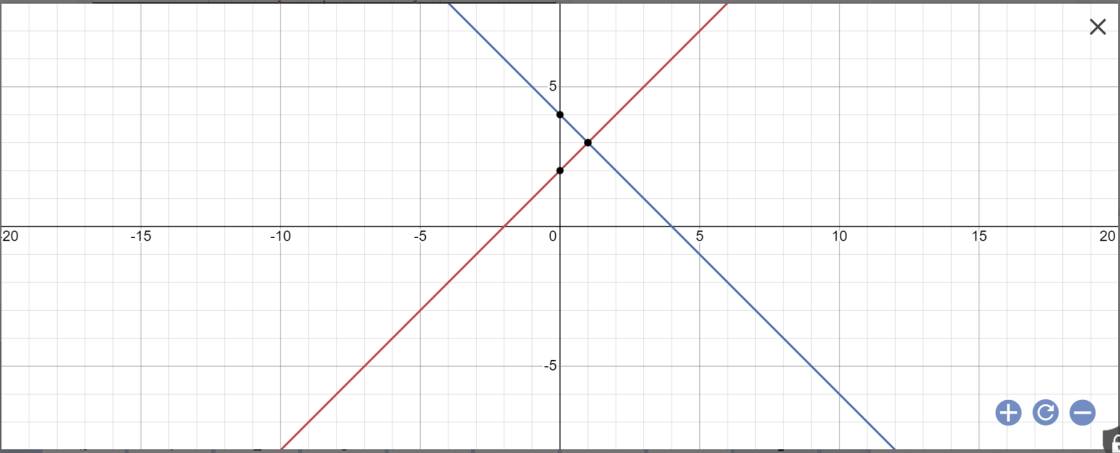 

b: Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)

Thay x=1 và y=3 vào (d3), ta được:

\(1\cdot m+m=3\)

=>2m=3

=>\(m=\dfrac{3}{2}\)

Vì đường thẳng song song với y =3x -5 nên

\(a=3\) Vậy đường thẳng có dạng \(y=3x+b\)

Do đường thẳng đi qua điểm M nên : 

\(-2=3\times-1+b\Leftrightarrow b=1\)

Vậy \(\hept{\begin{cases}a=3\\b=1\end{cases}}\)

h bn thay x=1, y=3 vào phương trình đường thẳng (d)

tìm được m 

hok tốt

Vì \(M\left(1;3\right)\in\left(d\right)\)

\(\Rightarrow3=2m+m-3\)

\(\Leftrightarrow3m=6\)

\(\Leftrightarrow m=2\)

Để đường thẳng \(y=\left(m-2\right)x+k\)  song song với đường thẳng \(y=5x-1.\)

\(\Rightarrow\left\{{}\begin{matrix}m-2=5.\\k\ne-1.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=7.\\k\ne-1.\end{matrix}\right.\)

Đường thẳng \(y=\left(m-2\right)x+k\) đi qua điểm \(P\left(2;1\right).\)

\(\Rightarrow1=\left(7-2\right).2+k.\\ \Leftrightarrow1=10+k.\\ \Leftrightarrow k=-9\left(TM\right).\)

Vậy \(m=7;k=-9.\)

d cách đều MN khi nó thỏa mãn 1 trong 2 trường hợp: d song song MN hoặc d đi qua trung điểm MN

TH1: d song song MN

\(\overrightarrow{MN}=\left(3;-4\right)\Rightarrow d\) nhận (4;3) là 1 vtpt

Phương trình d:

\(4\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow4x+3y-1=0\)

TH2: d đi qua trung điểm MN

Gọi P là trung điểm MN \(\Rightarrow P\left(\dfrac{1}{2};-1\right)\Rightarrow\overrightarrow{AP}=\left(\dfrac{5}{2};-4\right)=\dfrac{1}{2}\left(5;-8\right)\)

\(\Rightarrow d\) nhận (8;5) là 1 vtpt

Phương trình d:

\(8\left(x+2\right)+5\left(y-3\right)=0\Leftrightarrow8x+5y+1=0\)

Có 2 đường thẳng d thỏa mãn: \(\left[{}\begin{matrix}4x+3y-1=0\\8x+5y+1=0\end{matrix}\right.\)