Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+10. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là:
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+1=0. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Tìm điểm N' là ảnh của N(0; 2; 4) quá phép đối xứng qua đường thẳng d.
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng d đi qua điểm A(1;2;1) và vuông góc với mặt phẳng (P): x-2y+z-10 có dạng
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng d đi qua điểm A(1;2;1) và vuông góc với mặt phẳng (P): x-2y+z-1=0 có dạng
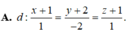
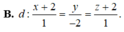
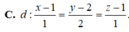
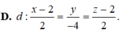
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng
P
:
2
x
+
2
y
-
z
+
9
0
. Đường thẳng d đi qua A và có vectơ chỉ phương
u
→
(
3
;
4
;
-
4
)
cắt (P) tại điểm B. Điểm M thay đổ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng P : 2 x + 2 y - z + 9 = 0 . Đường thẳng d đi qua A và có vectơ chỉ phương u → ( 3 ; 4 ; - 4 ) cắt (P) tại điểm B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc 90 ° . Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?
![]()
![]()
![]()
![]()
Trong không gian với tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng
P
:
2
x
+
2
y
-
z
+
9
0
. Đường thẳng d đi qua A và có vecto chỉ phương
u
→
(
3
;
4
;
-
4
)
cắt (P) tại điểm B. Điểm M thay đổi trong (P) sao...
Đọc tiếp
Trong không gian với tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng P : 2 x + 2 y - z + 9 = 0 . Đường thẳng d đi qua A và có vecto chỉ phương u → ( 3 ; 4 ; - 4 ) cắt (P) tại điểm B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc 90 ° . Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau:
![]()
![]()
![]()
![]()
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có
M
(
2
;
0
)
là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là
7
x
-
2
y
-
3
0
và
6
x
-
y
-
4
0
. Phương trình đường thẳng AC...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M ( 2 ; 0 ) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7 x - 2 y - 3 = 0 và 6 x - y - 4 = 0 . Phương trình đường thẳng AC là
A. 3 x - 4 y - 5 = 0
B. 3 x + 4 y + 5 = 0
C. 3 x - 4 y + 5 = 0
D. 3 x + 4 y - 5 = 0
Trong không gian tọa độ Oxyz cho mặt cầu (S): x2 + y2 + z2 + 4x - 6y + m 0 và đường thẳng Δ là giao tuyến của hai mặt phẳng (α): x + 2y - 2z - 4 0 và (β): 2x - 2y - z + 1 0. Đường thẳng Δ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn AB 8 khi: A. m 12 B. m -12 C. m -10 D. m 5
Đọc tiếp
Trong không gian tọa độ Oxyz cho mặt cầu (S): x2 + y2 + z2 + 4x - 6y + m = 0 và đường thẳng Δ là giao tuyến của hai mặt phẳng (α): x + 2y - 2z - 4 = 0 và (β): 2x - 2y - z + 1 = 0. Đường thẳng Δ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn AB = 8 khi:
A. m = 12
B. m = -12
C. m = -10
D. m = 5
Trong không gian với trục tọa độ Oxyz, cho đường thẳng
∆
:
x
-
1
2
y
-
1
z
+
2
3
và mặt phẳng (
α
): x-2y+2z-30. Đường thẳng đi qua O, vuông góc với
∆
và song song với mặt phẳng (...
Đọc tiếp
Trong không gian với trục tọa độ Oxyz, cho đường thẳng
∆ : x - 1 2 = y - 1 = z + 2 3 và mặt phẳng ( α ): x-2y+2z-3=0.
Đường thẳng đi qua O, vuông góc với ∆ và song song với
mặt phẳng ( α ) có phương trình
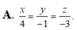
![]()
![]()
![]()
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Viết phương trình tham số của đường thẳng d là giao của (α) và ( β)




