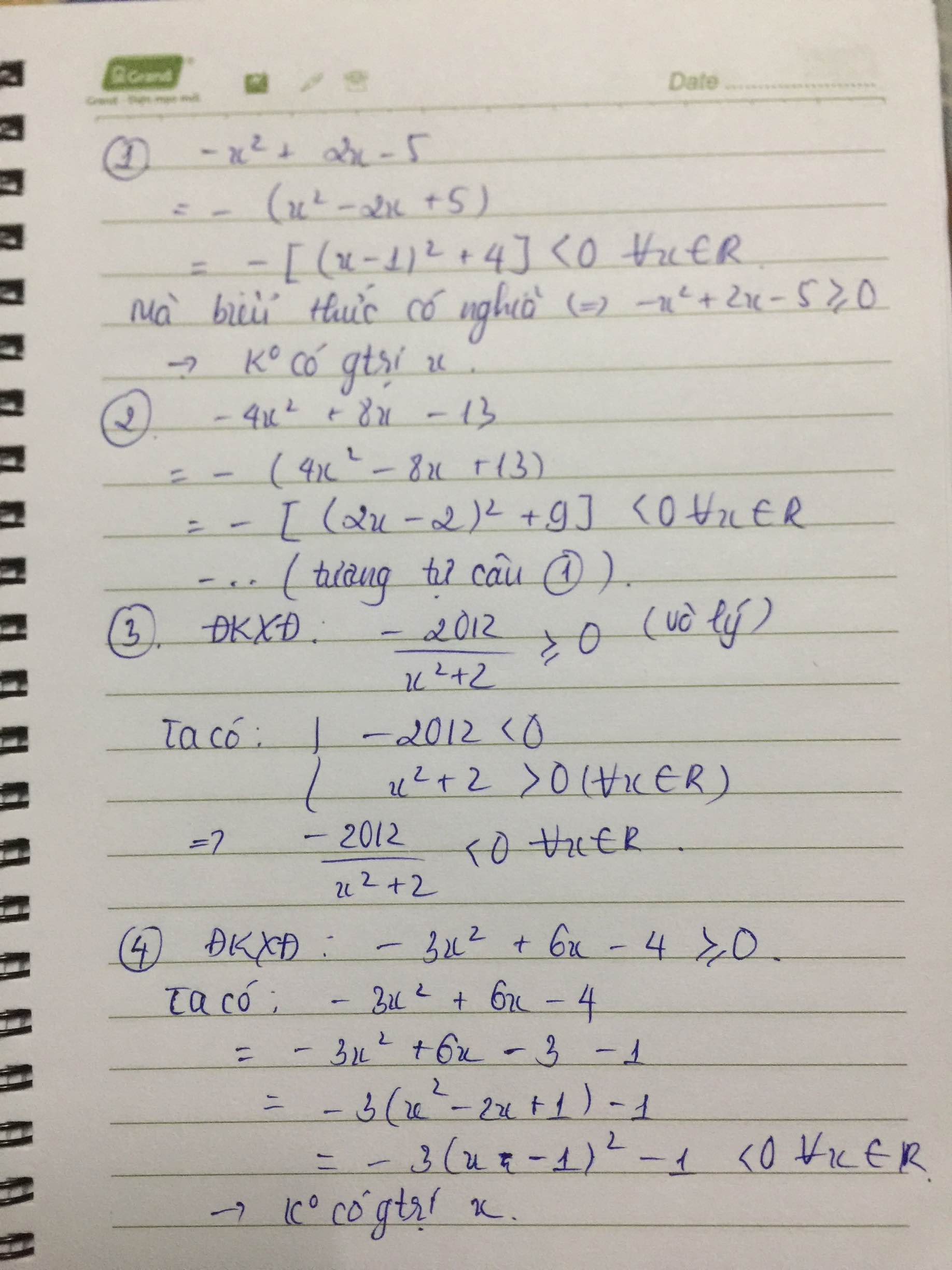chứng minh rằng -8x^4+6x^3-4x^2+2x-1 không có nghiệm nguyên

Những câu hỏi liên quan
Chứng minh rằng \(f\left(x\right)=-8x^4+6x^3-4x^2+2x-1\)không có nghiệm thuộc Z
\(f\left(x\right)=-8x^4+6x^3-4x^2+2x-1\)
\(=-5x^4-\left(3x^4-6x^3+3x^2\right)-\left(x^2-2x+1\right)\)
\(=-5x^4-3\left(x^2-x\right)^2-\left(x-1\right)^2\le0\)
Mà ta dễ thấy dấu = không xảy ra nên f(x) không có nghiệm thuộc Z
Đúng 1
Bình luận (0)
Vì dấu = không xảy ra nên f(x) không có nghiệm z
Đúng 0
Bình luận (0)
Ta dễ thấy dấu "=" không xảy ra nên \(f\left(x\right)\)không có nghiệm của \(Z\)
~~~ Chúc bạn học giỏi ~~~
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Câu 1 : Chứng tỏ rằng đa thức f(x) = -8x4 + 6x3 - 4x2 + 2x - 1 không có nghiệm nguyên
cho đa thức P(x)=x^4-3x^3-4x^2+2x -1. Chứng minh rằng P(x) không có nghiệm là số nguyên
Giả sử đa thức P(x) có nghiệm nguyên
=>P(x) có nghiệm chia hết cho 1 hoặc -1
=>1 và -1 là nghiệm
+) Nếu x=1
⇒P(1)=1^4−3.1^3−4.1^2−2.1−1⇒P(1)=1^4-3.1^3-4.1^2-2.1-1
⇒P(1)=1−3.1−4.1−2.1−1⇒P(1)=1-3.1-4.1-2.1-1
⇒P(1)=1−3−4−2−1⇒P(1)=1-3-4-2-1
⇒P(1)=−9≠0⇒P(1)=-9≠0
⇒x=1 không phải là nghiệm của P(x)P(x)
+) Nếu x=−1
⇒P(−1)=(−1)^4−3.(−1)^3−4.(−1)^2−2.(−1)−1⇒P(-1)=(-1)^4-3.(-1)^3-4.(-1)^2-2.(-1)-1
⇒P(−1)=1−3.(−1)−4.1−(−2)−1⇒P(-1)=1-3.(-1)-4.1-(-2)-1
⇒P(−1)=1+3−4+2−1⇒P(-1)=1+3-4+2-1
⇒P(−1)=1≠0⇒P(-1)=1≠0
⇒x=−1 không phải là nghiệm của P(x)P(x)
Vậy P(x) không có nghiệm là số nguyên
Đúng 1
Bình luận (0)
Chứng minh rằng không tồn tại x để các biểu thức có nghĩa
1.\(\sqrt{-x^2+2x-5}\)
2.\(\sqrt{-4x^2+8x-13}\)
3.\(\sqrt{\dfrac{-2012}{x^2+2}^{ }}\)
4.\(\sqrt{\dfrac{-3x^2+6x-4}{5}}\)
a, \(-x^2+2x-5=-\left(x^2-2x+5\right)=-\left(x^2-2x+1+4\right)\)
\(=-\left[\left(x-1\right)^2+4\right]\)
do \(\left(x-1\right)^2\ge0=>\left(x-1\right)^2+4\ge4=>-\left[\left(x-1\right)^2+4\right]\le-4< 0\)
Vậy ko tồn tại..........
b, \(-4x^2+8x-13=-4\left(x^2-2x+\dfrac{13}{4}\right)\)
\(=-4\left[x^2-2x+1+\dfrac{9}{4}\right]=-4\left[\left(x-1\right)^2+\dfrac{9}{4}\right]\le-9< 0\)
vậy....
c, \(\dfrac{-2021}{x^2+2}\) do \(x^2+2>2=>\dfrac{-2012}{x^2+2}< -1006< 0\)
vậy,,,,,,,,,,
d, \(-3x^2+6x-4=-3\left(x^2-2x+\dfrac{4}{3}\right)=-3\left(x^2-2x+1+\dfrac{1}{3}\right)\)
\(=-3\left[\left(x-1\right)^2+\dfrac{1}{3}\right]\le-1< 0\)
vậy...
Đúng 3
Bình luận (0)
chứng minh rằng đa thức :f(x)=-4x4+3x3-2x2+x-1 không có nghiệm nguyên
Chứng minh rằng giá trị của biểu thức (2x - 1)(8x - 3) – (4x - 1)² + 6x không phụ thuộc vào giá trị của x.
Lời giải:
$(2x-1)(8x-3)-(4x-1)^2+6x=16x^2-6x-8x+3-(16x^2-8x+1)+6x$
$=16x^2-14x+3-16x^2+8x-1+6x$
$=(16x^2-16x^2)+(-14x+8x+6x)+(3-1)=0+0+2=2$ là giá trị không phụ thuộc vào biến $x$
Đúng 1
Bình luận (0)
Bài 1: Cho đa thức bậc nhất: f(x) ax + b và g(x) bx + a (a và b khác 0). Giả sử đa thức f(x) có nghiệm là x0, tìm nghiệm của đa thức g(x)Bài 2: Chứng tỏ rằng f(x) -8x4 + 6x3 - 4x2 + 2x - 1 không có nghiệm nguyên.Bài 3: Cho đa thức f(x) ax3 + bx2 + cx + d có giá trị nguyên với mọi x thuộc Z. Chứng tỏ rằng 6a và 2b là các số nguyên
Đọc tiếp
Bài 1: Cho đa thức bậc nhất: f(x) = ax + b và g(x) = bx + a (a và b khác 0). Giả sử đa thức f(x) có nghiệm là x0, tìm nghiệm của đa thức g(x)
Bài 2: Chứng tỏ rằng f(x) = -8x4 + 6x3 - 4x2 + 2x - 1 không có nghiệm nguyên.
Bài 3: Cho đa thức f(x) = ax3 + bx2 + cx + d có giá trị nguyên với mọi x thuộc Z. Chứng tỏ rằng 6a và 2b là các số nguyên
T(x) = 6x4 - 13x - 3
H(x) = 8x4 + 2x3 -17x +1
a) Tìm nghiệm của T(x) và chứng minh H(x) không có nghiệm âm
b) Chứng minh rằng H(x) vô nghiệm với mọi giá trị x.
Chứng minh rằng đa thức: f(x)=3x3-2x2+4x+1 không có nghiệm nguyên.