Toán hình học về góc vuông

Những câu hỏi liên quan
Hôm nay Bờm lại được học toán học về hình thang cân.Ví dụ ABCD là hình thang cân có cạnh AB//CD,ADBC và gọi M,N lần lượt là trung điểm của AB,CD thì M,N vuông góc với AB,CD.Thầy giáo có một bài toán đố Bờm như sau :Cho X,Y,Z,T là bốn góc (đơn vị đo độ).Hỏi 4 góc X,Y,Z,T có phải 4 góc của hình thang cân hay không Nhập vào 4 số X, Y, Z, T (điều kiện luôn nhập vào |X|, |Y|, |Z|, |T|10^9. Hãy in ra từ YES nếu nó là 4 góc của hình thang cân, ngược lại in ra NO(C++)
Đọc tiếp
Hôm nay Bờm lại được học toán học về hình thang cân.Ví dụ ABCD là hình thang cân có cạnh AB//CD,AD=BC và gọi M,N lần lượt là trung điểm của AB,CD thì M,N vuông góc với AB,CD.Thầy giáo có một bài toán đố Bờm như sau :Cho X,Y,Z,T là bốn góc (đơn vị đo độ).Hỏi 4 góc X,Y,Z,T có phải 4 góc của hình thang cân hay không Nhập vào 4 số X, Y, Z, T (điều kiện luôn nhập vào |X|, |Y|, |Z|, |T|<=10^9. Hãy in ra từ YES nếu nó là 4 góc của hình thang cân, ngược lại in ra NO(C++)
#include<iostream>
#include<cmath>
using namespace std;
int main() {
double x, y, z, t;
double pi = acos(-1.0);
double a, b, c, d;
cin >> x >> y >> z >> t;
double alpha = x * pi / 180, beta = y * pi / 180;
double gamma = z * pi / 180, delta = t * pi / 180;
double distance = cos(alpha) + cos(beta) + cos(gamma) + cos(delta);
if (distance == 2) {
cout << "YES" << endl;
} else {
cout << "NO" << endl;
}
return 0;
}
Đúng 0
Bình luận (0)
BÀI TOÁN VỀ HÌNH HỌC LỚp 7
Cho tam giác ABC vuông tại A(AB>AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Vẽ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm E sao cho HE=HA. Chứng minh AE vuông góc với ED
chưa chị nhưng em đã biết rồi nên chị mà biết thì chỉ cho e
Đúng 0
Bình luận (0)
suy ra HM là đường trung bình của tam giác AED
suy ra HM song song với ED
mặt khác AH vuông góc với HM nên AE vuông góc với HM
từ HM song song với ED và AE vuông góc với HM
suy ra AE vuông góc với ED(đpcm)
Đúng 0
Bình luận (0)
Học sinh vẽ lại hình, viết giả thiết kết luận và trình bày lời giải bài toán sau: Cho hình vẽ bên Biết b vuông góc c; 𝐴̂1 = 550; 𝐵̂1 = 550𝐶̂1 = 1200a) Chứng minh: a //b b) Chứng minh: a vuông góc c c) Tính số đo 𝐵𝑂𝐶 ̂
vì c cắt a và b tạo thành cặp vuông góc bằng nha
⇒ a//b
Đúng 1
Bình luận (0)
à nhớ chứng minh là AB cắt a và b taoh thành cặp góc đồng vị bằng nhau
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình với ạ!
Cho tam giác vuông có tỉ số giữa hai cạnh góc vuông là 3:4. Nếu giảm chiều
dài 2 m và giữ nguyên chiều rộng thì được một tam giác vuông mới có diện tích
bằng 75% diện tích tam giác vuông ban đầu. Tính độ dài cạnh góc vuông bé hơn.
Đây là toán 8 (Mình nghĩ là toán 8 vì cô mình đăng bt này là toán 8 chương 4 đại số, toán thực tế có yếu tố hình học).
gọi \(x\) là độ dài cạnh góc vuông bé hơn \((x>0)\)
cạnh góc vuông lớn hơn là \(\frac{4x}{3}\)
diện tích tam giác vuông ban đầu là \((x\times\frac{4x}{3})\div2=\frac{2x^2}{3}\)
theo đề ra ta có phương trình
\((\frac{4x}{3}-2)\times x=\frac{2x^2}{3}\times75\div100\)
giải phương trình ta được \(\orbr{\begin{cases}x=0(ktm)\\x=2,4\end{cases}}\)
Nhiệm vụ 1: Học thuộc định lý, viết 4 hệ thức về cạnh và góc trong tam giác vuông.Nhiệm vụ 2: Hãy đặt ra một bài toán cho biết cạnh huyền và một góc nhọn của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy.Nhiệm vụ 3: Hãy đặt ra một bài toán cho biết 2 cạnh của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy. Nhiệm vụ 4: Tìm hiểu thế nào là giải tam giác vuông?
Đọc tiếp
Nhiệm vụ 1: Học thuộc định lý, viết 4 hệ thức về cạnh và góc trong tam giác vuông.
Nhiệm vụ 2: Hãy đặt ra một bài toán cho biết cạnh huyền và một góc nhọn của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy.
Nhiệm vụ 3: Hãy đặt ra một bài toán cho biết 2 cạnh của tam giác vuông, yêu cầu tính các cạnh và góc còn lại của tam giác vuông ấy. Nhiệm vụ 4: Tìm hiểu thế nào là giải tam giác vuông?
Cho hình thoi ABCD, E là giao điểm 2 đường chéo, kẻ EI vuông góc với AD tại I. Gọi K là trung điểm của EI
Chứng minh CI vuông góc với DK
(Đây là toán 8 học kỳ I, không sử dụng được tam giác đồng dạng)
giải cho tôi bài toán này theo cách của học sinh lớp 8 : cho tam giác ABC vuông tại A có ABAC , đường cao AH từ H kẻ HM vuông góc với AB ( M thuộc AB ) kẻ HN vuông góc AC ( N thuộc AC )
a, tứ giác AMHN là hình gì ? vì sao ?
b, Y là trung điểm của HC , K là 1 điểm sao cho Y là trung điểm của KA . chứng minh AC song song với HK
c , chứng minh tứ giác MNCK là hình thang cân
d, MN cắt AH tại O , CO cắt AK tại D . chứng minh AK 3AD
Đọc tiếp
giải cho tôi bài toán này theo cách của học sinh lớp 8 : cho tam giác ABC vuông tại A có AB<AC , đường cao AH từ H kẻ HM vuông góc với AB ( M thuộc AB ) kẻ HN vuông góc AC ( N thuộc AC )
a, tứ giác AMHN là hình gì ? vì sao ?
b, Y là trung điểm của HC , K là 1 điểm sao cho Y là trung điểm của KA . chứng minh AC song song với HK
c , chứng minh tứ giác MNCK là hình thang cân
d, MN cắt AH tại O , CO cắt AK tại D . chứng minh AK = 3AD
*(8GP) Trích Câu 39, mã đề 115, đề kiểm tra giữa học kì II, môn Toán không chuyên, lớp 12, năm học 2022-2023, trường THPT Chu Văn An - Hà Nội:Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD 2a, cạnh bên SA vuông góc với đáy và SA a. Gọi M là trung điểm của cạnh AD và (S) là mặt cầu ngoại tiếp hình tứ diện SCDM. Bán kính của (S) bằng:A. dfrac{3}{2}B. dfrac{sqrt{11}}{2}C. dfrac{sqrt{14}}{2}D. dfrac{sqrt{26}}{2} *Câu hỏi phụ: Liệu rằng, đơn vị của bán kính (S) trong 4 đáp án trên đã...
Đọc tiếp
*(8GP) Trích Câu 39, mã đề 115, đề kiểm tra giữa học kì II, môn Toán không chuyên, lớp 12, năm học 2022-2023, trường THPT Chu Văn An - Hà Nội:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, cạnh bên SA vuông góc với đáy và SA = a. Gọi M là trung điểm của cạnh AD và (S) là mặt cầu ngoại tiếp hình tứ diện SCDM. Bán kính của (S) bằng:
A. \(\dfrac{3}{2}\)
B. \(\dfrac{\sqrt{11}}{2}\)
C. \(\dfrac{\sqrt{14}}{2}\)
D. \(\dfrac{\sqrt{26}}{2}\)
*Câu hỏi phụ: Liệu rằng, đơn vị của bán kính (S) trong 4 đáp án trên đã chính xác? Và liệu bán kính (S) có luôn bằng 1 trong 4 đáp án trên với mọi giá trị của a và thuộc tính hình khi thay đổi?
Mình sẽ trao 8GP cho bạn nào trả lời đúng đáp án, giải thích câu hỏi chính cũng như trả lời thuyết phục những câu hỏi phụ. Em cũng rất mong các anh chị giáo viên Toán hoc24 sẽ giúp em giải đáp thắc mắc câu hỏi phụ ạ.
Cách tính bài này đơn giản là tọa độ hóa nó (tứ diện cần tính ko đặc biệt, nhưng chóp ban đầu thì tọa độ hóa được), gọi A là gốc (0,0,0), quy ước a là 1 đơn vị độ dài, các tia AS, AB, AD lần lượt là Oz, Oy, Ox, ta có các tọa độ \(S\left(0,0,1\right)\); M(1,0,0), D(2,0,0), C(2,1,0), \(I\left(x;y;z\right)\) là tâm
\(SI=CI=DI=MI\Rightarrow\left\{{}\begin{matrix}x^2+y^2+\left(z-1\right)^2=\left(x-1\right)^2+y^2+z^2\\x^2+y^2+\left(z-1\right)^2=\left(x-2\right)^2+y^2+z^2\\x^2+y^2+\left(z-1\right)^2=\left(x-2\right)^2+\left(y-1\right)^2+z^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-z=0\\4x-2z=3\\4x+2y-2z=4\end{matrix}\right.\) \(\Rightarrow I\left(\dfrac{3}{2};\dfrac{1}{2};\dfrac{3}{2}\right)\)
\(\Rightarrow R=SI=\dfrac{\sqrt{11}}{2}\)
Do quy ước a là 1 đơn vị độ dài nên đáp án chính xác là \(R=\dfrac{a\sqrt{11}}{2}\)
Lý do đáp án chỉ có số mà thiếu a: theo tư duy của mình thì người ra đề mang hướng giải y như mình bên trên, tức là quy ước độ dài rồi tọa độ hóa, nhưng khi đưa ra đáp án cuối cùng lại quên chuyển từ quy ước về đơn vị thực nên thiếu a. Về cơ bản là người ta quên, ko có gì bí ẩn đáng suy nghĩ ở đây cả :D. Kích thước là a thì mọi kích thước độ dài sẽ phụ thuộc a.
Đúng 3
Bình luận (2)
canh đêm đăng r mà vẫn có ng đăng huhu
Đúng 0
Bình luận (4)
Chào Quoc Tran Anh Le,
Ta có thể giải bài toán bằng cách sử dụng định lý Pythagoras và định lý đồng quy của tứ diện.
Đặt $O$ là tâm của mặt cầu $(S)$, ta cần tìm bán kính $R=OS$. Gọi $H$ là trung điểm của $SC$.
Ta có $OH \perp SC$ và $OH$ cắt $SC$ tại $E$, ta cần tìm $OE=R-OS$. Khi đó ta có $OH^2 = OE^2 + HE^2$, hay $R^2-2R\times OS + OS^2 = OH^2 = OH^2= SA^2 + AH^2 = a^2 + \left(\dfrac{a}{2}\right)^2 = \dfrac{5a^2}{4}$.
Từ đó suy ra: $$OS^2 = \dfrac{5a^2}{4}-\dfrac{a^2}{4} = a^2$$
Vậy $OS = a$ và $R=\sqrt{2}a$.
Đáp án là $\textbf{(D)}\ \sqrt{\frac{26}{2}}$.
Câu hỏi phụ:
Đơn vị của bán kính trong 4 đáp án đều là đơn vị độ dài, do đó đơn vị này không được nêu rõ trong đề bài.Khi thay đổi giá trị của $a$, bán kính $(S)$ cũng thay đổi theo và không luôn bằng $1$.
Đúng 1
Bình luận (0)
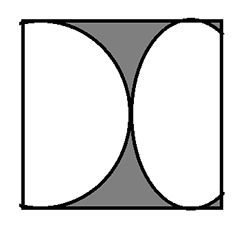
Cho hình vuông ABCD. Vẽ 2 nửa hình tròn đường kính AD, BC (bạn tự hình dung nhé). Biết chu vi đường tròn đường kính AD - 25,12cm. Tính diện tích phần tô đậm.
Đọc tiếp
Cho hình vuông ABCD. Vẽ 2 nửa hình tròn đường kính AD, BC (bạn tự hình dung nhé). Biết chu vi đường tròn đường kính AD - 25,12cm. Tính diện tích phần tô đậm.
| Nhật Tân |
| Chủ nhật, ngày 28/01/2018 06:13:29 |

Đúng 0
Bình luận (0)






















