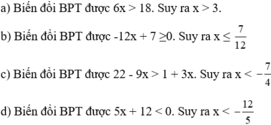Giải các bất phương trình a (x-1)(2-x)>0 b x2 -4x+3

Những câu hỏi liên quan
Giải các bất phương trình sau:a)
2
x
−
7
11
−
4
x
;
b)
x
−
2
2
−
x
2
−
8
x
+
3
≥
0
;
c)
2
3
−
3...
Đọc tiếp
Giải các bất phương trình sau:
a) 2 x − 7 > 11 − 4 x ; b) x − 2 2 − x 2 − 8 x + 3 ≥ 0 ;
c) 2 3 − 3 x − 6 2 > 1 + 3 x 6 ; d) x − 5 x + 1 + 4 x + 3 < − 5 x 2
bài 1 giải các bất phương trình sau
a, -x2 +5x-6 ≥ 0
b, x2-12x +36≤0
c, -2x2 +4x-2≤0
d, x2 -2|x-3| +3x ≥ 0
e, x-|x+3| -10 ≤0
bài 2 xét dấu các biểu thức sau
a,<-x2+x-1> <6x2 -5x+1>
b, x2-x-2/ -x2+3x+4
c, x2-5x +2
d, x-< x2-x+6 /-x2 +3x+4 >
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
Đúng 0
Bình luận (0)
Giải các bất phương trình sau:
a) -2x2 + 7x - 10 < 0
b) \(\dfrac{1+x}{1-x}\) ≤ 2
c) \(\dfrac{x}{x-2}-\dfrac{2}{x-3}\) > 1
d) (x2 + 4x + 10)2 - 7(x2 + 4x + 11) + 7 < 0
Giải các bất phương trình sau
a) (x2+2)2-(x+2)(x-2)(x2+4)-4x(x+1)< hoặc = 20
b) (x+2)(x2-2x+4)-x(x2+2)> hoặc = 15
a) \(\left(x^2+2\right)^2-\left(x+2\right)\left(x-2\right)\left(x^2+4\right)-4x\left(x+1\right)\le20\)
\(\Leftrightarrow x^4+4x^2+4-x^4+16-4x^2-4x\le20\)
\(\Leftrightarrow\left(x^4-x^4\right)+\left(4x^2-4x^2\right)-4x+4+16\le20\)
\(\Leftrightarrow-4x+20\le20\)
\(\Leftrightarrow-4x\le20-20\)
\(\Leftrightarrow-4x\le0\)
\(\Leftrightarrow-4x:-4\ge0:-4\)
\(\Leftrightarrow x\ge0\)
Vậy nghiệm của bất phương trình là: \(x\ge0\)
b) \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2+2\right)\ge15\)
\(\Leftrightarrow x^3+8-x^3-2x\ge15\)
\(\Leftrightarrow\left(x^3-x^3\right)+8-2x\ge15\)
\(\Leftrightarrow8-2x\ge15\)
\(\Leftrightarrow-2x\ge15-8\)
\(\Leftrightarrow-2x\ge7\)
\(\Leftrightarrow-2x:-2\le7:-2\)
\(\Leftrightarrow x\le-\dfrac{7}{2}\)
Vậy nghiệm của bất phương trình là \(x\le-\dfrac{7}{2}\)
Đúng 3
Bình luận (0)
a: =>x^4+4x^2+4-x^4+16-4x^2-4x<=20
=>-4x+20<=20
=>-4x<=0
=>x>=0
b: =>x^3+8-x^3-2x>=15
=>-2x>=7
=>x<=-7/2
Đúng 0
Bình luận (0)
Giải các bất phương trình
g
(
x
)
≤
0
v
ớ
i
g
(
x
)
x
2
-
5
x
+
4
x...
Đọc tiếp
Giải các bất phương trình g ' ( x ) ≤ 0 v ớ i g ( x ) = x 2 - 5 x + 4 x - 2
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Đúng 1
Bình luận (0)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
Đúng 1
Bình luận (0)
giải các bất phương trình sau
a, <x-3>*<x2+x-20>≥0
b, x2-4x-5 /2x+4 ≥0
c, -1/x2-6x+8≤1
a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)
\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)
+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)
\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))
b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)
+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))
c, \(\dfrac{-1}{x^2-6x+8}\le1\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))
Chúc bn học tốt!
Đúng 2
Bình luận (0)
giải các Phương trình sau
a) (5x+3)(x2+1)(x-1)=0
b) (4x-1)(x-3)-(x-3)(5x+2)=0
c) (x+6)(3x-1)+x2-36 =0
a: =>(5x+3)(x-1)=0
=>x=1 hoặc x=-3/5
b: =>(x-3)(4x-1-5x-2)=0
=>(x-3)(-x-3)=0
=>x=-3 hoặc x=3
c: =>(x+6)(3x-1+x-6)=0
=>(x+6)(4x-7)=0
=>x=7/4 hoặc x=-6
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
2
–l0x -25; b) 4
x
2
- 4x -1;c)
(
1
-
2
x
)
2
(
3
x
-
2...
Đọc tiếp
Giải các phương trình sau:
a) x 2 –l0x = -25; b) 4 x 2 - 4x = -1;
c) ( 1 - 2 x ) 2 = ( 3 x - 2 ) 2 ; d) ( x - 2 ) 3 + ( 5 - 2 x ) 3 =0.
a) x = 5. b) x = 1 2 .
c) x = 3 5 hoặc x = 1. d) x = 3.
Đúng 0
Bình luận (0)
\(a,x^2-10x=-25\)
\(< =>x^2-10x+25=0\)
\(< =>\left(x-5\right)^2=0< =>x=5\)
b, \(4x^2-4x=-1\)
\(< =>4x^2-4x+1=0\)
\(< =>\left(2x-1\right)^2=0< =>x=\frac{1}{2}\)
c,\(\left(1-2x\right)^2=\left(3x-2\right)^2\)
\(< =>\left(1-2x\right)^2-\left(3x-2\right)^2=0\)
\(< =>\left(1-2x-3x+2\right)\left(1-2x+3x-2\right)=0\)
\(< =>\left(-5x+3\right)\left(x-1\right)=0\)
\(< =>\orbr{\begin{cases}x=\frac{3}{5}\\x=1\end{cases}}\)
d, \(\left(x-2\right)^3+\left(5-2x\right)^3=0\)
\(< =>\left(x-2+5-2x\right)\left(x^2-4x+4+5x-2x^2-10+4x+25-20x+4x^2\right)=0\)
\(< =>\left(3-x\right)\left(-5x^2-15x+19\right)=0\)
\(< =>\left(x-3\right)\left(5x^2+15x-19=0\right)\)
\(< =>\orbr{\begin{cases}x=3\\x^2+3x-\frac{19}{5}=0\end{cases}}\)
Xét phương trình \(x^2+3x-\frac{19}{5}=0< =>\left(x^2+2.x.\frac{3}{2}+\frac{9}{4}\right)-\left(\frac{19}{5}+\frac{9}{4}\right)=0\)
\(< =>\left(x+\frac{3}{2}\right)^2=\frac{29}{5}+\frac{1}{4}\)
\(< =>\orbr{\begin{cases}x=\sqrt{\frac{29}{5}+\frac{1}{4}}-\frac{3}{2}\\x=-\sqrt{\frac{29}{5}+\frac{1}{4}}-\frac{3}{2}\end{cases}}\)
Vậy .........
Xem thêm câu trả lời