giá trị nào của m thì đường thẳng (d) y=3/2x+2m cắt (p) y=-3/4x2 tại 2 điểm phân biệt

Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên dương của tham sốnm để đường thẳng y=(m+2)x+7-2m cắt parapol y=2x² tại hai điểm phân biệt nằm về hai phía của trục tung : A.4 B.2 C.1 D.3
Cho hàm số y = 2 x + 3 x + 2 có đồ thị (C) và đường thẳng d ; y = x + m. Với giá trị nào của tham số m thì d cắt (C) tại hai điểm phân biệt?
A. m < -2
B. m < 2 hoặc m > 6
C. 2 < m < 6
D. m < -6
Đáp án B
2 x + 3 x + 2 = x + m ⇔ 2 x + 3 = x 2 + m x + 2 x + 2 m ⇔ f x = x 2 + m x + 2 m - 3 = 0 ( 1 )
Rõ ràng f - 2 ≠ 0 , ∀ m nên ta cần có ∆ > 0 ⇔ m 2 - 4 2 m - 3 > 0 ⇔ [ m > 6 m < 2 .
Đúng 0
Bình luận (0)
Với giá trị nào của k thì đường thẳng (d):\(y=-3x+2k-3\) cắt parabol (P): y = \(x^2\) tại hai điểm phân biệt.
Lời giải:
Để $(d)$ cắt $(P)$ tại hai điểm phân biệt thì PT hoành độ giao điểm $x^2-(3x+2k-3)=x^2-3x+(3-2k)=0$ có 2 nghiệm phân biệt
Điều này xảy ra khi mà:
$\Delta=9-4(3-2k)>0$
$\Leftrightarrow -3+8k>0$
$\Leftrightarrow k> \frac{3}{8}$
Đúng 0
Bình luận (0)
Hàm số
y
x
3
+
3
x
2
-
2
Với các giá trị nào của m thì đồ thị hàm số cắt đường thẳng d : y m tại 3 điểm phân biệt?` A.
-
2
m
0
B.
0
m
2
C.
-
2
m
2
D.
m
-
2
∨
m...
Đọc tiếp
Hàm số y = x 3 + 3 x 2 - 2 Với các giá trị nào của m thì đồ
thị hàm số cắt đường thẳng d : y = m tại 3 điểm phân
biệt?`
A. - 2 < m < 0
B. 0 < m < 2
C. - 2 < m < 2
D. m < - 2 ∨ m > 2
Cho parabol (P): y=x và đường thẳng (d): y =2mx−m’ +2m+1 a) Vẽ (P). b) Với giá trị nào của m thì (P) và (d) cắt nhau tại hai điểm phân biệt cùng nằm bên phải trục tung.
Trong mptđ Oxy, cho: parabol (P): \(y=x^2\) và đường thẳng (d): \(y=\left(m-1\right)x+m^2-2m+3\)
.Cm (d) luôn cắt (P) tại 2 điểm phân biệt với mọi giá trị của m
PTHĐGĐ là:
x^2-(m-1)x-m^2+2m-3=0
a*c=-m^2+2m-3=-(m^2-2m+3)
=-(m^2-2m+1+2)
=-(m-1)^2-2<0
=>(P) luôn cắt (d) tại hai điểm phân biệt
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
–
4
x
2
-
2
có đồ thị (C) và đường thẳng
d
:
y
m
.
Tất cả các giá trị của tham số m để d cắt (C) tại bốn điểm phân biệt là A.
-
6
≤
m
≤
2
B. 2 m 6 C. -6 m -2 D. ...
Đọc tiếp
Cho hàm số y = x 4 – 4 x 2 - 2 có đồ thị (C) và đường thẳng d : y = m . Tất cả các giá trị của tham số m để d cắt (C) tại bốn điểm phân biệt là
A. - 6 ≤ m ≤ 2
B. 2 < m < 6
C. -6 < m < -2
D. 2 ≤ m ≤ 6
Chọn C.
Xét hàm số y = x4- 4x2 - 2
Tính y’ = 4x3 – 8x
![]()
Bảng biến thiên:
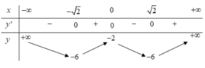
Dựa vào bảng biến thiên suy ra để đồ thị hàm số (C) cắt d tại 4 điểm phân biệt khi và chỉ khi: - 6 < m < -2.
Đúng 0
Bình luận (0)
Cho 2 hàm số:
(P):y=x2
(D):y=2x+m
với giá trị nào của m thì đường thẳng(D)
a)không cắt pa-ra-bol
b)tiếp xúc với pa-ra-bol(P)?tìm tọa độ tiếp điểm?
c)cắt pa-ra-bol(P) tại 2 điểm phân biệt
Phương trình hoành độ giao điểm là:
\(x^2-2x+m=0\)
\(\text{Δ}=\left(-2\right)^2-4m=-4m+4\)
a: Để (d) không cắt (P) thì -4m+4<0
=>-4m<-4
hay m>1
b: Để (d) tiếp xúc với (P) thì 4-4m=0
hay m=1
c: Để (d) cắt (P) tại hai điểm phân biệt thì -4m+4>0
=>-4m>-4
hay m<1
Đúng 3
Bình luận (0)
a, Giải hệ phương trình:
x
+
1
y
-
1
x
y
-
1...
Đọc tiếp
a, Giải hệ phương trình: x + 1 y - 1 = x y - 1 x - 3 y - 3 = x y - 3
b, Trên mặt phẳng tọa độ Oxy, cho prabol (P): y = x 2 và đường thẳng d: y = 2 x + m 2 - 2 m . Tìm các giá trị của m để d cắt (P) cắt tại hai điểm phân biệt nằm về hai phía của trục tung Oy
a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 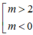
Kết luận 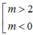
Đúng 0
Bình luận (0)












