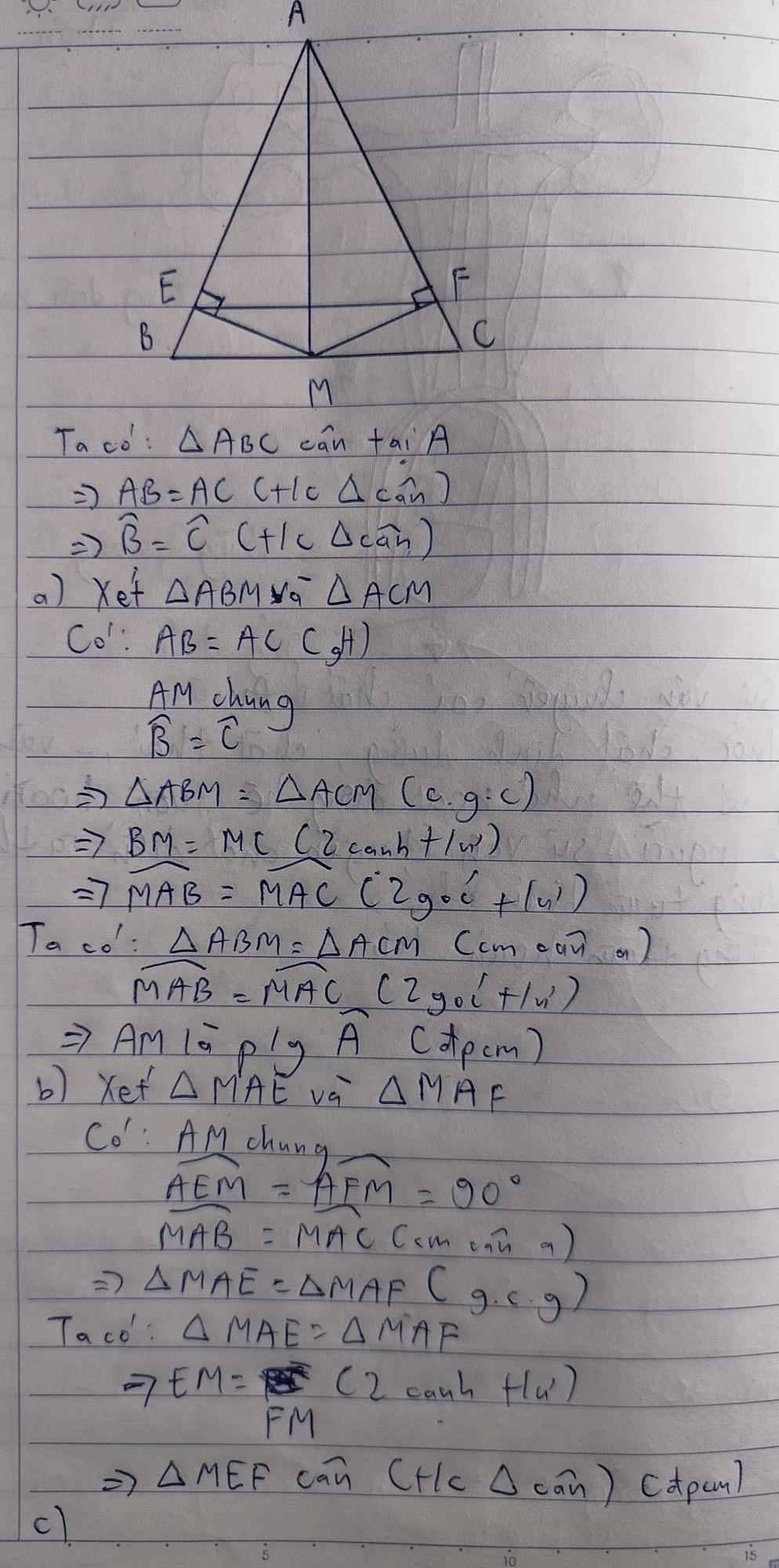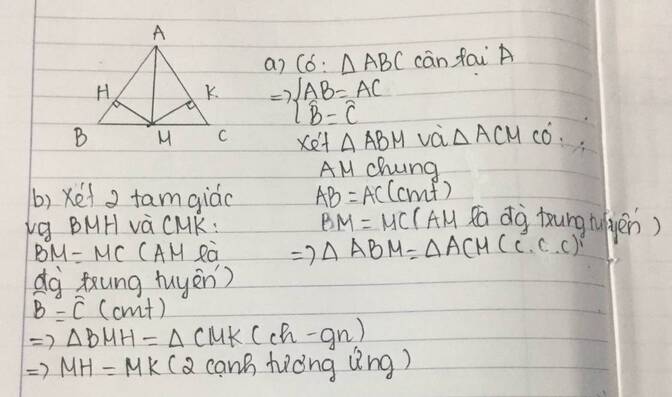/ Cho tam giác ABC cân tại A có đường trung tuyến AM . Chứng minh tam giác ABM = tam giác ACM

Những câu hỏi liên quan
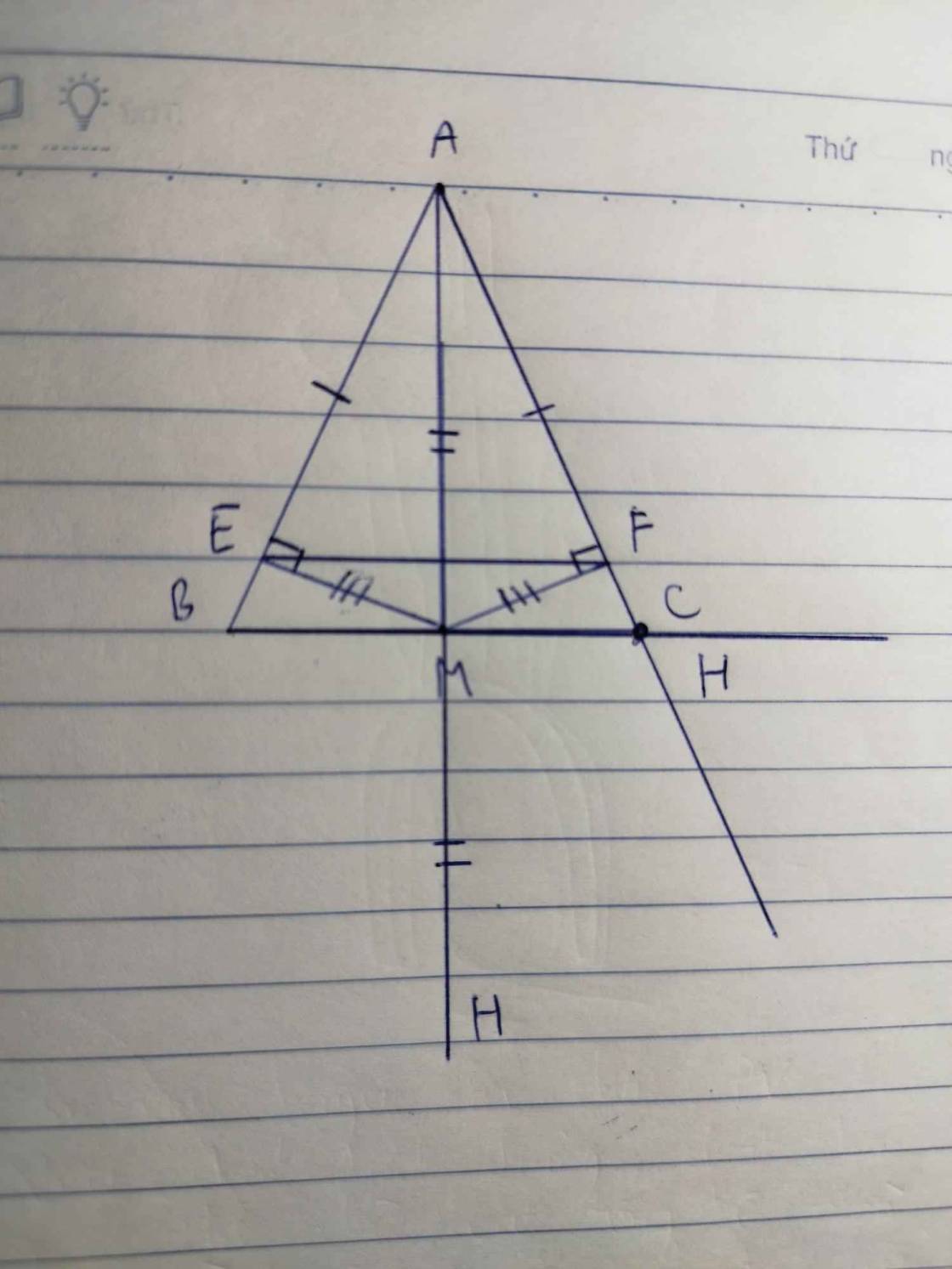
cho tam giác ABC cân tại A (A nhỏ hơn 90 độ có AM là đường trung tuyến)a) chứng minh tam giác ABM tam giác ACM và AM là tia phân giác góc Ab) từ M vẽ ME vuông góc với AB tại E; MF vuông góc với AC tại F, chứng minh tam giác MAE tam giác MAF và tam giác MEF cânc) trên tia đối của tia MA lấy điểm H sao cho MAMH, gọi M là trung điểm (H,y là giao điểm của CB và AN) chứng minh BC bằng 6 lần MIcần gấp ạ!!
Đọc tiếp
cho tam giác ABC cân tại A (A nhỏ hơn 90 độ có AM là đường trung tuyến)
a) chứng minh tam giác ABM = tam giác ACM và AM là tia phân giác góc A
b) từ M vẽ ME vuông góc với AB tại E; MF vuông góc với AC tại F, chứng minh tam giác MAE = tam giác MAF và tam giác MEF cân
c) trên tia đối của tia MA lấy điểm H sao cho MA=MH, gọi M là trung điểm (H,y là giao điểm của CB và AN) chứng minh BC bằng 6 lần MI
cần gấp ạ!!
Cho tam giác ABC cân tại A có AM là đường trung tuyến a, Chứng minh △ABM = △ACM b, Từ M kẻ MH ⊥ AB ( H ∈ AB ) , kẻ MK ⊥ AC ( K ∈ AC) . Chứng minh MH = MK
cute quá ước gì có 1con nhỉ đúng không Nguyễn Lê Bảo Trúc
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A có AM là phân giác của góc BAC. Chứng minh tam giác ABM = tam giác ACM
Xét tam giác ABM và tam giác ACM
\(AB=AC\) ( \(\Delta\) ABC cân tại A )
\(\widehat{BAM}=\widehat{CAM}\) ( AM là p.giác góc BAC )
AM chung
=> \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC cân tại A với đường trung tuyến AM.
a) Chứng minh tam giác ABM=tam giác ACM.
b) Biết AB= 5 cm, BC=6 cm. Gọi G là trọng tâm của tam giác ABC, tính độ dài đoạn thẳng MG và so sánh góc ABG với góc GAC.
a,XétΔABM và ΔACM có :
^AMB=^AMC(=90o)
AB=AC(GT)
AM :cạnh chung(gt)
Suy ra:ΔABM= ΔACM (ch-cgv)
=>MB=MC( 2 cạnh tương ứng)
b,Ta có MB=BC2 =242 = 12
Δ AMB vuông tại M có :
AM2+BM2=AB2 ( đl Pytago)
=>AM2=AB2−BM2
= 202−122
= 162
=>AM=16
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại a đường vuông góc với 2 cạnh bên tại b và c cắt nhau tại m Chứng minh tam giác ABM = tam giác ACM Chứng minh AM là phân giác của góc BAC
a) Xét ΔABM vuông tại B và ΔACM vuông tại M có
AM chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABM=ΔACM(cạnh huyền-cạnh góc vuông)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A , M là trung điểm của cạnh BC , chứng minh rằng :
a) AM là đường trung tuyến của tam giác ABC
b) AM là đường phân giác góc A của tam giác đó
c) AM là đường trung trực của tam giác ABM
SOS mn cứu em!
a: M là trung điểm của BC
=>AM là đường trung tuyến của ΔABC
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
c: Sửa đề; tam giác ABC
AB=AC
BM=CM
=>AM là trung trực của BC
Đúng 0
Bình luận (0)
Tam giác ABC cân tại A. M là trung điểm cạnh BC
a ) Chứng minh tam giác ABM = tam giác ACM
b ) Đường thẳng M song song với AC cắt AB tại E. Chứng minh tam giác EAM cân
c ) I là trung điểm AC. Chứng minh BI, AM, CE đồng quy
Tam giác ABC cân tại A. M là trung điểm cạnh BC
a ) Chứng minh tam giác ABM = tam giác ACM
b ) Đường thẳng M song song với AC cắt AB tại E. Chứng minh tam giác EAM cân
c ) I là trung điểm AC. Chứng minh BI, AM, CE đồng quy
Cho tam giác ABC cân tại A có M là trung điểm của cạnh BC. Chứng minh rằng tam giác ABM = tam giác ACM
vì tam giác ABC cân-> AB=AC
do M là trung điểm của BC-> MB=MC
xét tam giác ABM và tam giác ACM có:
AB=AC(cmt)
BM=MC(cmt)
cạnh AM chung
->tam giác ABM=tam giác ACM(c.c.c)
Đúng 1
Bình luận (0)
Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (\(\Delta ABC\) cân)
\(\widehat{ABM}=\widehat{ACM}\)(\(\Delta ABC\) cân)
BM = CM (trung điểm M)
\(\Rightarrow\Delta ABM=\Delta ACM\)
Đúng 1
Bình luận (0)
Đây bạn ơi. Thật ra còn nhiều cách nữa nhưng mk mới chỉ liệt kê ra một số cách chi bạn tham khảo thôi

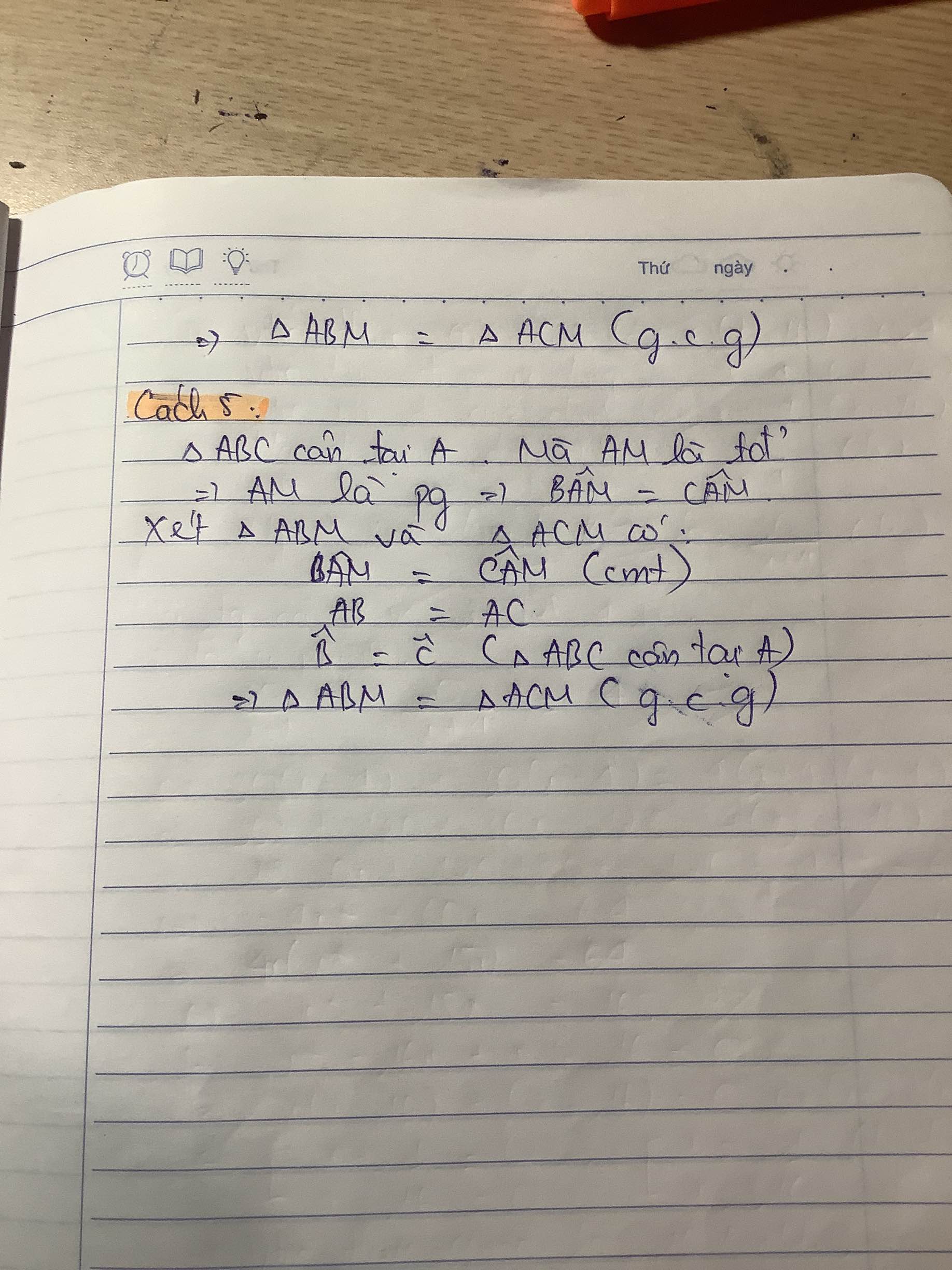
Đúng 1
Bình luận (0)
Xem thêm câu trả lời