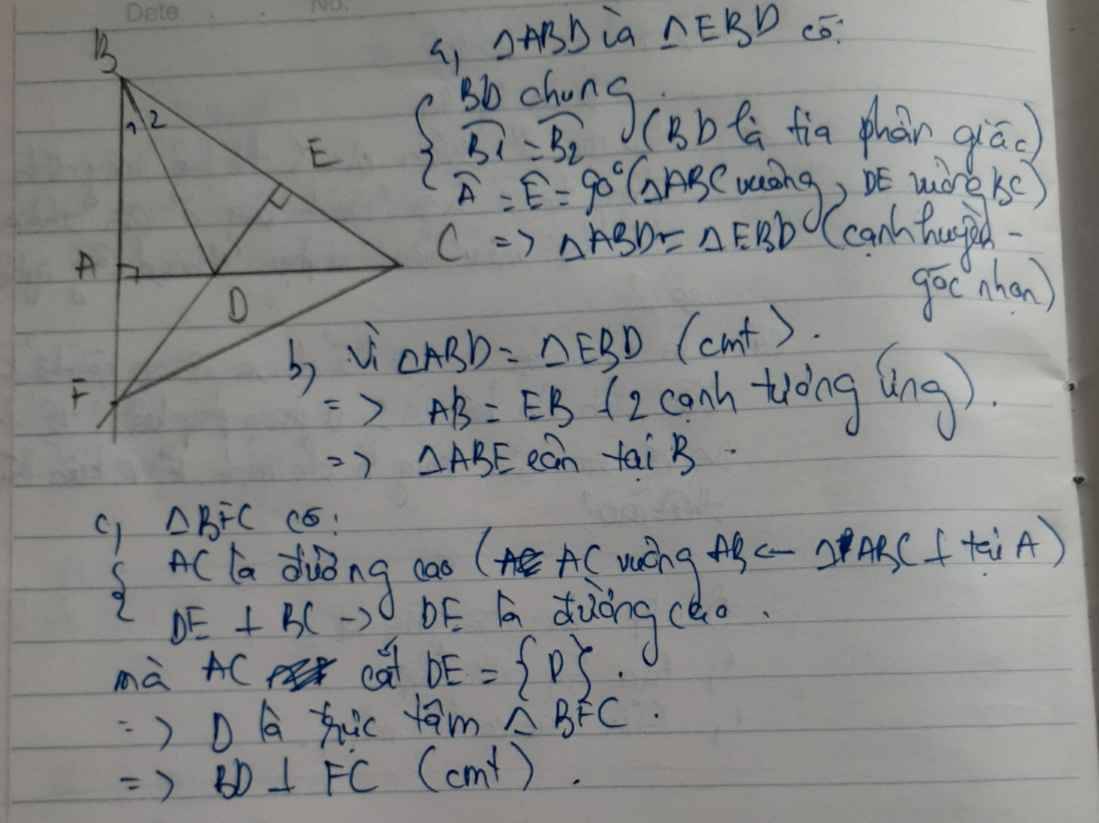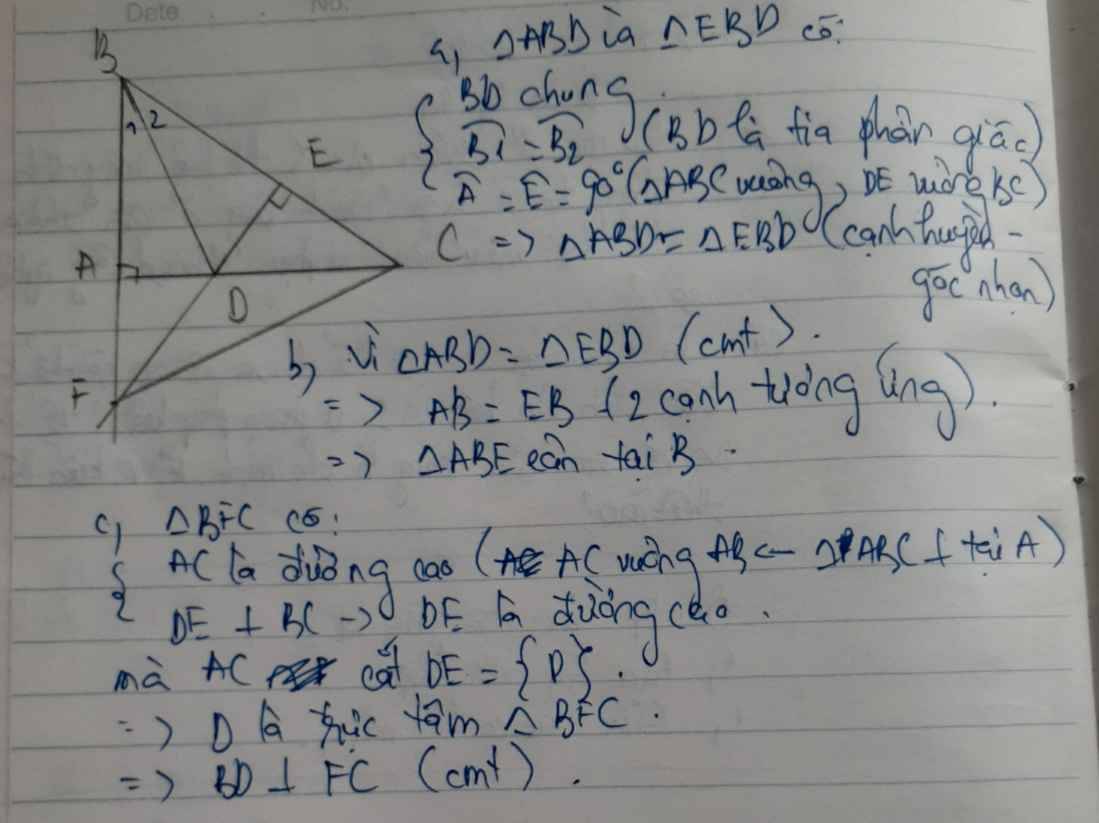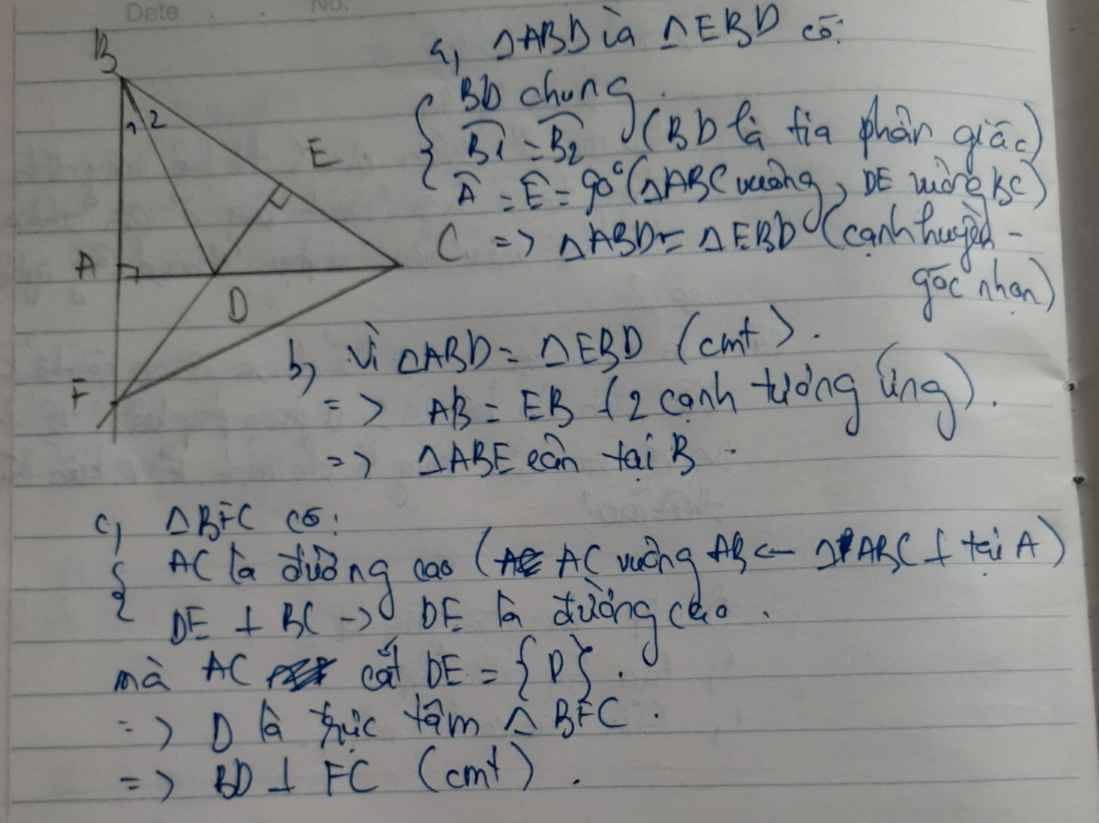abc vuông tại tại a phân giác của góc b cắt ac tại d từ d kẻ dh vuông góc với bc tại e a chứng minh tam giác abd = tam giác ebd b tam giác bae là tam giác gì vì sao c chứng minh rằng ae vuông góc với bd

Những câu hỏi liên quan
abc vuông tại tại a phân giác của góc b cắt ac tại d từ d kẻ dh vuông góc với bc tại e a chứng minh tam giác abd = tam giác ebd b tam giác bae là tam giác gì vì sao c chứng minh rằng ae vuông góc với bd
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔBAD=ΔBED
b: ta có: ΔBAD=ΔBED
nên BA=BE
hay ΔBAE cân tại B
c: Ta có: BA=BE
DA=DE
Do đó: BD là đường trung trực của AE
hay BD⊥AE
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC). Kẻ tia phân giác của góc ABC cắt đoạn AC tại D. Từ D kẻ dường thẳng vuông góc với BC cắt BC tại E. Tia BA cắt tia ED tại F.
a) Chứng minh tam giác ABD = tam giác EBD
b) Tam giác ABE là tam giác gì? Vì sao?
c) Chứng minh rằng BD vuông góc với CF
nhanh lên với ạ
Cho tam giác ABC vuông tại A . Tia phân giác của góc B cắt tại AC tại D. Từ D kẻ DH vuông góc với BC tại H.
a) Cho BC = 15cm , AB = 9cm . Tính AC.
b) Chứng minh tam giác ABD = tam giác HBD.
c) Tam giác ABH là tam giác gì?Vì sao?
d) Chứng minh : DC >DA.
cho tam giác abc vuông tại a có góc b bằng 60 độ, vẽ bd cắt ac tại d ,kẻ de vuông góc với bc tại e câu a chứng minh tam giác abd bằng tam giác ebd câu b tam giác abe là tam giác gì vì sao câu c tính chiều dài của cạnh bc
Cho tam giác ABC vuông tại A và AB <AC. Tia phân giác của góc ABC cắt cạnh AC tại D. Kẻ DE vuông góc với BC (điểm E thuộc BC).
a) Chứng minh rằng: Hai tam giác ABD và EBD bằng nhau;
b) Giải thích vì sao tam giác ADE là tam giác cân?
c) Chứng minh: 2.AD>AE;
d) Tia ED cắt tia BA tại F. Chứng minh: BD vuông góc với CF
a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
Đúng 2
Bình luận (0)
c) vì theo ý b) ADE là tam giác cân tại D nên theo py-ta-go AD+DE=AE
Nên AE>AD
(sai đầu bài rồi)
Đúng 1
Bình luận (0)
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB= 3cm, AC= 4cm. Phân giác của góc B cắt AC tại D. Kẻ DE vuông góc BC tại E a. Tính BC b. Chứng minh tam giác ABD= tam giác EBD c. So sánh BD với BC+CD từ đó chứng minh BD+DA < BC+AC
Cho tam giác ABC vuông tại A có góc C bằng 30°,tia phân giác của góc B cắt AC tại D,kẻ DE vuông góc BC tại E. a) Chứng minh ∆ABD=∆EBD b)Chứng minh tam giác ABE là tam giác đều. c)Chứng minh BD=DC GIÚP MÌNH VỚI Ạ
a) Xét ∆ABD và ∆EBD ta có :
BD chung
góc BAD = góc BED ( = 90 độ)
góc ABD = góc EBD ( gt)
=> ∆ABD=∆EBD ( ch-gn)
b) Xét tam giác vuông ABC ta có :
Góc A = 90 độ, góc C = 30 độ
Mà góc A + góc C + góc B = 180 độ
=> góc B = 180 - 90 - 30 = 60 độ (1)
Xét tam giác ABE ta có :
BA = BE ( vì ∆ABD=∆EBD) => tam giác ABE cân tại B
Mà góc B = 60 độ => Tam giác ABE là tam giác đều ( trong tam giác cân, một góc = 60 độ thì tam giác đó là tam giác đều )
Đúng 5
Bình luận (0)
a) Xét `∆ABD` và `∆EBD` ta có :
`BD` chung
`hat (BAD) = hat (BED) ( = 90^o)`
`hat(ABD) = hat (EBD)`
`=> ∆ABD=∆EBD ( ch-gn)`
b) Xét tam giác vuông `ABC` ta có :
`Hat A = 90 độ, hatC = 30 độ`
Mà `hat (A) + hat (C) + hat (B) = 180^o`
`=> hat(B) = 180 - 90 - 30 = 60 độ (1)`
Xét tam giác ABE ta có :
`BA = BE ( vì ∆ABD=∆EBD) =>` ` triangle ABE `cân tại B
Mà `hat(B)= 60 độ => triangle ABC` là tam giác đều
Đúng 3
Bình luận (0)
a) Xét ∆ABD và ∆EBD ta có :
BD chung
góc BAD = góc BED ( = 90 độ)
góc ABD = góc EBD ( gt)
=> ∆ABD=∆EBD ( ch-gn)
b) Xét tam giác vuông ABC ta có :
Góc A = 90 độ, góc C = 30 độ
Mà góc A + góc C + góc B = 180 độ
=> góc B = 180 - 90 - 30 = 60 độ (1)
Xét tam giác ABE ta có :
BA = BE ( vì ∆ABD=∆EBD) => tam giác ABE cân tại B
Mà góc B = 60 độ => Tam giác ABE là tam giác đều ( trong tam giác cân, một góc = 60 độ thì tam giác đó là tam giác đều )
Đúng 1
Bình luận (3)
Bài 1: Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BEBA. Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D.a) Tính độ dìa AC khi AB 9cm, BC 15cmb) Chứng minh: Tam giác ABDtam giác EBDc) Gọi H là giao điểm của đường thẳng AB và đường thẳng d. Chứng minh tam giác HBC când) Chứng minh: ADDCBài 2: Cho tam giác ABC vuông tại A có AB 12cm, AC 16cm.Kẻ BF là đường trung tuyến của tam giác ABC. Từ điểm C kẻ đường thẳng vuông góc với AC cắt đường trung tuyến BF tại Da) Tính độ dà...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA. Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D.
a) Tính độ dìa AC khi AB= 9cm, BC= 15cm
b) Chứng minh: Tam giác ABD=tam giác EBD
c) Gọi H là giao điểm của đường thẳng AB và đường thẳng d. Chứng minh tam giác HBC cân
d) Chứng minh: AD<DC
Bài 2: Cho tam giác ABC vuông tại A có AB= 12cm, AC= 16cm.Kẻ BF là đường trung tuyến của tam giác ABC. Từ điểm C kẻ đường thẳng vuông góc với AC cắt đường trung tuyến BF tại D
a) Tính độ dài BC?
b) Chứng minh rằng: Tam giác ABF=tam giác CDF
c) Chứng minh: BF<(AB+BC):2
Bài 3: Cho tam giacsABC vuông tại A; tia phân giác của góc B cắt AC tại D. Kẻ DH vuông góc với BC\(\left(H\in BC\right)\). Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 9cm, AC= 12cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh: Tam giác KDC cân
d) Chứng minh: AB+AC>BD+DC
Bài 4: Cho tam giác ABC vuông tại A. Trên tia BC lấy điểm H sao cho BH=BA. Tia phân giác của góc B cắt AC tại D. Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 3cm, AC= 4cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh \(Dh\perp BC\)
d) So sánh DH với DK
4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.
Đúng 0
Bình luận (0)
#)Góp ý :
Giải thì vẫn giải đc, chỉ tại dài quá, người nhìn thấy dài thì chẳng ai muốn giải đâu, vì lười, mak mún kiếm P nhanh mà, là mình thì vẫn giải đc nhưng sẽ mất tg đó, chắc 15-30p :v
Đúng 0
Bình luận (0)
Bài 1: a, áp dụng định lí py-ta-go vào t.giác vuông ta có:
\(BC^2=AC^2+AB^2\)
=> \(AC^2=BC^2-AB^2\)
=> \(AC^2\)=225-81=144
=>AC=12 (cm)
vậy AC=12 cm
b, xét 2 tam giác vuông ABD và EBD có:
BD cạnh chung
BA=BE(gt)
=> \(\Delta ABD=\Delta EBD\)(cạnh huyền-cạnh góc vuông)
c, ta có: \(\Delta ADH=\Delta EDC\)(cạnh góc vuông-góc nhọn)
=> AH=EC(2 cạnh tương ứng)
Mà AB=EB(câu b) => HB=CB
=> \(\Delta HBC\)cân tại B
d, trong tam giác vuông ADH có: AD<DH(vì cạnh huyền lớn hơn cạnh góc vuông) mà DH=DC=> DC>AD hay AD<DC đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC vuông tại A . Tia phân giác của góc B cắt AC tại D . Kẻ DE vuông góc với BC tại E . 1, chứng minh : tam giác ABD = tam giác EBD . 2, chứng minh : tam giác ABE là tam giác đều
TÔI LÀ THẦY GIÁO DẠY MÔN VĂN VÀ TOÁN. SAO KO VIẾT CHỦ NGỮ VÀO, CÓ THÍCH TÔI TRẢ LỜI KO?
Đúng 0
Bình luận (0)