Bổ sung vế còn lại để tạo thành hằng đẳng thức đúng:
(y-5).(y2+5y+25)
Những câu hỏi liên quan
bài 1: bổ sung các hạng tử còn thiếu trong hằng đẳng thức
y3- +12yz2- = (y - 2z)3
2: Viết lại các đa thức thành vế kia hằng đẳng thức:
a, 4x^(4)-4x^(2)+16
b, (x+2y)^(2).
c, 36+x^(2)-12xy
d, (x+5y)^(2).
e, 4x^(2)-12x+9
f,(x-2y)^(2).
\(4x^4-4x^2+1=\left(2x^2-1\right)^2\)
\(\left(x+2y\right)^2=x^2+4xy+4y^2\)
\(36-12x+x^2=\left(6-x\right)^2\)
\(\left(x+5y\right)^2=x^2+10xy+25y^2\)
\(4x^2-12x+9=\left(2x-3\right)^2\)
\(\left(x-2y\right)^2=x^2-4xy+4y^2\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử ( bằng kĩ thuật bổ sung hằng đẳng thức ):
c.x^2 - 7x +12
d.x^2 + 7x +12
c ) \(x^2-7x+12\)
\(=\left(x^2-3x\right)-\left(4x-12\right)\)
\(=x\left(x-3\right)-4\left(x-3\right)\)
\(=\left(x-4\right)\left(x-3\right)\)
d ) \(x^2+7x+12\)
\(=\left(x^2+3x\right)+\left(4x+12\right)\)
\(=x\left(x+3\right)+4\left(x+3\right)\)
\(=\left(x+4\right)\left(x+3\right)\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử ( bằng kĩ thuật bổ sung hằng đẳng thức ):
a.x^2 - 5x + 6
b.x^2 + 5x + 6
a ) \(x^2-5x+6\)
\(=\left(x^2-2x\right)-\left(3x-6\right)\)
\(=x\left(x-2\right)-3\left(x-2\right)\)
\(=\left(x-2\right)\left(x-3\right)\)
b )\(x^2+5x+6\)
\(=\left(x^2+2x\right)+\left(3x+6\right)\)
\(=x\left(x+2\right)+3\left(x+2\right)\)
\(=\left(x+2\right)\left(x+3\right)\)
Đúng 0
Bình luận (0)
a.x^2 - 5x + 6
=x2-2x-3x+6
=x(x-2)-3(x-2)
=(x-3)(x-2)
b.x^2 + 5x + 6
=x2+3x+2x+6
=x(x+3)+2(x+3)
=(x+2)(x+3)
Đúng 0
Bình luận (0)
Phân tích thành nhân tử xử dụng phương pháp bổ sung hằng đẳng thức
x2 - x + 20
6x^2+7x-3(bổ sung hằng đẳng thức)
Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu):
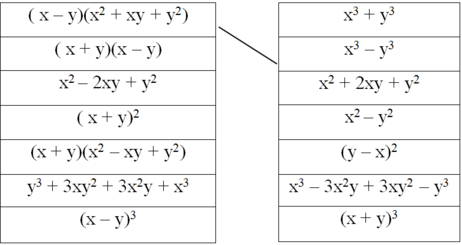
Viết lại đa thức thành vế kia hằng đẳng thức
a. (2x - 3y)^2
b (3\(\sqrt{x}\)- y)^2
( 2x - 3y )2 = 4x2 - 12xy + 9y2
( 3√x - y )2 = 9x - 6y√x + y2 ( x ≥ 0 )
viết vế còn lại của hằng đẳng thức
4x^2-20xy^2+25Y^4
\(4x^2-20xy^2+25y^4=\left(2x\right)^2-2.2x.5y^2+\left(5y^2\right)^2=\left(2x-5y^2\right)^2\)
Áp dụng hằng đẳng thức: \(\left(A-B\right)^2=A^2-2AB+B^2\)
Đúng 0
Bình luận (0)
\(4x^2-20xy^2+25y^4\)
\(=\left(2x\right)^2-2\cdot2x\cdot5y^2+\left(5y\right)^2\)
\(=\left(2x-5y\right)^2\)
Đúng 0
Bình luận (0)
\(4x^2-20xy^2+25y^4\)
\(=\left(2x\right)^2-2.2.5.xy^2+\left(5y\right)^2\)
\(=\left(2x-5y\right)^2\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời