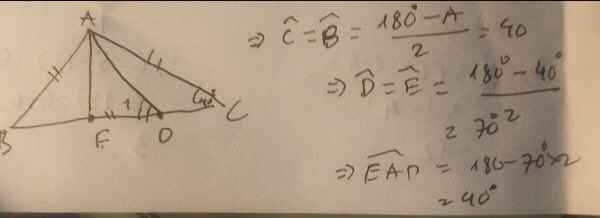Bài 6: Cho hình vẽ biết AB = AC = BC = BD = CE. Tính số đo góc DAE

Những câu hỏi liên quan
Cho hình vẽ, biết BD vuông góc với AC, AE vuông góc với AC, BC = 6, AB = x, CD = 3x, CE = 13,5. Tính x.
ta có: BD // AE ( cùng vuông với AC)
Áp dụng định lý talet, ta có:
\(\dfrac{BC}{BA}=\dfrac{CD}{DE}\)
<=>\(\dfrac{6}{x}=\dfrac{3x}{13,5-3x}\)
<=>6.(13,5-3x)=3x.x
<=>81-18x=3x^2
<=>\(3x^2+18x-81=0\)
<=> x=3(n)
x=-9(l)
Đúng 2
Bình luận (2)
Bài 1: Cho tam giác đều ABC, trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE=BC
a) CM tam giác ADE cân
b) Tính góc DAE
Bài 2: Cho tam giác ABC cân tại A, CE vuông góc với AB, lấy điểm M nằm giữa B và C, vẽ MI vuông góc với AC. (E thuộc AB, I thuộc AB, J thuộc AC). CM MI + MJ = CE
Cho tam giác ABC. Vẽ các đường phân giác BD và CE(D thuộc AC và E thuộc AB). Tính số đo của góc A biết BE + CD=BC
Cho tam giác ABC cân tại A có ∠A = 80 độ. Trên cạnh BC lấy điểm D và E sao cho BD
= AB, CE = AC. Tính số đo ∠DAE.
\(\Delta\)ABC cân tại A nên \(\widehat{B}=\widehat{C}\)
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(định lí)
mà \(\widehat{B}=\widehat{C}\)
=> \(\widehat{A}+2\widehat{B}=180^0\)
=> \(\widehat{A}=180^0-2\widehat{B}\)
=> \(180^0-2\widehat{B}=80^0\)
=> \(2\widehat{B}=100^0\)
=> \(\widehat{B}=50^0\)
Do đó \(\widehat{B}=\widehat{C}=50^0\)
Ta có : BD = BA => \(\Delta\)ABD cân tại B => \(\widehat{BAD}=\widehat{BDA}\)
\(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{B}}{2}=\frac{180^0-50^0}{2}=65^0\)
=> \(\widehat{BAD}=65^0\)
CE = CA => \(\Delta\)ACE cân tại C => \(\widehat{CAE}=\widehat{CEA}\)
Do đó \(\widehat{CAE}=\widehat{CEA}=\frac{180^0-\widehat{C}}{2}=\frac{180^0-50^0}{2}=65^0\)
=> \(\widehat{CAE}=65^0\)
Xét \(\Delta\)DAE theo định lí tổng ba góc trong 1\(\Delta\))
=> \(\widehat{BAD}+\widehat{CAE}+\widehat{DAE}=180^0\)
=> \(65^0+65^0+\widehat{DAE}=180^0\)
=> \(\widehat{DAE}=180^0-130^0=50^0\)
Vậy \(\widehat{DAE}=50^0\)
Góc DAE = 80 độ
Cho tam giác ABC cân tại A . lấy các điểm D , E thuộc BC sao cho BD = BA , CA = CE . tính số đo góc DAE , biết góc A bằng 80 độ .
chịu nha bn nhưng k mk nha Việt Nam
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Lấy các điểm D,E thuộc cạnh BC sao cho BD=BA và CA=CE. Tính số đo góc DAE biết góc A = 80 độ
đừng tích ai nhá, tôi về mình giải cho, giờ mik phải đi học thêm
Đúng 1
Bình luận (0)
xin lỗi bn mik ko học lớp 7
Chúc bn hok tốt
^_^
Bài 3 tam giác ABC cân tại A có A bằng 100 độ lấy các điểm D và E trên cạnh BC sao cho BD = BA, CE = CA tính số đo góc DAE
Cho tam giác ABC cân tại A có ∠A = 800. Trên cạnh BC lấy điểm D và E sao cho BD
= AB, CE = AC. Tính số đo ∠DAE.
Bài 4: Cho tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm.
a) Chứng tỏ tam giác ABC vuông.
b) Kẻ phân giác BD và CE (D thuộc AC, E thuộc AB), BD và CE cắt nhau tại I. Tính số đo góc IBC
Tự vẽ hình.
a) Ta có: \(AB^2+AC^2=8^2+6^2=100\); \(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\)
Theo định lý Pytago đảo \(\Rightarrow\Delta ABC\) vuông tại \(A\).
b) Xét tam giác \(IBC\). Theo định lý tổng 3 góc trong tam giác ta có
\(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\\ \Rightarrow\widehat{BIC}=180^0-\left(\widehat{IBC}+\widehat{ICB}\right)\\ \Rightarrow\widehat{BIC}=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)\\ \Rightarrow\widehat{BIC}=180^0-\dfrac{1}{2}\left(180^0-\widehat{A}\right)\\ \Rightarrow\overrightarrow{BIC}=180^0-\dfrac{1}{2}\left(180^0-90^0\right)=135^0\)
Đúng 2
Bình luận (1)