Mọi người giải giúp em câu này với ạ em cần ngay trong ngay mai ạ 

Những câu hỏi liên quan
Giải giúp em đề này với ạ! Em cần ngay trong 45’ nữa ạ! Cảm ơn mọi người nhiều!
Bạn cần bài nào ạ? Nếu bạn cần giúp tất cả thì bạn tách ra từng CH khác nhau nhé!
Đúng 0
Bình luận (0)
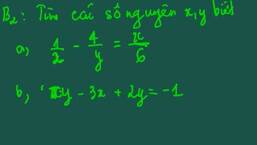
Mọi người ơi!! Mọi người giúp em với ạ. Em cần luôn ngay bây giờ. Em cảm ơn nhiều.
mọi người giúp em với ạ, e cần giải thích của câu này ạ

Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.
Đúng 0
Bình luận (0)
Tìm 1 cách chứng minh khác của định lí 2
Có ai biết không ạ! Giải bài tập này dùm em với, bài quan hệ giữa đường vuông góc và đường xiên, hình chiếu và đường xiên ạ!
Em cần lời giải ngay hôm nay ạ! Mong mọi người giúp đỡ!
bài này mk bt lm nhưng mk đag trog trạng thái mệt mỏi nên ngại lắm, để lúc nào rảnh mk giúp bn nhé!
Đúng 0
Bình luận (0)
Mọi người giúp em câu này với ạ, mai em thi rồi TvT
Đọc tiếp
Mọi người giúp em câu này với ạ, mai em thi rồi TvT
Mọi người giải giúp em bài này với ạ. Em cần gấp lắm ạ. Cảm ơn mọi người nhiều
vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )
Đúng 3
Bình luận (2)
em ơi chụp cả cái mạch điện a xem nào sao chụp nó bị mất r
Đúng 1
Bình luận (1)
 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ
a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)
Đúng 1
Bình luận (0)
Mọi người giải giúp em bài này với ạ, em đang cần gấp lắm ạ
Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
Đọc tiếp
 Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!




















