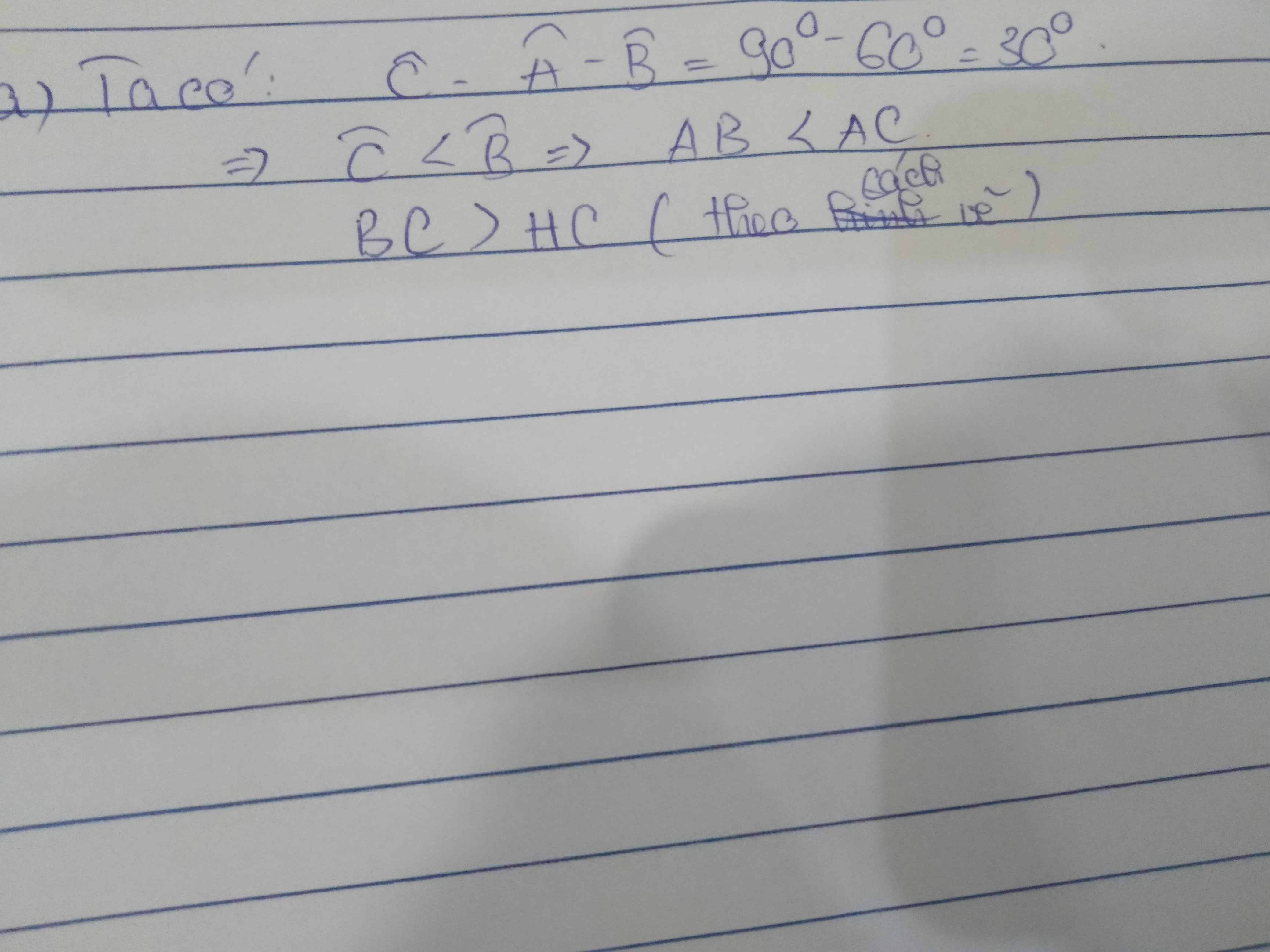Bài Cho tam giác ABC vuông tai A, góc B có só do bàng 60. va AH vuông góc vói BC tai H. a) So sánh AB và AC; BH và HC b) Láy diêm D thuso tin déi cua tia HA sao cho HD HA. Chúng minh ràng, hai tam giác AHC và DHC băng nhau. số do cua góc BDC

Những câu hỏi liên quan
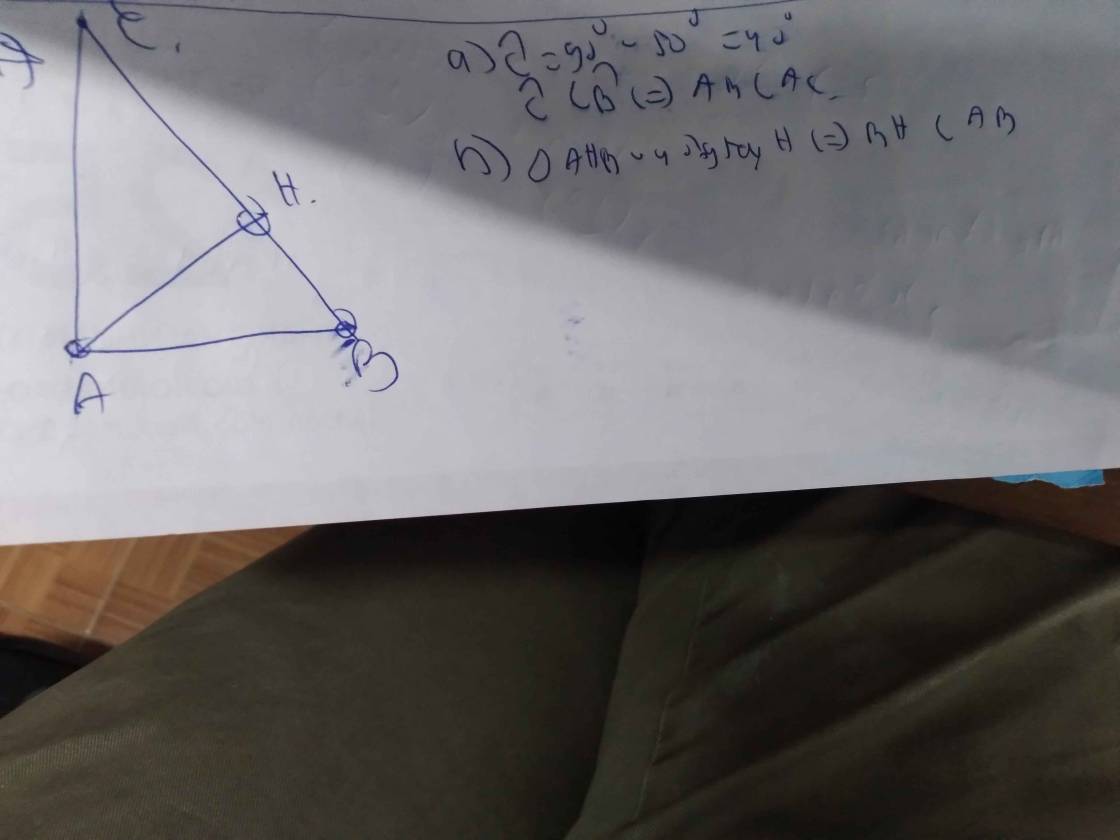
Cho tam giác ABC vuông tại A, góc B có số đo bằng 60⁰. Vẽ AH vuông góc với BC, (H ∈BC).
a) So sánh AB và AC; BH và HC
b) Lấy điểm D thuốc tía đối của tai HA sao cho HD = HA. Chứng minh rằng hai tam giác AHC và DHC bằng nhau
c) Tính số đó góc BDC
Cho tam giác ABC vuông tại A góc B=60 độ,Vẽ AH vuông góc với BC,(H thuộc BC)
a,So sánh AB và AC;BC và HC
cho tam giác ABC vuông tai A có ( AB < AC) tia Bx là phân giac của góc B cắt AC tai D, từ C vẽ đường vuông góc vói Bx tại E. gọi M là trung điểm của BC, qua D vẽ đường vuông goc với DM cắt AB tại K và CE tai H. chứng minh DH=DK
bài 6: Cho tam giác ABC vuông tại A, góc B có số đo bằng 60 độ. Vẽ AH vuông góc với BC,(H thuộc BC)
a) So sánh AB và AC; BH và HC
b) Lấy điểm D thuộc tia đối của tia HA sao cho HD=HA. Chứng minh rằng: tam giác AHC= tam giác DHC
c) Tính số đo của góc BDC
Các bạn vẽ hình và ghi giải thiết kết luận với ạ em xin cảm ơn
a: \(\widehat{C}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{C}< \widehat{B}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
Do đó: ΔAHC=ΔDHC
c: Xét ΔBAC và ΔBDC có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
Đúng 4
Bình luận (0)
bài 6: Cho tam giác ABC vuông tại A, góc B có số đo bằng 60 độ. Vẽ AH vuông góc với BC,(H thuộc BC)
a) So sánh AB và AC; BH và HC
b) Lấy điểm D thuộc tia đối của tia HA sao cho HD=HA. Chứng minh rằng: tam giác AHC= tam giác DHC
c) Tính số đo của góc BDC
a: \(\widehat{C}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{C}< \widehat{B}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
Do đó: ΔAHC=ΔDHC
c: Xét ΔBAC và ΔBDC có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B=50° a,so sánh AB và AC b,kẻ Ah vuông góc với BC tại h so sánh Bh và AB khi BC=2AB
1, cho tam giác ABC có vuông góc tại A , vẽ AH vuông góc BC tại H , biết AB=12cm, AC= 9cm . tính AH,BH,CH
2, cho tam giác ABC vuông tai AB=x , AC= x+1 , BC = x +2 . hãy tìm x
Cho tam giác ABC vuông tại A .Tia phân giác của góc ABC cắt AC tai D. Từ D kẻ đường thẳng DH vuông goc với BC tai H và DH cắt AB tai K
A, cmr .AD=DH
B, so sánh độ dai AD và DC
C, cm tam giác KBC là tam giác cân
Bài 1. Cho tam giác ABC có AB= 8cm, AC=6cm, BC= 10 cm
a. Chứng minh tam giác ABC vuông
b. Vẽ AH vuông góc vs BC tại H. So sánh HB và AB. So sánh HC và AC
c. So sánh HB và HC