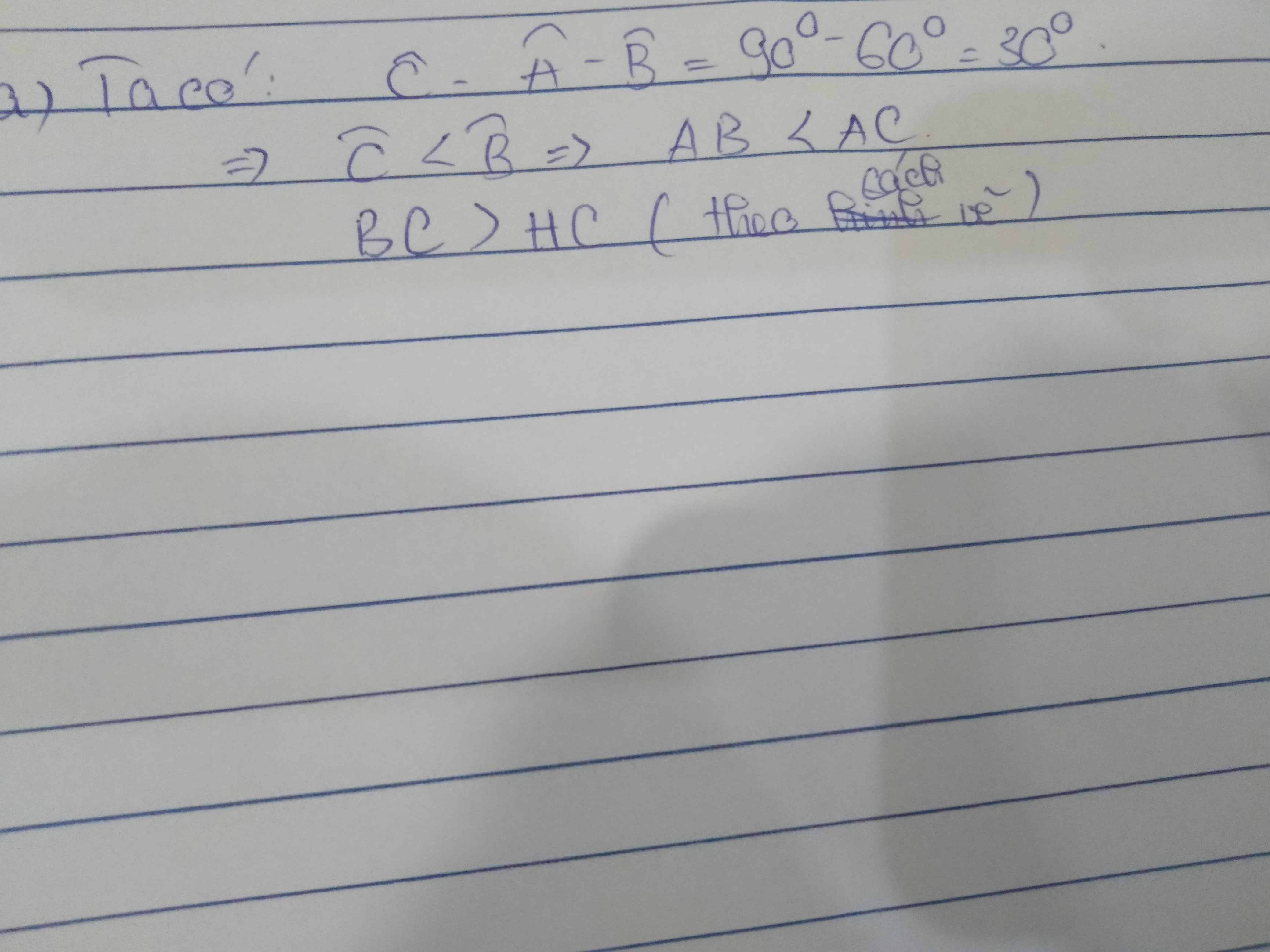Ôn tập Tam giác
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A biết AB = 9 cm AC bằng 12 cm Kẻ BD là tia phân giác của góc B( d thuộc AC) kẻ dh vuông góc với BC( H thuộc BC). Trên tia đối của tia ab lấy điểm K sao cho a k = HC a) Chứng minh tam giác ABD= tam giác HBD b) So sánh DA và DC c) Chứng minh ba điểm k,d,hthẳng hàng
Cho tam giác ABC có góc A = 90 độ. Kẻ AH vuông góc với BC (H thuộc BC)
a) Chứng minh góc BAH = góc ACB.
b) Tia phân giác góc BAH và tia phân giác góc ACB cắt nhau tại I. Tính góc AIC
c) Cho AC > AB Trên cạnh AC lấy điểm M sao cho CM= AB. So sánh CM và BH.
Cho tam giác ABC vuông tại A và góc B bằng 60 độ phân giác góc B cắt cạnh AC tại D kẻ đường vuông góc để e đến BC E thuộc BC a chứng minh ba = be,da =de b chứng minh tam giác bdc là tam giác cân c so sánh độ dài de và bc
CHO TAM GIÁC ABC VUÔNG TẠI A CÓ GÓC C=30 . KẺ AH VUÔNG GÓC BC. TRÊN ĐOẠN THẲNG HC LẤY D SAO CHO HD=HB. E LÀ CHÂN ĐƯỜNG VUÔNG GÓC KẺ TỪ C ĐẾN AD
. CHỨNG MINH
A, , AB=AD
B, TAM GIÁC ABD ĐỀU
C, SO SÁNH AH VÀ CE
D, BIẾT AB=5CM. TÍNH ĐỘ DÀI AH VÀ BC
Cho tam giác ABC cân tại A,AB=5cm,BC=8cm.kẻAH vuông góc với BC
a)cmr: HB=HC
b)tính AH
c)Vẽ HM vuông góc vơi AB,HN vuông góc với AC. Cm tam giác AMN là tam giáccaan
d) cmr : MN//BC
Xem chi tiết
Cho tam giác ABC cân tại A. Kẻ AH vuông góc BC (H thuộc BC).
a/ Chứng minh Tam giác AHB = Tam giác AHC. Từ đó suy ra HB = HC
b/ Biết AH = 8 cm, BC = 12 cm. Tính độ dài AC.
c/ Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh Tam giác HDE cân.
Cho ∆ABC vuông tại A có AB=9cm, AC=12cm A. Tính độ dài cạnh BC và so sánh các góc của ∆ABC B. Tia phân giác của góc ABC cắt AC tại D. Vẽ DH vuông góc BC(H thuộc BC). Chứng minh AD=HD C. Gọi E là giao điểm của 2 đường thẳng HD và BA. Kéo dài BD cắt tại T. CM: BI vuông góc EC
Cho tam giác ABC cân tại A (góc A nhọn). Vẽ đường phân giác của góc BAC cắt BC tại H:a) Chứng minh HBHC VÀ AH vuông góc BC.b) Với AB30 cm, BC 36 cm.Tính độ dài AH.c) Vể đường trung tuyến BM của tam giác ABC cắt AH tại G.Tính độ dài AG và BM. A B C H G M 1 2
Đọc tiếp
Cho tam giác ABC cân tại A (góc A nhọn). Vẽ đường phân giác của góc BAC cắt BC tại H:
a) Chứng minh HB=HC VÀ AH vuông góc BC.
b) Với AB=30 cm, BC= 36 cm.Tính độ dài AH.
c) Vể đường trung tuyến BM của tam giác ABC cắt AH tại G.Tính độ dài AG và BM.
Cho tam giác ABC vuông tại A ( AB<AC) tia phân giác của góc B cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE=BA. Vẽ AH vuông góc với BC tại H. Chứng minh rằng:
a) tam giác ABD= tam giác EBD và AD=ED
b) AH song song với BE