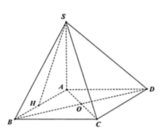
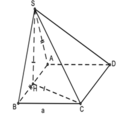
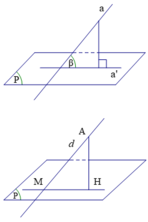
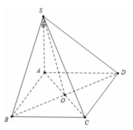
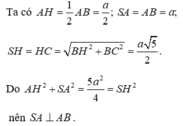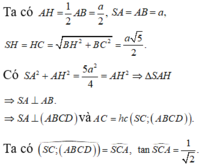Cho hình chóp S.ABCD có đáy ABCDlà hình vuông cạnh a ,( SAB ) vuông góc ( ABCD ) , H là trung điểm của AB ,SH=HC ,SA=AB . Tính góc giữa đường thẳng SC và mặt phẳng (ABCD)

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH HC, SA AB. Gọi
α
là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính giá trị của
tan
α
.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH = HC, SA = AB. Gọi α là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính giá trị của tan α .
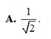
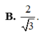
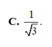

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH HC, SA AB. Gọi
α
là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính giá trị của
tan
α
A.
1
2
B.
2
3
C.
1
3
D.
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH = HC, SA = AB. Gọi α là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính giá trị của tan α
A. 1 2
B. 2 3
C. 1 3
D. 2
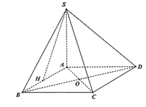
Ta có
A H = 1 2 A B = a 2 ; S A = A B = a S H = H C = B H 2 + B C 2 = a 5 2
Do A H 2 + S A 2 = 5 a 2 4 = S H 2 nên S A ⊥ A B
Do đó S A ⊥ A B C D nên S C , A B C D ^ = S C A ^
Trong tam giác vuông SAC có tan α = tan S C A ^ = S A A C = 1 2
Đáp án A
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH HC,SA AB. Gọi
α
là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị chính xác của tan
α
là? A.
1
2
B.
2
3
C....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH = HC,SA = AB. Gọi α là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị chính xác của tan α là?
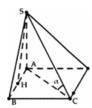
A. 1 2
B. 2 3
C. 1 3
D. 2
Đáp án A
Hướng dẫn giải: Ta có:
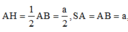
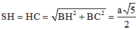
Có A H 2 + S A 2 = 5 a 2 4 = S H 2 ⇒ ∆ S A H vuông tại A
Do đó mà S A ⊥ ( A B C D ) nên
![]()
(Mặt phẳng (SAB) vuông góc với đáy (ABCD))
Trong tam giác vuông SAC, có
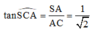
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, (SAB)
⊥
(ABCD). H là trung điểm của AB, SH HC, SA AB. Gọi
α
là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của
tan
α
là:
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, (SAB) ⊥ (ABCD). H là trung điểm của AB, SH = HC, SA = AB. Gọi α là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của tan α là:
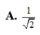
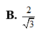
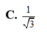
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a,
S
A
B
⊥
A
B
C
D
. H là trung điểm của AB, SHHC,SASB Gọi là góc giữa đường thẳng SC và mặt phẳng (ABCD) Giá trị của
tan
α
là: A.
1
2
B.
2
3
C.
1...
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, S A B ⊥ A B C D . H là trung điểm của AB, SH=HC,SA=SB Gọi là góc giữa đường thẳng SC và mặt phẳng (ABCD) Giá trị của tan α là:
A. 1 2
B. 2 3
C. 1 3
D. 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD) Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với Tính góc giữa đường thẳng SO và mặt phẳng (ABCD) A.
60
o
B.
69
,
3
o
C.
90
o
D.
45
o
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD) Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với 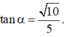 Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
A. 60 o
B. 69 , 3 o
C. 90 o
D. 45 o
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng đáy, SA = \(a\sqrt{2}\), góc giữa đường thẳng SC và mặt phẳng đáy bằng 45o. Gọi M là trung điểm của cạnh AB. Tính theo a khoảng cách h giữa hai đường thẳng DM và SB.
Help me!!!!
Gấp lắm ạ
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với
tan
α
10
5
. Tính góc giữa đường thẳng SO và mặt phẳng (ABCD). A.
60
°
B.
69
,
3
°
C.
90
°
D.
45
°
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng α với tan α = 10 5 . Tính góc giữa đường thẳng SO và mặt phẳng (ABCD).
A. 60 °
B. 69 , 3 °
C. 90 °
D. 45 °
Đáp án A
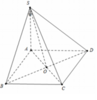
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy, SA AB a. Tính góc giữa đường thẳng SC và mặt phẳng . A. arcsin
1
4
B. arcsin
1
3
C. arcsin
1
3
D. arcsin
2
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy, SA = AB = a. Tính góc giữa đường thẳng SC và mặt phẳng .
A. arcsin 1 4
B. arcsin 1 3
C. arcsin 1 3
D. arcsin 2 3
Đáp án C
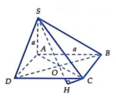
Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
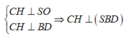
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có ![]()
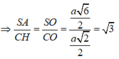
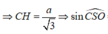
![]()
Đúng 0
Bình luận (0)