Cho đường tròn tâm O bán kính R, đường kính AB và dây CD vuông góc với AB(AC

Những câu hỏi liên quan
Cho đường tròn tâm O bán kính R,dây AB = R.căn 3 .Vẽ đường kính CD vuông góc AB(C thuộc cung AB lớn).Trên cung AC lấy M.Vẽ dây AN//CM.Tính MN
Cho đường tròn (O) đường kính AB. Vẽ dây CD không qua tâm vuông góc với AB tại I (A thuộc cung nhỏ CD) biết CD=16cm ; IA=6cm. Tính bán kính của (O;R)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔACB vuông tại C
ΔOCD cân tại O
mà OI là đường cao
nên I là trung điểm của CD
=>IC=ID=CD/2=8cm
Xét ΔCAB vuông tại C cso CI là đường cao
nên CI^2=IA*IB
=>8^2=6*IB
=>IB=64/6=32/3(cm)
AB=IB+IA=32/3+6=50/3(cm)
=>R=50/3:2=25/3(cm)
Đúng 0
Bình luận (0)
cho nửa đường tròn tâm O bán kính r , đường kính AB và dây cung CD . Vẽ AK vuông góc CD tại K , BL vuông góc CD tại L . CM : CK=DL
Cho nửa đường tròn tâm O, đường kính AB= 2r và 1 dây CD (C thuộc AD)
a) Hạ AP và BQ vuông góc với CD.c/m CP=DQ
b) Cho AC= r và góc COD =90 độ. Tính CD và CB theo r
c) Cho AP=48 cm, BQ=120cm, biết PQ =154 cm. Tính bán kính đường tròn
a: kẻ OH\(\perp\)CD tại H
Ta có: OH\(\perp\)CD
AP\(\perp\)CD
QB\(\perp\)CD
Do đó: OH//AP//QB
Xét hình thang ABQP(AP//QB) có
O là trung điểm của AB
OH//AP//BQ
Do đó: H là trung điểm của PQ
=>HP=HQ
Ta có: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
=>HC=HD
Ta có: HC+CP=HP
HD+DQ=HQ
mà HP=HQ và HC=HD
nên CP=DQ
b: Ta có: ΔOCD vuông tại O
=>\(OC^2+OD^2=CD^2\)
=>\(CD^2=R^2+R^2=2R^2\)
=>\(CD=R\sqrt{2}\)
Xét ΔOAC có OA=OC=AC=R
nên ΔOAC đều
=>\(\widehat{CAO}=60^0\)
=>\(\widehat{CAB}=60^0\)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C có \(sinCAB=\dfrac{CB}{AB}\)
=>\(\dfrac{CB}{2R}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(CB=R\sqrt{3}\)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R, dây BC khác đường kính, Hai tiếp tuyến của đường tròn (O;R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a) Chứng minh $AO bot BC.$
b) Cho biết $R 15, BC 24 (cm).$ Tính AB, OA.
c) Chứng minh BC là tia phân giác $widehat{ABH}.$
Em cần câu c thôi ạ.
Hình vẽ.
Đọc tiếp
Cho đường tròn tâm O bán kính R, dây BC khác đường kính, Hai tiếp tuyến của đường tròn (O;R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a) Chứng minh $AO \bot BC.$
b) Cho biết $R = 15, BC = 24 (cm).$ Tính AB, OA.
c) Chứng minh BC là tia phân giác $\widehat{ABH}.$
Em cần câu c thôi ạ.
Hình vẽ.
\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)
Đúng 3
Bình luận (2)
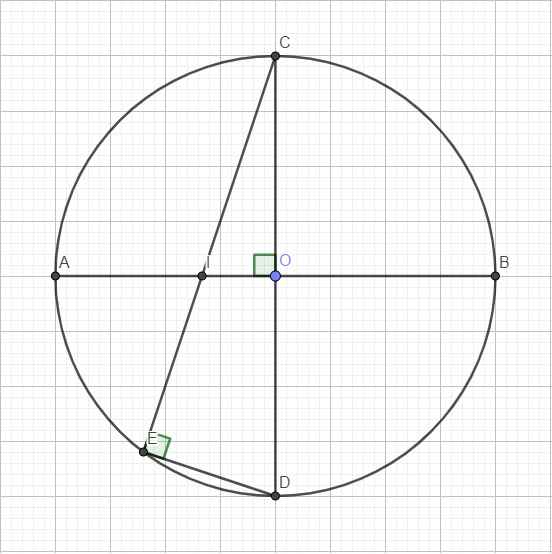
Cho đường tròn tâm O bán kính R, có hai đường kính AB và CD vuông góc với nhau.
Trên bán kính OA lấy điểm I sao cho AI=2/3 R
. Tia CI cắt đường tròn (O) tại điểm thứ hai E.
a) Chứng minh tam giác COI và tam giác CED đồng dạng
b) Tính độ dài dây CE.
b.
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)
Đúng 2
Bình luận (0)
a: Xét (O) có
ΔCED nội tiếp đường tròn
CD là đường kính
Do đó: ΔCED vuông tại E
Xét ΔCOI vuông tại O và ΔCED vuông tại E có
\(\widehat{ICO}\) chung
Do đó: ΔCOI\(\sim\)ΔCED
Đúng 2
Bình luận (0)
cho đường tròn tâm O bán kính R, trong đường tròn (O) lấy điểm P cách tâm O một khoảng bằng R/2. qua P kẻ hai dây AB và CD vuông góc với nhau(A,B,C,D là các điểm nằm trên đường tròn).tính tổng AB^2+CD^2 theo R
Jrouf8o7o98auoxur9hc9keuoa
Cho đường tròn tâm O bán kính R, dây AB không qua tâm O, I là trung điểm của AB. AB dài 16cm, bán kính R= 10 cm
a) Tính OI
b) OI cắt đường tròn O tại M . Tính AM
c) Kẻ đường kính MN của đường tròn tâm O, kẻ OK vuông góc với AN tại K. Tính AK
a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho đường tròn tâm O bán kính R . Hai dây AB và CD vuông góc với nhau . Chứng minh AC2 + BD2 = 4R2