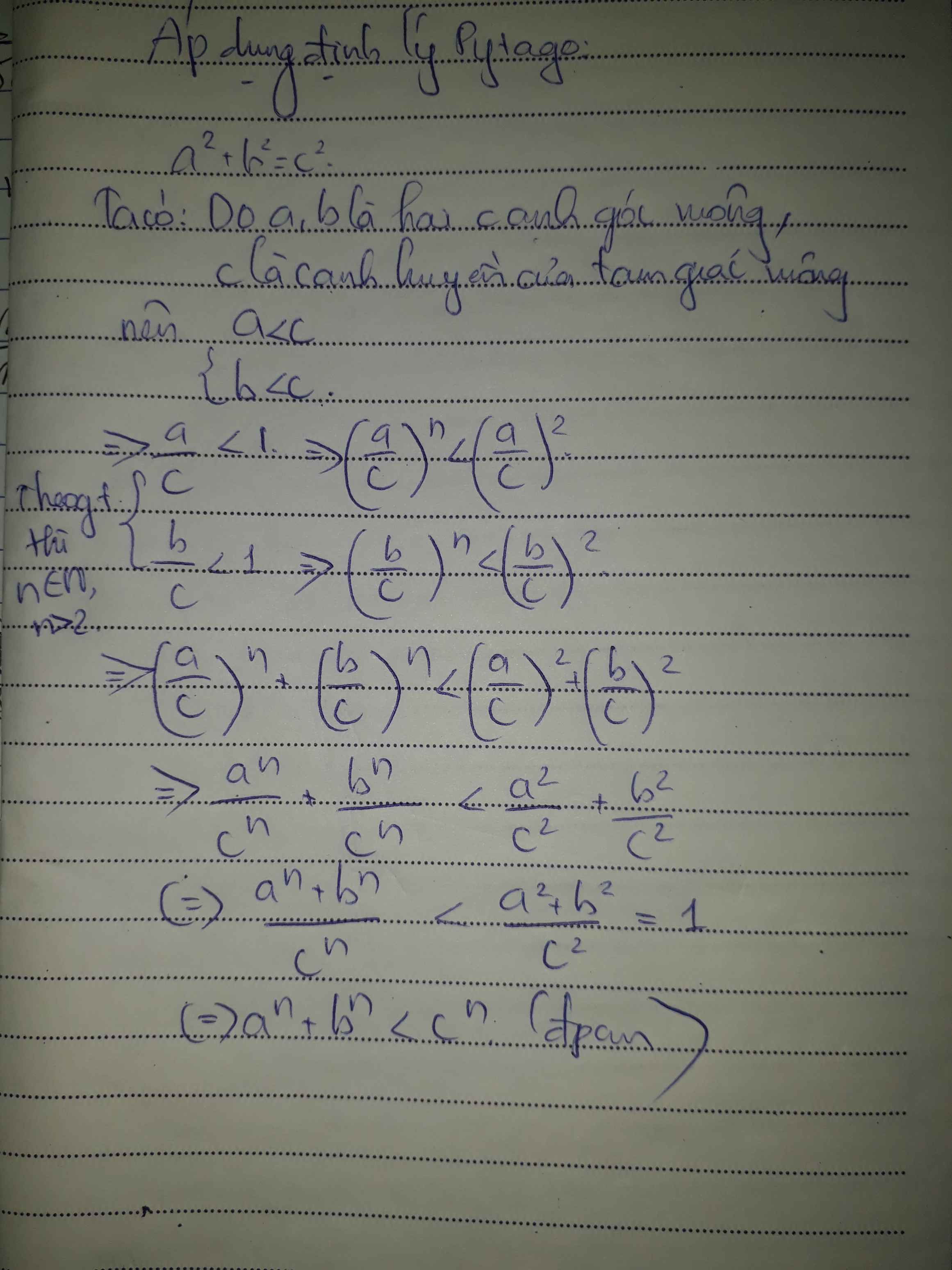cho tam giác vuông tại có a , b là 2 cạnh góc vuông c là cạnh huyền chứng minh \(c\ge\frac{a+b}{\sqrt{2}}\)

Những câu hỏi liên quan
cho tam giác vuông có hai cạnh góc vuông là a và b, c là cạnh huyền cm \(c\ge\frac{a+b}{\sqrt{2}}\)
lm nhanh dùm e nhoa mấy opaa
đây nhé bạn!
http://olm.vn/hoi-dap/question/596084.html
Đúng 0
Bình luận (0)
a,b,c là độ dài 3 cạnh tam giác
→a,b,c > 0
a2 + b2 > hoặc = 2ab
tương đương 2.( a2 +b2 ) > hoặc = ( a+b )2
mà a2 + b2 = c2 ( đl pytago )
→2.c2 > hoặc = ( a+b )2
tương đương căn 2.c> hoặc = a+b
tương đương c > hoặc = a+b trên căn 2
Đúng 0
Bình luận (0)
Gọi a, b là hai cạnh góc vuông, c là cạnh huyền của tam giác ABC vuông tại C. Chứng minh rằng với n ϵ N; n > 2 thì \(c^{n} > a^{n} + b^{n}\).
cho tam giác vuông ABC vuông tại A và M là trung điểm của BC, hãy chỉ ra cạnh huyền, cạnh góc vuông, trung tuyến ứng với cạnh huyền. A cho cạnh AB=9cm, AC=12cm. tính BC,MA, diện tích tam giác ABC,ABM? B cho góc B bằng 45 độ, tính góc C, chứng minh tam giác ABC vuông cân và AM vuông góc với bc. tính AM
Cho tam giác ABC vuông tại A, có 3 cạnh a, b, c ( a là cạnh huyền )
\(\left(1+\frac{a}{b}\right)\left(1+\frac{a}{c}\right)>=3+2\sqrt{2}\)
Tam giác vuông ABC h là đường cao thuộc cạnh huyền a và b,c là hai cạnh góc vuông
chứng minh rằng 1/b^2+1/c^2=1/h^2
chứng minh rằng (ab+bc+ca)/2 <c^2 với a,b là 2 cạnh góc vuông của tam giác ABC còn c là cạnh huyền
khó em chưa học
tick nha
 nguyen hoang phi hung
nguyen hoang phi hung
Đúng 0
Bình luận (0)
chứng minh rằng (ab+bc+ca)/2 <c^2 với a,b là 2 cạnh góc vuông của tam giác ABC còn c là cạnh huyền
do a,b là 3 cạnh của tam giác vuông mà c là cạnh huyền=>\(c^2=a^2+b^2\)
nhân 2 vế với 2 ta đc ab+bc+ca<=2c^2 (2)
<=>ab+bc+ca<=a^2+b^2+c^2
<=>a^2+b^2+c^2-ab-bc-ca>=0
<=>(a-b)^2+(b-c)^2+(c-a)^2>=0 (1)
(1)đúng =>2 đúng
Đúng 0
Bình luận (0)
1, Cho hình thang vuông ABCD có góc B góc C 90 độ. 2 đg chéo vuông góc với nhau tại H, biết AB 3.sqrt{5}; AH 3 cm. a/ Tính HB, HC, HD;b/ CMR: frac{1}{AB^2}-frac{1}{CD^2}frac{1}{HB^2}-frac{1}{HC^2}2, Đg trung tuyến ứng vs cạnh huyền của 1 tam giác vuông là 25cm. Tỉ số 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền là 16 : 9. Tính độ dài 2 cạnh góc vuông ?
Đọc tiếp
1, Cho hình thang vuông ABCD có góc B = góc C = 90 độ. 2 đg chéo vuông góc với nhau tại H, biết AB = 3.\(\sqrt{5}\); AH= 3 cm.
a/ Tính HB, HC, HD;
b/ CMR: \(\frac{1}{AB^2}-\frac{1}{CD^2}=\frac{1}{HB^2}-\frac{1}{HC^2}\)
2, Đg trung tuyến ứng vs cạnh huyền của 1 tam giác vuông là 25cm. Tỉ số 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền là 16 : 9. Tính độ dài 2 cạnh góc vuông ?
1, Áp dụng định lý Pytago. Chứng minh rằng nếu ta có a, b, c 0 sao cho a m2 + n2 ; b m2 - n2 ; c 2mn thì a, b, c là số đo 3 cạnh của tam giác vuông.2, Các ạnh góc vuông của một tam giác vuông có độ dài a, b và diện tích bằng S. Tính các góc của tam giác vuông đó biết (a + b)23, Chứng minh rằng nếu a, b, c là độ dài ba cạnh của 1 tam giác vuông (với a là độ dài cạnh huyền) thì các số x, y, z sau đây cũng là độ dài cạnh của tam giác vuông: x 9a + 4b +8c ; y 4a + b+ 4c ; z 8a + 4b + 7c
Đọc tiếp
1, Áp dụng định lý Pytago. Chứng minh rằng nếu ta có a, b, c > 0 sao cho a = m2 + n2 ; b = m2 - n2 ; c = 2mn thì a, b, c là số đo 3 cạnh của tam giác vuông.
2, Các ạnh góc vuông của một tam giác vuông có độ dài a, b và diện tích bằng S. Tính các góc của tam giác vuông đó biết (a + b)2
3, Chứng minh rằng nếu a, b, c là độ dài ba cạnh của 1 tam giác vuông (với a là độ dài cạnh huyền) thì các số x, y, z sau đây cũng là độ dài cạnh của tam giác vuông: x = 9a + 4b +8c ; y = 4a + b+ 4c ; z = 8a + 4b + 7c