cho hình lập phươnng ABCD.A'B'C'D'
tính góc giữa AC' và mặt phẳng (DA'C')
Cho hình lập phương ABCD.A'B'C'D'. Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C). Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C).
A. 60°
B. 135°
C. 150°
D. 90°
Đáp án A.
Vẽ DH ⊥ A'C
Ta có: ![]()
![]()
Vậy góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc B H D ^
Trong ∆ A'DC vuông tại D
![]()
Trong ∆ HBD có
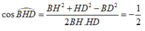
Suy ra góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc 60°.
Cho hình lập phương ABCD.A'B'C'D'. Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C). Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C).
A. 60 °
B. 135 °
C. 150 °
D. 90 °
Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
a) Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).
b) Tính đường chéo AC’ của hình lập phương đã cho.
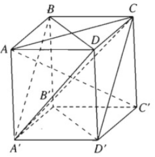
a) Ta có AB = AD = AA′ = a
và C ′ B = C ′ D = C ′ A ′ = a 2
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a
Vậy A C ′ 2 = A C 2 + C C ′ 2
⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .
Cho hình lập phương ABCD.A'B'C'D'. Gọi α là góc giữa AC' và mặt phẳng A ' B C D ' . Chọn khẳng định đúng trong các khẳng định sau?
A. α = 30 °
B. tan α = 2 3
C. α = 45 °
D. tan α = 2
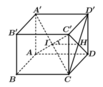
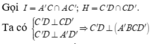
=> IH là hình chiếu vuông góc của IC' trên mặt phẳng A ' B C D '
Do đó ![]()
Trong tam giác vuông C'HI, có 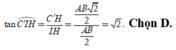
Cho hình lập phương ABCD.A’B’C’D’. Tính số đo góc giữa hai mặt phẳng (BA’C) và (DA’C). Tính số đo góc giữa hai mặt phẳng (BA’C) và (DA’C)
A. 60°
B. 135°
C. 150°
D. 90°
a) Cho hình lập phương ABCD. A'B'C'D' cạnh a. Chứng minh rằng đường thẳng AC' vuông góc với mặt phẳng (A'BD) và mặt phẳng (ACC'A') vuông góc với mặt phẳng (A'BD)
b) Tính đường chéo AC' của hình lập phương đã cho

b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)
Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa mặt phẳng (ABCD) và (ACC’A’).
A. 45 ο
B. 60 ο
C. 30 ∘
D. 90 ∘
Cho hình lập phương ABCD.A'B'C'D' . Gọi α là góc giữa đường thẳng AC’ với mặt phẳng (ABCD) . Mệnh đề nào dưới đây đúng?
A. 2 π 9 ≤ α ≤ π 4
B. π 4 < α < π 3
C. π 6 < α < 2 π 9
D. π 9 ≤ α ≤ π 6
Đáp án C
Ta có AC là hình chiếu vuông góc của AC' trên mặt phẳng (ABCD) .
Lại do C C ' ⊥ A B C D nên tam giác C'AC vuông tại C .
Suy ra A C ' , A B C D = A C ' , A C = C ' A C = α .
Ta có tan α = C C ' A C = 2 2 ⇒ π 6 < α < 2 π 9 .
Phân tích phương án nhiễu
Phương án A: Sai do HS tính được tan α 2 2 và cho rằng α = π 4 .
Phương án B: Sai do HS tính sai tan α = A C A C ' = 2 nên suy ra π 4 < α < π 3 .
Phương án D: Sai do HS tính sai tan α = C C ' A C ' = 3 3 nên suy ra α = π 6 .
Cho hình lập phương ABCD.A'B'C'D'. Gọi α là góc giữa đường thẳng AC’ với mặt phẳng (ABCd). Mệnh đề nào dưới đây đúng?
A . 2 π 9 ≤ α ≤ π 4
B . π 4 < α < π 3
C . π 6 < α < 2 π 9
D . π 9 ≤ α ≤ π 6
Đáp án C.

Ta có AC là hình chiếu vuông góc của A'C trên mặt phẳng (ABCD).
Lại do CC' ⊥ (ABCD) nên tam giác C'AC vuông tại C
Suy ra
![]()
Ta có
![]()
Phân tích phương án nhiễu
Phương án A: Sai do HS tính được tan α 2 2 và cho rằng α = π 4
Phương án B: Sai do HS tính sai
tan
α
=
A
C
A
C
'
=
2
nên suy ra ![]()
Phương án D: Sai do HS tính sai tan α = C C ' A C ' = 3 3 nên suy ra α = π 6