Đáp án A.
Vẽ DH ⊥ A'C
Ta có: ![]()
![]()
Vậy góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc B H D ^
Trong ∆ A'DC vuông tại D
![]()
Trong ∆ HBD có
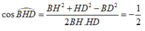
Suy ra góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc 60°.
Đáp án A.
Vẽ DH ⊥ A'C
Ta có: ![]()
![]()
Vậy góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc B H D ^
Trong ∆ A'DC vuông tại D
![]()
Trong ∆ HBD có
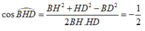
Suy ra góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc 60°.
Cho hình lập phương ABCD.A'B'C'D'
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Cho hình lập phương ABCD.A'B'C'D' Góc giữa hai mặt phẳng (A'B'CD) và (ABC'D') bằng
A. 30 °
B. 60 °
C. 45 °
D. 90 °
Cho hình lập phương ABCD.A'B'C'D Gọi E. F lần lượt là trung điểm các cạnh B'C', C'D' Côsin góc giữa hai mặt phẳng (AEF) và (ABCD) bằng
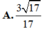
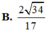
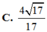
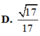
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với đáy sa=a . gọi M,N lần lượt là trung điểm của SB và SD . Tính số đo góc giữa hai mặt phẳng (AMN) và (ABCD)
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a và A B C ^ = 60 ° . Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 30 ° . Tính khoảng cách giữa hai đường thẳng SA, CD theo a ?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc BAD có số đo bằng 60 o . Hình chiếu của S lên mặt phẳng (ABCD) là trọng tâm tam giác ABC .Góc giữa (ABCD) và (SAB) bằng . Tính khoảng cách từ B đến mặt phẳng (SCD) .
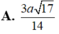
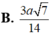
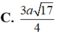
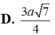
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc B A D ^ = 60 o và S A = S B = S D = a 3 2
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Cho hình chóp S.ABC có các mặt ABC và SBC là các tam giác đều và nằm trong hai mặt phẳng vuông góc với nhau. Số đo của góc giữa đường thẳng SA và (ABC) bằng
A. 45⁰.
B. 75⁰.
C. 60⁰.
D. 30⁰.
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BD′BD′ và mặt phẳng (ADD'A') bằng
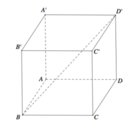
A. 3 3
B. 6 3
C. 2 2
D. 2 6