cho các số x1;x2;x3 thỏa mãn: x1 - 1/3 x2-2/2 = x3-3/1 và x1+x2+x3=30 . khi đó x1.x2-x2.x3 = ?

Những câu hỏi liên quan
Cho hàm số
y
x
3
+
2
m
−
2
x
2
−
5
x
+
1
. Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị
x
1
,
x
2
(
x
1...
Đọc tiếp
Cho hàm số y = x 3 + 2 m − 2 x 2 − 5 x + 1 . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 − x 2 = − 2 .
A. 7 2
B. ‒1
C. 1 2
D. 5
Đáp án C.
Ta có y ' = 3 x 2 + 4 m − 2 x − 5 ; y ' = 0 ⇔ 3 x 2 + 4 m − 2 x − 5 = 0 (*).
Phương trình (*) có a c < 0 nên luôn có hai nghiệm trái dấu .
Suy ra x 1 = − x 1 ; x 2 = x 2 .
Khi đó x 1 , x 2 là hai điểm cực trị của hàm số.
x 1 − x 2 = − 2 ⇔ − x 1 − x 2 = − 2 ⇔ x 1 + x 2 = 2 ⇔ − 4 m − 2 3 = 2 ⇔ m = 1 2
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
2
m
−
2
x
2
−
5
x
+
1
. Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị
x
1
,
x
2
(
x
1...
Đọc tiếp
Cho hàm số y = x 3 + 2 m − 2 x 2 − 5 x + 1 . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 − x 2 = − 2 .
A. 7 2
B. ‒1
C. 1 2
D. 5
cho x1,..x2016 thỏa mãn:1/x1^2+...+1/x2016^2=1CM trong các số từ x1->x2016 có ít nhất 2 số bằng nhau
Cho các số x1,x2,x3 thỏa mãn x1-1/3=x2-2/2=x3-3/1 và x1+x2+x3=30 . Khi đó x1+x2-x2+x3=???
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
đạt cực trị tại các điểm
x
1
,
x
2
thỏa mãn
x
1
∈
-
1
;
0
,
x...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực trị tại các điểm x 1 , x 2 thỏa mãn x 1 ∈ - 1 ; 0 , x 2 ∈ 1 ; 2 . Biết hàm số đồng biến trên ( x 1 , x 2 ). Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Trong các khẳng định sau, khẳng định nào đúng?
A. a < 0 , b > 0 , c > 0 , d < 0
B. a < 0 , b < 0 , c > 0 , d < 0
C. a > 0 , b > 0 , c > 0 , d < 0
D. a < 0 , b > 0 , c < 0 , d < 0
Đáp án A
Đồ thị cắt trục tung tại điểm có tung độ âm ⇒ y 0 = d < 0
Ta có y ' = 3 a x 2 + 3 b x + c , y ' = 0 ⇔ x 1 + x 2 = - 2 b 3 a x 1 . x 2 = c 3 a . Mà y ' > 0 , ∀ x ∈ x 1 , x 2 ⇒ a < 0
Mặt khác x 1 + x 2 > 0 x 1 . x 2 < 0 ⇒ - 2 b 3 a > 0 c 3 a < 0 ⇔ b > 0 c < 0 . Vậy a < 0 , b > 0 , c > 0 , d < 0 .
Đúng 0
Bình luận (0)
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
đạt cực trị tại các điểm
x
1
,
x
2
thỏa mãn
x
1
∈
-
1
;
0
;
x...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực trị tại các điểm x 1 , x 2 thỏa mãn x 1 ∈ - 1 ; 0 ; x 2 ∈ 1 ; 2 . Biết hàm số đồng biến trên khoảng x 1 ; x 2 . Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Trong các khẳng định sau, khẳng định nào đúng?
A. a < 0 , b > 0 , c > 0 , d < 0
B. a < 0 , b < 0 , c > 0 , d < 0
C. a < 0 , b < 0 , c < 0 , d < 0
D. a < 0 , b > 0 , c < 0 , d < 0
Cho cấu hình của nguyên tử các nguyên tố
X
1
,
X
2
,
X
3
,
X
4
,
X
5
:
X
1
:
1
s
2
;
X...
Đọc tiếp
Cho cấu hình của nguyên tử các nguyên tố X 1 , X 2 , X 3 , X 4 , X 5 :
X 1 : 1 s 2 ;
X 2 : 1 s 2 2 s 1 ;
X 3 : 1 s 2 2 s 2 2 p 6 3 s 2 3 p 3 ;
X 4 : 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 4 s 2 ;
X 5 : 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 3 d 7 4 s 2 ;
Trong các nguyên tố cho ở trên, số các nguyên tố kim loại là
A. 2
B. 3
C. 4
D. 5
Cho hàm số
y
x
3
+
2
m
-
2
x
2
-
5
x
+
1
. Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị
x
1
;
x
2
x
1...
Đọc tiếp
Cho hàm số y = x 3 + 2 m - 2 x 2 - 5 x + 1 . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị x 1 ; x 2 x 1 < x 2 thỏa mãn x 1 - x 2 = - 2
A. 7/2
B. - 1
C. 1/2
D. 5
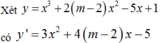
Từ yêu cầu bài toán suy ra phương trình y ' = 0 có hai nghiệm phân biệt x 1 x 2 thỏa mãn x 1 - x 2 = - 2 .
Nhận thấy phương trình
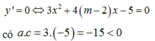
nên y ' = 0 có hai nghiệm trái dấu x 1 < 0 < x 2
Theo hệ thức Vi-ét ta có

Chọn C.
Đúng 0
Bình luận (0)
cho pt x2-2(m-1)x-2m+5=0với m là tham số tìm các giá trị của m để pt đã cho có 2 nghiệm phân biệt x1,x2(x1<x2) thoả mãn x1-x2=-2
Δ=(2m-2)^2-4(-2m+5)
=4m^2-8m+4+8m-20=4m^2-16
Để PT có hai nghiệm phân biệt thì 4m^2-16>0
=>m>2 hoặc m<-2
x1-x2=-2
=>(x1-x2)^2=4
=>(x1+x2)^2-4x1x2=4
=>(2m-2)^2-4(-2m+5)=4
=>4m^2-8m+4+8m-20=4
=>4m^2=20
=>m^2=5
=>m=căn 5 hoặc m=-căn 5
Đúng 0
Bình luận (0)













