Cho ΔABC cân tại A. M là trung điểm của BC. Cho AB=3cm; AC=4cm. Tính AM (Không dùng định lý đường trung tuyến ứng với cạnh huyền của Δvuông, dùng định lí đường trung bình)

Những câu hỏi liên quan
cho ΔABC vuông tại A, biết AB=3cm, AC=4 cm, đường trung tuyến AD ( D ∈BC). Gọi M và N lần lượt là hình chiếu của D Trên AB và AC
a) tính BC, AD
b) chứng minh AD=MN
c) nếu ΔABC vuông cân tại A thì tứ giác BMNC là hình gì ? tại sao ?
a. Pytago: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
AD là trung tuyến ứng cạnh huyền BC nên \(AD=\dfrac{1}{2}BC=2,5\left(cm\right)\)
b. Vì \(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\) nên AMDN là hcn
Vậy AD=MN
c. ABC vuông cân A thì AD là trung tuyến cũng là p/g
Do đó AMDN là hình thoi(1)
Lại có D là trung điểm BC,DM//AC(⊥AB) nên M là trung điểm AB
Cmtt ta được N là trung điểm AC
Mà AB=AC nên AM=AC
Kết hợp (1) ta được AMDN là hình vuông
Đúng 3
Bình luận (0)
Cho ΔABC vuông tại A,(AB<BC). M là trung điểm của BC.Kẻ MF vuông góc với AB,Kẻ ME vuông với AC
a)Tứ giác AEMF là hình gì?
b)cho AB= 3cm,AC=4cm.Tính độ dài AM
c) Gọi I là trung điểm của MF.Chứng minh 3 điểm B,I,E thẳng hàng
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
Đúng 1
Bình luận (0)
b: \(AM=\dfrac{BC}{2}=\dfrac{\sqrt{3^2+4^2}}{2}=2.5\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A, có BC 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho
D
M
E
^
A
B
C
^
. Tính BD.CE bằng A.
2
a
2
B. 3a C.
a
2
D.
4
a
2
Đọc tiếp
Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho D M E ^ = A B C ^ . Tính BD.CE bằng
A. 2 a 2
B. 3a
C. a 2
D. 4 a 2
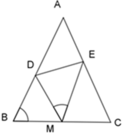
+ Ta có: D M C ^ = D M E ^ + E M C ^
Mặt khác: D M C ^ = A B C ^ + B D M ^ (góc ngoài tam giác)
Mà: D M E ^ = A B C ^ (gt) nên B D M ^ = E M C ^
+ Ta có: A B C ^ = A C B ^ (ΔABC cân tại A) và B D M ^ = E M C ^ (cmt)
=> ΔBDM ~ ΔCME (g - g)
=> B D C M = B M C E => BD.CE = CM.BM
Lại có M là trung điểm của BC và BC = 2a => BM = MC = a
=> BD.CE = a 2 không đổi
Đáp án: C
Đúng 0
Bình luận (0)
Bài 5: Cho ΔABC vuông tại A có AB = 3cm, BC = 5cm.
a) Tính độ dài đoạn AC.
b) Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ΔADC = ΔABC.
c) Gọi M là trung điểm của CD. Qua D vẽ đường thẳng song song với BC cắt BM tại E.
Chứng minh ΔCDE cân tại D.
d) Gọi I là giao điểm của AC và BE. Chứng minh BC + BD > 6.IM.
a) Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)
hay AC=4(cm)
Vậy: AC=4cm
b)Xét ΔADC vuông tại A và ΔABC vuông tại A có
CA chung
AD=AB(gt)
Do đó: ΔADC=ΔABC(hai cạnh góc vuông)
c) Xét ΔEMD và ΔBMC có
\(\widehat{EDM}=\widehat{BCM}\)(hai góc so le trong, ED//BC)
MD=MC(M là trung điểm của CD)
\(\widehat{EMD}=\widehat{BMC}\)(hai góc đối đỉnh)
Do đó: ΔEMD=ΔBMC(g-c-g)
Suy ra: ED=BC(hai cạnh tương ứng)
mà BC=CD(ΔCDA=ΔCBA)
nên ED=CD
hay ΔCDE cân tại D
Đúng 2
Bình luận (0)
Bài 8 :
Cho ΔABC cân tại A có M là trung điểm của BC
a) Vẽ hình
b) Chứng minh rằng : AM là đường trung trực của ΔABC
c) Kẻ BH vuông góc với AC (H thuộc AC), CK vuông góc với AB (K thuộc AB). Chứng minh rằng : BH = CK
d) Chứng minh rằng : HK//BC
e) Gọi O là giao điểm của BH và CK
Chứng minh rằng : ba điểm AOM thẳng hàng
Cho ΔABC vuông tại A (AB < AC), M là trung điểm của BC. Gọi D là điểm đối xứng của A qua M. a) Chứng minh tứ giác ABDC là hình chữ nhật. b) Gọi I là điểm đối xứng của A qua BC, AI cắt BC tại H. Chứng minh tứ giác BIDC là hình thang cân.
\(a,\) Vì M là trung điểm AD và BC nên ABDC là hình bình hành
Mà \(\widehat{BAC}=90^0\) nên ABDC là hình chữ nhật
\(b,\) Vì H,M là trung điểm AI và AD nên HM là đường trung bình \(\Delta ADI\)
\(\Rightarrow DI\text{//}HM\) hay \(DI//BC\)
Do đó BIDC là hình thang
Vì I đx với A qua BC nên \(AB=BI\) và BC là trung trực AI
Do đó \(\Delta ABI\) cân tại B
Suy ra BC là trung trực cũng là phân giác
Do đó \(\widehat{ABC}=\widehat{CBI}\left(1\right)\)
Lại có ABDC là hcn nên \(\widehat{BCD}+\widehat{ACB}=\widehat{ACD}=90^0\)
Mà \(\Delta ABC\bot A\) nên \(\widehat{ABC}+\widehat{ACB}=90^0\)
\(\Rightarrow\widehat{BCD}=\widehat{ABC}\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\widehat{CBI}=\widehat{BCD}\)
Vậy BIDC là hình thang cân
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A có M là trung điểm của BC. Kẻ Mx // AC cắt AB tại E và My // AB cắt AC tại F. Chứng minh rằng:
1, E và F lần lượt là trung điểm của AB và AC.
2, EF = 1/2. BC
3, ME = MF ; AE = AF
. Cho ΔABC vuông tại A có AB=12cm, BC=20cm.
a) Tính AC và so sánh các góc của ΔABC.
b) Từ A vẽ đường thẳng vuông góc với BC tại H, trên tia đối của tia HA lấy điểm D sao cho H là trung điểm của AD. Chứng minh ΔBDA cân.
c) Chứng minh ΔDBC vuông.
d) Gọi M là trung điểm của cạnh AB và K là hình chiếu của H trên DC. Chứng minh ba điểm M, H, K thẳng hàng
ABDC E
a) Vì AD phân giác BACˆBAC^ (gt)
=> ABAC=BDDCABAC=BDDC (t/c đường p/g ΔΔ )
=> ABAC+AB=BDBD+DCABAC+AB=BDBD+DC (t/c TLT)
=> 1212+20=BDBC1212+20=BDBC
=> 1232=BD281232=BD28
=> BD=12⋅2832=10,5BD=12⋅2832=10,5 cm
Ta có: BD+DC=BCBD+DC=BC (D ∈∈ BC)
=> DC=28−10,5=17,5DC=28−10,5=17,5 cm
Xét ΔΔ ABC có: DE // AB (gt)
=> DEAB=DCBCDEAB=DCBC (hệ qủa ĐL Ta-lét)
=> DE=AB⋅DCBC=12⋅17,528=7,5DE=AB⋅DCBC=12⋅17,528=7,5 cm

Nguồn : hh
~ Chúc you học tốt ~
:)))
Vào TKHĐ của mình là thấy nha
:>>>
#Hoc_tot#
Xem thêm câu trả lời
Cho ΔABC cân tại A (A nhọn ). TPG của góc A cắt BC tại I
a, CM AI vuông BC
b, Gọi D là trung điểm của AC , M là giao điểm của BC vs AI . CM rằng M là trọng tâm của tam giác ABC
c, Biết AB = AC = 5 cm : BC = 6 cm . Tính AM
a) Có: △ABC cân tại A => AB=AC
và AI là tia p/g của góc ABC => góc BAI= góc CAI
Xét △ABI và △ ACI có
AI chung
góc BAI= góc CAI
AB=AC
=>△ABI = △ ACI (c.g.c)
b)Có : △ABC cân tại A ; AI là tia p/g của góc ABC
=> AI cũng là đường trung tuyến của △ABC
có :D là trung điểm của AC
=> BD là đường trung tuyến của △ ABC
trong △ABC có
AI là đường trung tuyến thứ nhất
BD là đường trung tuyến thứ hai
Mà 2 đường này cắt nhau tại M
=> M là trọng tâm của △ABC
BI=CI=BC/2=3(cm)
Có : △ABC cân tại A ; AI là tia p/g của góc ABC
=> AI cũng là đường cao
=> AI⊥BC
=> △ABI vuông tại I
=> AI^2+ BI^2= AB^2
=> AI^2+9=25
AI^2 = 16
=> AI = 4( cm)
Đúng 1
Bình luận (0)



















