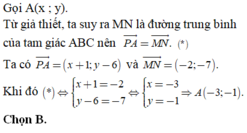Cho tam giác ABC có tọa độ các trung điểm các cạnh là M(2;1) N(5;3) P(3;-4) a) Lập phương trình chính tắc các cạnh của tam giác ABC

Những câu hỏi liên quan
Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; -4); P(-1; 6) lần lượt là trung điểm của các cạnh BC; CA; AB. Tìm tọa độ đỉnh A?
A. A(1; 5)
B. A(-3; -1)
C. A(-2; -7)
D. A(1; -10)
Câu 6: Cho tàm giác ABC có A(1; - 1) ;B(2; 0) ;C(3; 5) a) Tìm tọa độ các vecto AB ,AC ,BC b) Tính độ dài các cạnh của tam giác ABC. Từ đó tính chu vi tam giác. c) Tìm tọa độ trung điểm các cạnh và tìm tọa độ trọng tâm của tam giác ABC. d) Tìm tọa độ điểm D để tứ giác ABCD là hnh bình hành e) Tọa độ chân đường cao xuất phát từ A của tam giác. Đ) Tính góc A?
a: vecto AB=(1;1)
vecto AC=(2;6)
vecto BC=(1;5)
b: \(AB=\sqrt{1^2+1^2}=\sqrt{2}\)
\(AC=\sqrt{2^2+6^2}=2\sqrt{10}\)
\(BC=\sqrt{1^2+5^2}=\sqrt{26}\)
=>\(C=\sqrt{2}+2\sqrt{10}+\sqrt{26}\)
c: Tọa độ trung điểm của AB là:
x=(1+2)/2=1,5 và y=(-1+0)/2=-0,5
Tọa độ trung điểm của AC là;
x=(1+3)/2=2 và y=(-1+5)/2=4/2=2
Tọa độ trung điểm của BC là:
x=(2+3)/2=2,5 và y=(0+5)/2=2,5
d: ABCD là hình bình hành
=>vecto AB=vecto DC
=>3-x=1 và 5-y=1
=>x=2 và y=4
Đúng 1
Bình luận (0)
Cho M(2; 0), N(2; 2), P(–1; 3) là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tọa độ điểm B là:
A. B(1; 1)
B. B(–1; –1)
C. B(–1; 1)
D. B(–1; 5)
Tam giác ABC có M; N; P lần lượt là trung điểm của BC; AC ; AB nên PN và MN là đường trung bình của tam giác.
Suy ra: PN// BC và MN// AB.
Khi đó, tứ giác PNMB là hình bình hành.
Do đó, P B → = N M → với P B → ( x + 1 ; y − 3 ) ; N M → ( 0 ; − 2 )
⇒ x + 1 = 0 y − 3 = − 2 ⇔ x = − 1 y = 1 ⇒ B ( − 1 ; 1 )
Đáp án C
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(1;1), B(-3;5) và M(1/2;-3/2) là trung điểm của AC.
a,Tìm tọa độ đỉnh C của tam giác ABC
b,Lập phương trình các cạnh của tam giác ABC
c,Tính khoảng cách từ B đến cạnh AC
cho tam giác ABC vuông tại A có I là trung điểm của cạnh BC. gọi M là trung điểm của IB và N là điểm nằm trên đoạn thẳng IC sao cho NC=2NI. biết rằng M(11/2;-4), phương trình đường thẳng AN là x-y-2=0 và điểm A có hoành độ âm. tìm tọa độ các đỉnh của tam giác ABC
Cho tam giác ABC có các điểm \(M\left( {2;2} \right),N\left( {3;4} \right),P\left( {5;3} \right)\) lần lượt là trung điểm của các cạnh AB, BC và CA
a) Tìm tọa độ các đỉnh của tam giác
b) Chứng minh rằng trọng tâm của các tam giác ABC và MNP trùng nhau
c) Giải tam giác ABC
a) Gọi tọa độ các điểm như sau: \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\)
\(M\left( {2;2} \right),N\left( {3;4} \right),P\left( {5;3} \right)\) lần lượt là trung điểm của các cạnh AB, BC và CA nên ta có:
\(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}=4\\{x_A} + {x_C} = 2{x_P}=10\\{x_C} + {x_B} = 2{x_N}=6\\{y_A} + {y_B} = 2{y_M}=4\\{y_A} + {y_C} = 2{y_P}=8\\{y_C} + {y_B} = 2{y_N}=6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 4\\{x_C} - {x_B} = 6\\{x_C} + {x_B} = 6\\{y_A} + {y_B} = 4\\{y_C} - {y_B} = 4\\{y_C} + {y_B} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 4\\{x_B} = 0\\{x_C} = 6\\{y_A} = 3\\{y_B} = 1\\{y_C} = 5\end{array} \right.\)
Vậy các đỉnh của tam giác có tọa độ là \(A\left( {4;3} \right),B\left( {0;1} \right),C\left( {6;5} \right)\)
b) Gọi \(G\left( {{x_G};{y_G}} \right),G'\left( {{x_{G'}};{y_{G'}}} \right)\) là trọng tâm của hai tam giác ABC và MNP
Áp dụng tính chất trọng tâm ta có:
\(\begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{4 + 0 + 6}}{3} = \frac{{10}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{3 + 1 + 5}}{3} = 3\\{x_{G'}} = \frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 3 + 5}}{3} = \frac{{10}}{3};{y_{G'}} = \frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{2 + 4 + 3}}{3} = 3\end{array}\)
Suy ra \(G\left( {\frac{{10}}{3};3} \right)\) và \(G'\left( {\frac{{10}}{3};3} \right)\), tọa độ của chúng bằng nhau nên hai điểm G và G’ trùng nhau (đpcm)
c) Ta có: \(\overrightarrow {AB} = \left( { - 4; - 2} \right),\overrightarrow {AC} = \left( {2;2} \right),\overrightarrow {BC} = \left( {6;4} \right)\)
Suy ra: \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{( - 4)}^2} + {{( - 2)}^2}} = 2\sqrt 5 ,AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)
\(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{6^2} + {4^2}} = 2\sqrt {13} \)
\(\begin{array}{l}\cos A = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{( - 4).2 + ( - 2).2}}{{2\sqrt 5 .2\sqrt 2 }} = - \frac{{3\sqrt {10} }}{{10}} \Rightarrow \widehat A \approx 161^\circ 33'\\\cos B = \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{BA.BC}} = \frac{{4.6 + 2.4}}{{2\sqrt 5 .2\sqrt {13} }} = \frac{{8\sqrt {65} }}{{65}} \Rightarrow \widehat B = 7^\circ 7'\\\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 161^\circ 33' - 7^\circ 7' = 11^\circ 20'\end{array}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
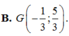
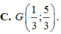
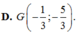
Cho M(2 ; 0) : N( 2 ; 2) và P( -1 ; 3) lần lượt là trung điểm các cạnh BC ; CA ; AB của tam giác ABC. Tọa độ B là:
A.(1;1)
B.(-1;-1)
C.(-1;1)
D. (1;-1)
anh em giúp mình vớiCho tam giác ABC có 2;2A , 6; 2B , 4; 2C . 1. Tìm tọa độ trung điểm các cạnh và tọa độ trọng tâm tam giác. 2. Chứng minh tam giác ABC vuông 3. Tính chu vi và diện tích tam giác. 4. Tìm tọa độ điểm D sao cho ABCD là hình chữ nhật. 5. Tìm tọa độ điểm M sao cho 2 0 MA MB MC . 6. Tìm tọa độ điểm N thuộc cạnh AB sao cho 2 NA NB NC nhỏ nhất. 7. Tìm tọa độ điểm P trên trục tung sao cho PA PC nhỏ nhất .
Đọc tiếp
anh em giúp mình với
Cho tam giác ABC có 2;2A , 6; 2B , 4; 2C .
1. Tìm tọa độ trung điểm các cạnh và tọa độ trọng tâm tam giác. 2. Chứng minh tam giác ABC vuông 3. Tính chu vi và diện tích tam giác. 4. Tìm tọa độ điểm D sao cho ABCD là hình chữ nhật. 5. Tìm tọa độ điểm M sao cho 2 0 MA MB MC . 6. Tìm tọa độ điểm N thuộc cạnh AB sao cho 2 NA NB NC
nhỏ nhất.
7. Tìm tọa độ điểm P trên trục tung sao cho PA PC nhỏ nhất .