Giải thích vì sao trục khuỷu quay được n vòng thì pít tông đi được 2n hành trình

Những câu hỏi liên quan
Tìm mối liên hệ giữa hành trình pít tông S và bán kính quay R của trục khuỷu.
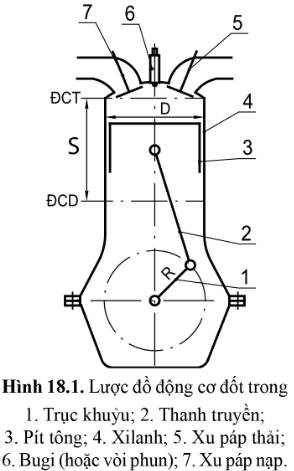
1, Khi pít-tông ở điểm cao nhất và thấp nhất, vị trí của thanh truyền và tay quay như thế nào
2. Tại sao khi quay tay quay thì van nạp và van thải lại đóng, mở được? Để van nạp và van thải đóng mở 1 lần thì trục khuỷu phảo quay mấy vòng?
Khi pit-tông dịch chuyển được 1 hành trình thì trục khuỷu sẽ quay góc:
A. 90ᵒ
B. 180ᵒ
C. 360ᵒ
D. 720ᵒ
Nêu cấu tạo của pittong,thanh truyền, trục khuỷu? Khi pittong dịch chuyển được 2 hành trình thì trục khuỷu quay được mấy vòng?
1. Khi pít-tông ở điểm cao nhất vào thấp nhất , vị trí của thanh truyền và tay quay như thế nào ?
2. Tại sao khi quay tay quay thì van nạp và van thải lại đóng , mở được ? Để van nạp và van thải đóng
mở một lần thì trục khuỷu phải quay mấy vòng ?
Khi piston ở điểm cao nhất và thấp nhất thì vị trí của trục khuỷu và tay quay có 1 điểm chung là tay quay sẽ vuông góc với thanh ngang (tay ngang) của trục khuỷu khi nhìn vào hình chiếu ngang (theo đúng kỹ thuật là hình chiếu đứng). Nhưng lúc này có 2 điểm để phân biệt:
1. Khi piston ở vị trí cao nhất: đỉnh của tay quay (phần nối với piston) sẽ xa thanh ngang nhất.
2. Khi piston ở vị trí thấp nhất: đỉnh của tay quay (phần nối với piston) sẽ gần thanh ngang nhất.
Đúng 0
Bình luận (0)
2. Khi quay tay quay, một bánh xích gắn liền với tay quay sẽ dẫn động trục cam, thông qua sên cam. Các cam trên thân trục cam khi đó sẽ nén hoặc nhả các van nạp và van thải để điều khiển chúng đóng mở chính xác theo chu trình hoạt động của động cơ.
3. Trong một chu trình hút, nén nổ, xả thì trục khuỷu phải quay 2 vòng. Trong khi đó van nạp chỉ đóng mở có 1 lần. Tương tự cho van xả
Đúng 0
Bình luận (0)
Ở động cơ 4 kì, khi trục khuỷu quay được 1 vòng thì pittong dịch chuyển bao nhiêu hành trình ạ?
Trong động cơ 4 kỳ, khi trục khuỷu quay được một vòng, piston sẽ di chuyển hai lần, một lần đi lên và một lần đi xuống. Do đó, piston sẽ di chuyển một quãng đường bằng với chiều dài của xi lanh, tương đương với hai lần hành trình của piston.
Vì vậy, khi trục khuỷu quay được 1 vòng, piston sẽ dịch chuyển một hành trình bằng với độ dài của xi lanh.
Đúng 1
Bình luận (0)
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho alpha là góc quay của trục khuỷu, O là vị trí của pít – tông khi alpha frac{pi }{2} và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.a) Biết IA 8cm, viết công thức tính tọa độ {x_M}của điểm M trên trục Ox theo alpha .b) Ban đầu alpha 0. Sau 1 phút chuyển động,...
Đọc tiếp
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho \(\alpha \) là góc quay của trục khuỷu, O là vị trí của pít – tông khi \(\alpha = \frac{\pi }{2}\) và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.
a) Biết IA = 8cm, viết công thức tính tọa độ \({x_M}\)của điểm M trên trục Ox theo \(\alpha \).
b) Ban đầu \(\alpha = 0\). Sau 1 phút chuyển động, \({x_M}\)= – 3cm. Xác định\({x_M}\) sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười
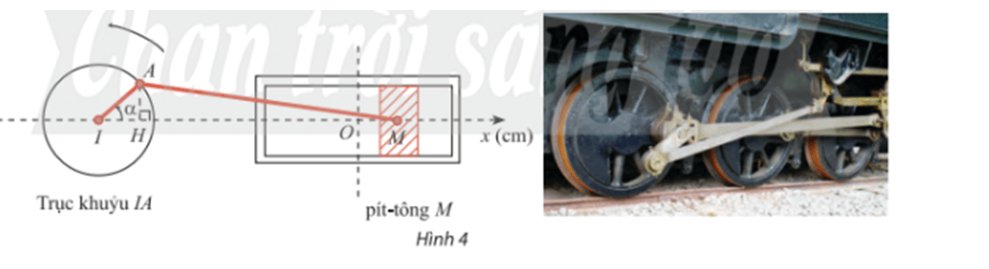
a, Tại \(\alpha = \frac{\pi }{2}\) thì H trùng I, M trùng O nên MH = OI do đó OM = IH.
Xét tam giác AHI vuông tại H có: \(IH = cos\alpha .IA = 8cos\alpha .\)
\( \Rightarrow {x_M} = OM = IH = 8cos\alpha \)
b, Sau khi chuyển động được 1 phút, trục khuỷu quay được một góc là \(\alpha \)
Khi đó \({x_M} = - 3cm \Rightarrow cos\alpha = - \frac{3}{8}\)
Sau khi chuyển động 2 phút, trục khuỷu quay được một góc \(2\alpha \), nên:
\({x_M} = 8cos2\alpha = 8\left( {2{{\cos }^2}\alpha - 1} \right)\)\( = 8\left( {2{{\left( { - \frac{3}{8}} \right)}^2} - 1} \right) \approx - 5,8 cm\)
Đúng 0
Bình luận (0)
Quan sát Hình 18.2 và cho biết hình nào có đỉnh pít tông xa tâm trục khuỷu nhất và hình nào có đỉnh pít tông gân tâm trục khuỷu nhất?
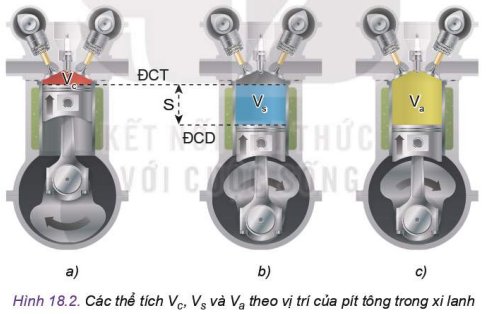
- Hình a có đỉnh pit tông ở xa tâm trục khuỷu nhất.
- Hình b, c có đỉnh pit tông gần tâm trục khuỷu nhất.
Đúng 0
Bình luận (0)
Pít-tông của một động cơ đốt trong dao động trên một đoạn thẳng dài 16cm và làm cho trục khuỷu của động cơ quay đều (Hình 1.5). Xác định biên độ dao động của một điểm trên mặt pít-tông.
Dao động trên một đường thẳng dài `16 cm`
`=>L=16 (cm)`
Mà `A=L/2`
`=>A=16/2=8` (cm)
Đúng 1
Bình luận (0)

















