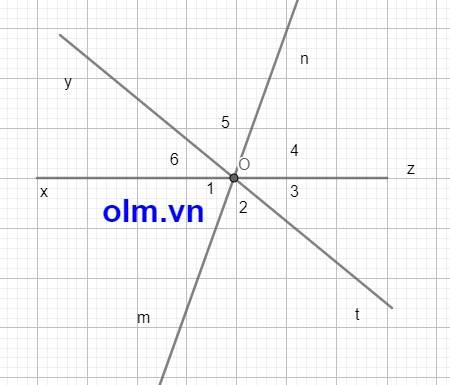
vẽ 2 góc kề bù \(xOy;yOy\) biết \(\widehat{xOy}=118^0\) . tính yOy

Những câu hỏi liên quan
vẽ 2 góc kề bù xoy và yoy là góc kề bù, biết xoy = 118 độ, tính yoy
\(\widehat{yOy}=180^0-\widehat{xOy}=180^0-118^0=62^0\)
Đúng 0
Bình luận (0)
Vì xOy kề bù với yoy nên ta ó:
xOy+ yOy= 180 độ
118 + yOy=180
yOy=180-118
yOy= 62 độ
Đúng 0
Bình luận (0)
bài 1 cho góc xOy, vẽ xOz kề bù với góc xÔy, vẽ góc zOt kề bù với góc xOz. Chứng minh góc xOy và tOz là 2 góc đối đỉnh
Vì góc xOz kề bù với xOy
=> \(\widehat{xOy}=180-\widehat{xOz}\)
Vì góc zOt kề bù với góc xOz
=> \(\widehat{zOt}=180-\widehat{xOz}\)
=> \(\widehat{xOy}=\widehat{zOt}\)
=> \(\widehat{xOy}\text{đối đỉnh}\widehat{zOt}\)
Đúng 0
Bình luận (0)
A) cho góc mOn . Vẽ góc nOt kề bù với góc mOn . Vẽ góc mOz kề bù với góc mOn . Khiu đó mOn và tOz có phải là hai góc đối đỉnh ko?b)Cho góc hBk. vẽ Bm là tia phân giác của góc hBk . vẽ Bm là tia đối của tia Bm. Vẽ góc kBj kề bù với góc hBk. khi đó các góc mBj và hBm có phải là hai góc đối đỉnh koc)cho góc xOy vẽ góc yOz kề bù với góc xOy vẽ gos xOt kề bù với góc xOy. Vẽ Om kề bù với góc zOy vẽ Om là tia phân giác của góc tOxkhi đó zOn và xOm có phải là 2 góc đối đỉnh ko
Đọc tiếp
A) cho góc mOn . Vẽ góc nOt kề bù với góc mOn . Vẽ góc mOz kề bù với góc mOn . Khiu đó mOn và tOz có phải là hai góc đối đỉnh ko?
b)Cho góc hBk. vẽ Bm là tia phân giác của góc hBk . vẽ Bm' là tia đối của tia Bm. Vẽ góc kBj kề bù với góc hBk. khi đó các góc m'Bj và hBm có phải là hai góc đối đỉnh ko
c)cho góc xOy vẽ góc yOz kề bù với góc xOy vẽ gos xOt kề bù với góc xOy. Vẽ Om kề bù với góc zOy vẽ Om là tia phân giác của góc tOxkhi đó zOn và xOm có phải là 2 góc đối đỉnh ko
Ta có:
\(\widehat{mOz}\) kề bù với \(\widehat{mOn}\)
\(\widehat{nOt}\) kề bù với \(\widehat{mOn}\)
\(\Rightarrow\) \(\widehat{mOz}\) và \(\widehat{nOt}\) đối đỉnh
Đúng 0
Bình luận (0)
Cho góc xOy . Vẽ góc yOz kề bù với xOy . Vẽ góc xOt kề bù với với góc xOy . Vẽ On là phân giác của góc yOz . Vẽ Om là phân giác của góc xOt .Khi đó góc zOn và xOm có phải là 2 góc đối đỉnh không
Vì góc yOz và góc xOy là hai góc kề bù nên Oz và Ox cùng nằm trên một đường thẳng zx (1)
Tương tự ta có: Ot và Oy cùng nằm trên một đường thẳng
\(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh
⇒ \(\widehat{O_2}\) = \(\dfrac{1}{2}\) \(\widehat{xOt}\) = \(\dfrac{1}{2}\) \(\widehat{yOz}\) = \(\widehat{O_5}\)
Mặt khác ta có: \(\widehat{O_2}\) + \(\widehat{O_1}\) + \(\widehat{O_6}\) = 1800 (gt)
⇒ \(\widehat{O_1}\) + \(\widehat{O_6}\) + \(\widehat{O_5}\) = 1800
⇒ Om và On cùng thuộc một đường thẳng mn (2)
Kết hợp (1) và (2) ta có: góc zOn và góc xOm là hai góc đối đỉnh
Đúng 1
Bình luận (0)
a) Cho góc mOn. Vẽ góc nOt kề bù vs góc mOn. Vẽ góc mOz kề bù vs góc mOn. Khi đó mOn và tOz có phải là 2 góc đối đỉnh ko?b) Cho góc hBk. Vẽ Bm là tia phân giác của góc hBk. Vẽ Bm là tia đối của tia Bm. Vẽ góc kBj kề bù vs góc hBk. Khi đó các góc mBj và hBm có phải là hai góc đối đỉnh ko?c) Cho góc xOy. Vẽ góc yOz kề bù vs góc xOy. Vẽ góc xOt kề bù vs góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có fai là 2 góc đối đỉnh ko?
Đọc tiếp
a) Cho góc mOn. Vẽ góc nOt kề bù vs góc mOn. Vẽ góc mOz kề bù vs góc mOn. Khi đó mOn và tOz có phải là 2 góc đối đỉnh ko?
b) Cho góc hBk. Vẽ Bm là tia phân giác của góc hBk. Vẽ Bm' là tia đối của tia Bm. Vẽ góc kBj kề bù vs góc hBk. Khi đó các góc m'Bj và hBm có phải là hai góc đối đỉnh ko?
c) Cho góc xOy. Vẽ góc yOz kề bù vs góc xOy. Vẽ góc xOt kề bù vs góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có fai là 2 góc đối đỉnh ko?
a)
Có vì :
+) mOn kề bù với góc mOz nên On và Oz đối nhau (1)
+) mOn kề bù với nOt nên Om đối Ot (2)
Vì Om đố Ot; On dối Oz nên 2 gốc nOm và tOz dối đỉnh (đpcm)
Đúng 0
Bình luận (0)
Tự vẽ hình.
a) Ta thấy: Góc nOt kề bù vs góc mOn, góc mOz kề bù vs góc mOn
=> Góc nOt = Góc mOz. (1)
Góc nOt + Góc mOn = 180 độ (kề bù) (2)
Góc mOz + Góc tOz = 180 độ ( kề bù) (3)
Từ (1) ; (2) ; (3) suy ra Góc mOn = Góc zOt
=> mOt cắt zOn tại O
Vậy: mOn và tOz là 2 góc đối đỉnh
b,c tương tự
Đúng 0
Bình luận (0)
a) Cho góc mOn. Vẽ góc nOt kề bù vs góc mOn. Vẽ góc mOz kề bù vs góc mOn. Khi đó mOn và tOz có phải là 2 góc đối đỉnh ko?b) Cho góc hBk. Vẽ Bm là tia phân giác của góc hBk. Vẽ Bm là tia đối của tia Bm. Vẽ góc kBj kề bù vs góc hBk. Khi đó các góc mBj và hBm có phải là hai góc đối đỉnh ko?c) Cho góc xOy. Vẽ góc yOz kề bù vs góc xOy. Vẽ góc xOt kề bù vs góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có fai là 2 góc đối đỉnh ko?
Đọc tiếp
a) Cho góc mOn. Vẽ góc nOt kề bù vs góc mOn. Vẽ góc mOz kề bù vs góc mOn. Khi đó mOn và tOz có phải là 2 góc đối đỉnh ko?
b) Cho góc hBk. Vẽ Bm là tia phân giác của góc hBk. Vẽ Bm' là tia đối của tia Bm. Vẽ góc kBj kề bù vs góc hBk. Khi đó các góc m'Bj và hBm có phải là hai góc đối đỉnh ko?
c) Cho góc xOy. Vẽ góc yOz kề bù vs góc xOy. Vẽ góc xOt kề bù vs góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có fai là 2 góc đối đỉnh ko?
Bài 2: vẽ góc tù góc xOy, lấy N nằm trong góc xOy. Kẻ d1 kề bù Ox, d2 kề bù Oy
Cho góc xoy=70 độ.Vẽ góc xoz kề bù với góc xoy
Vẽ góc yot kề bù với góc xoy.Tính góc yot
cho góc xOy = 100 độ , vẽ góc yOz kề bù với góc xOy . Góc Ot là tia phân giác của xOy , Ot' là tia phân giác của góc yOz
. 1, Vẽ hình , kể tên các cặp góc kề bù trong hình vẽ .
2 Tính sồ đo góc tOt'
Cặp góc kề bù trong hình vẽ: \(\widehat{xOy};\widehat{zOy}\)
2,
Ot là tia phân giác \(\widehat{xOy}\Rightarrow\widehat{xOt}=\widehat{tOy}=\widehat{xOy}:2=100^o:2=50^o\)
Vì \(\widehat{zOy}\)kề bù \(\widehat{xOy}\Rightarrow\widehat{zOy}+\widehat{xOy}=180^o\Rightarrow\widehat{zoy}+100^o=180^o\Rightarrow\widehat{zOy}=80^o\)
Vì Ot' là tia phân giác \(\widehat{zOy}\Rightarrow\widehat{t'Oy}=\widehat{t'Oz}=\widehat{zOy}:2\Rightarrow80^o:2=40^o\)
Vì Oz và Ox đối nhau => tia Oy nằm giữa Oz; Ox => Oy cũng nằm giữa Ot; Ot'
\(\Rightarrow\widehat{t'Oy}+\widehat{tOy}=\widehat{tOt'}\Rightarrow40^o+50^o=\widehat{tOt'}\Rightarrow\widehat{tOt'}=90^o\)
Cho góc xOy. Vẽ góc yOz kề bù với xOy. Vẽ góc xOt kề bù với góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có phải là hai góc đối đỉnh không?
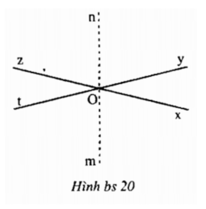
Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, hai góc zOy và tOx là hai góc đối đỉnh nên ∠zOy = ∠tOx.
Vì On, Om lần lượt là tia phân giác của góc zOy, góc xOt và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180° hay ∠mOn = 180º.
Suy ra Om và On là hai tia đối nhau.
Từ đó, hai góc ∠zOn và ∠mOx là hai góc đối đỉnh.
Đúng 0
Bình luận (0)