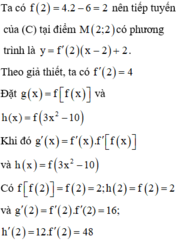Giải từng phương trình tuyến tính đồng thời sau đây bằng phương pháp đồ thị:

Những câu hỏi liên quan
Giải hệ phương trình sau bằng phương pháp đồ thị và phương pháp thế
\(\left\{{}\begin{matrix}2x-y=5\\x+2y=5\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2x-y=5\\x+2y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-5\\x+2\left(2x-5\right)=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-5\\x+4x-10=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-5\\5x-10=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-5\\5x=15\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-5\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2\cdot3-5\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\) là nghiệm duy nhất của hệ phương trình.
Đúng 1
Bình luận (0)
Cho đồ thị (C) của hàm số
y
x
3
3
−
2
x
2
+
3
x
+
1.
Phương trình tiếp tuyến của (C) song song với đường thẳng
y
3
x
+
1
là phương trình nào sau đây? A.
y
3
x
−
1
B.
y...
Đọc tiếp
Cho đồ thị (C) của hàm số y = x 3 3 − 2 x 2 + 3 x + 1. Phương trình tiếp tuyến của (C) song song với đường thẳng y = 3 x + 1 là phương trình nào sau đây?
A. y = 3 x − 1
B. y = 3 x
C. y = 3 x − 29 3
D. y = 3 x + 29 3
Đáp án C
Gọi d là tiếp tuyến của C tại M x 0 ; y 0 thỏa mãn đề bài
Ta có y ' = x 2 − 4 x + 3 ⇒ y ' x 0 = x 0 2 − 4 x 0 + 3 = k d là hệ số góc của d
d / / y = 3 x + 1 ⇒ k d = x 0 2 − 4 x 0 + 3 = 3 ⇔ x 0 = 0 x 0 = 4
Với x 0 = 0 ⇒ M 0 ; 1 ⇒ d : 3 x − 0 + 1 ⇔ d : y = 3 x + 1 ≡ y = 3 x + 1
Với x 0 = 4 ⇒ M 4 ; 7 3 ⇒ d : 3 x − 4 + 7 3 ⇔ d : y = 3 x − 29 3
Vậy d : y = 3 x − 29 3
Đúng 0
Bình luận (0)
Cho đồ thị (C)của hàm số
y
x
3
3
−
2
x
2
+
3
x
+
1.
Phương trình tiếp tuyến của (C)song song với đường thẳng
y
3
x
+
1
là phương trình nào sau đây? A.
y
3
x
−
1
B.
y...
Đọc tiếp
Cho đồ thị (C)của hàm số y = x 3 3 − 2 x 2 + 3 x + 1. Phương trình tiếp tuyến của (C)song song với đường thẳng y = 3 x + 1 là phương trình nào sau đây?
A. y = 3 x − 1
B. y = 3 x
C. y = 3 x − 29 3
D. y = 3 x + 29 3
Đáp án C
Gọi d là tiếp tuyến của (C) tại M x 0 ; y 0 thỏa mã đề bài.
Ta có y ' = x 2 − 4 x + 3 ⇒ y ' x 0 = x 0 2 − 4 x 0 + 3 = k d là hệ số góc của d.
d / / y = 3 x + 1 ⇒ k d = 3 ⇔ x 0 2 − 4 x 0 + 3 = 3 ⇔ x 0 = 0 x 0 = 4 .
Với x 0 = 0 ⇒ M 0 ; 1 ⇒ d : y = 3 y − 0 + 1 ⇔ d : y = 3 x + 1 ≡ y = 3 x + 1.
Với x 0 = 4 ⇒ M 4 ; 7 3 ⇒ d : y = 3 y − 4 + 7 3 ⇔ d : y = 3 x − 29 3 .
Suy ra d : y = 3 x − 29 3 .
Đúng 0
Bình luận (0)
Giải các bất phương trình sau bằng đồ thị:
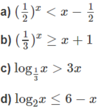
a) Vẽ đồ thị của hàm số 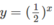 và đường thẳng
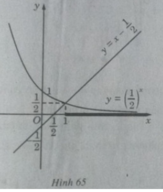
và đường thẳng 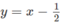 trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số 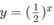 nằm phía dưới đường thẳng
nằm phía dưới đường thẳng 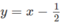 . Vậy tập nghiệm của bất phương trình đã cho là (1;+∞)
. Vậy tập nghiệm của bất phương trình đã cho là (1;+∞)
b) Vẽ đồ thị của hàm số 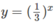 và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
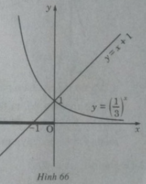
Khi x < 0 đồ thị của hàm số 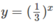 nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-∞;0]
nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-∞;0]
c) Vẽ đồ thị của hàm số 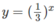 và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = 1/3 (H.67)
và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = 1/3 (H.67)
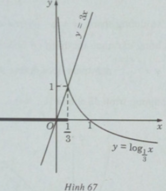
Khi x < 1/3 đồ thị của hàm số 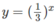 nằm phía trên đường thẳng y = 3x.
nằm phía trên đường thẳng y = 3x.
Vậy tập nghiệm của bất phương trình đã cho là (- ∞ ;1/3).
d) Vẽ đồ thị của hàm số y = log 2 x và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).
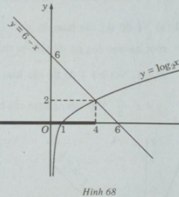
Khi x < 4, đồ thị của hàm số y = log 2 x nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là (- ∞ ;4].
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định và liên tục trên R thỏa mãn đồng thời các điều kiện sau:
f
x
0
∀
x
∈
R
,
f
x
-
e
x
.
f
2
x
∀
x
∈
R
và
f
0
1
2
....
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên R thỏa mãn đồng thời các điều kiện sau: f x > 0 ∀ x ∈ R , f ' x = - e x . f 2 x ∀ x ∈ R và f 0 = 1 2 . Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x 0 = ln 2 là:
A. 2 x + 9 y - 2 ln 2 - 3 = 0
B. 2 x - 9 y - 2 ln 2 + 3 = 0
C. 2 x - 9 y + 2 ln 2 - 3 = 0
D. 2 x - 9 y - 2 ln 2 - 3 = 0
Ethanol có thể được điều chế bằng ba phương pháp theo sơ đồ sau đây:
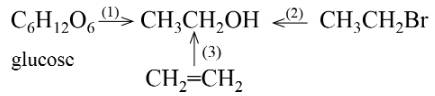
a) Viết phương trình hoá học của quá trình chuyển hoá trên.
b) Ethanol thu được bằng phương pháp nào ở trên được gọi là “ethanol sinh học”? Giải thích.
a.PTHH:
(1) C6H12O6 \(\underrightarrow{enzyme}\) 2C2H5OH + 2CO2
(2) CH3CH2Br + NaOH → C2H5OH + NaBr
(3) CH2=CH2 + H2O\(\underrightarrow{h_2so_4,t^o}\) C2H5OH
b. Ethanol thu được bằng phương pháp (1) ở trên được gọi là "ethanol sinh học" vì đây là phương pháp điều chế ethanol thông qua quá trình lên men các sản phẩm như tinh bột, cellulose, phế phẩm công nghiệp đường, ... thành glucose, sau đó glucose sẽ chuyển hóa thành ethanol theo phương trình (1).
Đúng 1
Bình luận (0)
Vật chuyển động thẳng đều có đồ thị tọa độ - thời gian như hình sau:
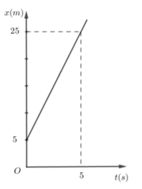
Phương trình chuyển động của vật có dạng nào sau đây?
A. x=5+5t
B. x=4t
C. x=5−5t
D. x=5+4t
Cho hàm số
y
f
x
có đạo hàm trên R và đồ thị
C
. Tiếp tuyến của đồ thị
C
tại điểm
2
;
m
có phương trình là
y
4
x
-
6
. Tiếp tuyến của các đồ thị hàm số
y
f
f
x...
Đọc tiếp
Cho hàm số y = f x có đạo hàm trên R và đồ thị C . Tiếp tuyến của đồ thị C tại điểm 2 ; m có phương trình là y = 4 x - 6 . Tiếp tuyến của các đồ thị hàm số y = f f x và y = f 3 x 2 - 10 tại điểm có hoành độ bằng 2 có phương trình lần lượt là y = a x + b và y = c x + d . Tính giá trị của biểu thức S = 4 a + 3 c - 2 b + d .
A. S = -26
B. S = 176
C. S = 178
D. S = 174
Cho hàm số y f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là
y
4
x
-
6
. Tiếp tuyến của các đồ thị hàm số
y
f
f
x
và
y
f
3
x
2
-
10...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là y = 4 x - 6 . Tiếp tuyến của các đồ thị hàm số y = f f x và y = f 3 x 2 - 10 tại điểm có hoành độ bằng 2 có phương trình lần lượt là y = a x + b v à y = c x + d . Tính giá trị của biểu thức S = 4 a + 3 c - 2 b + d
A. S = -26
B. S = 176
C. S = 178
D. S = 174