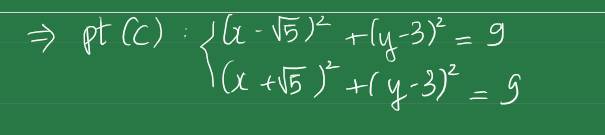Gọi tâm của đường tròn là điểm \(I(a;b)\)

Ta có: \(IA = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} ,d\left( {I,Ox} \right) = b,d\left( {I,Oy} \right) = a\)

Giải hệ phương trình \(\left\{ \begin{array}{l}d\left( {I,Ox} \right) = IA\\d\left( {I,Oy} \right) = IA\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \\a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \end{array} \right.\)

Thay \(a = b\) vào phương trình \(a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \) ta có:

\(\begin{array}{l}a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {a - 2} \right)}^2}} \\ \Rightarrow {a^2} = {\left( {a - 4} \right)^2} + {\left( {a - 2} \right)^2}\\ \Rightarrow {a^2} - 12a + 20 = 0\\ \Rightarrow \left[ \begin{array}{l}a = 10\\a = 2\end{array} \right. \end{array}\)

Với \(a = b = 2\) ta có phương trình đường tròn (C) là: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\)

Với \(a = b = 10\) ta có phương trình đường tròn (C) là: \({\left( {x - 10} \right)^2} + {\left( {y - 10} \right)^2} = 100\)

a) 

Gọi đường tròn cần tìm có dạng (C): \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\)

với tâm I(a;b) bán kính R

\(d\left(I,Ox\right)=\frac{\left|b\right|}{\sqrt{0^2+1^2}}=\left|b\right|\)

\(d\left(I,Oy\right)=\frac{\left|a\right|}{\sqrt{1^2}}=\left|a\right|\)

Do (C) tiếp xúc với Ox , Oy

\(\Rightarrow\left|a\right|=\left|b\right|=R\\ \Rightarrow a=\pm b\)

Lại có : (C) đi qua điểm có tọa độ (2;1) 

\(\Rightarrow\left(2-a\right)^2+\left(1-b\right)^2=b^2\left(vìb^2=R^2\right)\\ \Rightarrow a^2-4a+4+b^2-2b+1=b^2\\ \Leftrightarrow a^2-4a-2b+5=0\left(1\right)\)

TH1: a = b thay vào (1) ta được : 

\(\Rightarrow a^2-4a-2a+5=0\\ \Leftrightarrow a^2-6a+5=0\\ \Leftrightarrow a=1hoặca=5\)

với a =1 \(\Rightarrow\) b =1

\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=1\)

với \(a=5\Rightarrow b=5\\ \Rightarrow\left(C\right):\left(x-5\right)^2+\left(y-5\right)^2=25\)

TH2 : a = -b thay vào (1) ta được :

\(a^2-4a+2b+5=0\\ \Leftrightarrow a^2-2a+5=0\left(VôNgiệm\right)\)

Vậy có 2 đường tròn (C) cần tìm ở trên

b)

Gọi đường tròn cần tìm có dạng (C): \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) với tâm I (a;b), bán kính R

Do (C) đi qua 2 điểm (1;1) , (1;4) nên ta có :

\(\begin{cases}\left(1-a\right)^2+\left(1-b\right)^2=R^2\left(1\right)\\\left(1-a\right)^2+\left(4-b\right)^2=R^2\end{cases}\) 

\(\Rightarrow\left(1-b\right)^2=\left(4-b\right)^2\\ \Rightarrow b=\frac{5}{2}\)

Lại có : (C) tiếp xúc với Ox 

\(d\left(I,Ox\right)=\left|b\right|=R\\ \Rightarrow R=\frac{5}{2}\) 

Thay \(b=R=\frac{5}{2}\) vào (1)ta được :

\(\left(1-a\right)^2+\left(1-\frac{5}{2}\right)^2=\frac{25}{4}\\ \Leftrightarrow a^2-2a-3=0\\ \Leftrightarrow a=-1hoặca=3\)

với \(\begin{cases}a=-1\\b=R=\frac{5}{2}\end{cases}\) \(\Rightarrow\left(C\right):\left(x+1\right)^2+\left(y-\frac{5}{2}\right)^2=\frac{25}{4}\)

với \(\begin{cases}a=3\\b=R=\frac{5}{2}\end{cases}\) \(\Rightarrow\left(C\right):\left(x-3\right)^2+\left(y-\frac{5}{2}\right)^2=\frac{25}{4}\)

kksjknkjkjdcrf

 Gọi I(a,b) là tâm của đường tròn 
vì đường tròn tiếp xúc với 2 trục tọa độ nên tâm I nằm trên 1 trong các tia phân giác của các trục, nói cách khác là I cách đều hai trục tọa độ => |a| = |b| 
nhận xét: đường tròn tiếp xúc với 2 trục tọa độ nên cả hình tròn nằm trong 1 trong 4 góc của hệ trục, lại có A(2, -1) thuộc phần tư thứ IV => tâm I thuộc phần tư thứ IV => a > 0, b < 0 
như vậy tọa độ tâm là I(a, -a), bán kính R = a, với a > 0 

ptrình đường tròn: (x-a)² + (y+a)² = a² 
A(2, -1) thuộc đtròn <=> (2-a)² + (-1+a)² = a² <=> a² - 6a + 5 = 0 <=> a = 1 hoặc a = 5 

Vậy có 2 đường tròn thỏa yêu cầu là: (x-1)² + (y+1)² = 1 hoặc (x-5)² + (y-5)² = 25 

bn ơi , điểm có tọa độ là (2,1) mà bn , nhầm rùi kìa 

Bạn ơi,tại bạn này chép lời giải trên mạng nên chưa kịp sửa.