Xét ΔABC có BC^2=AB^2+AC^2

nen ΔABC vuông tại A

\(BD=\sqrt{2^2+9^2}=\sqrt{85}\left(cm\right)\)

a) Do 9²+12²=15² nên là tam giác vuông( định lý pytago)

b) Do B là trung điểm của đoạn AD nên AB và BD đối nhau. Suy ra AD vuông góc AC.

Lại thấy: B là trung điểm AD(gt) nên AD=2AB=18(cm)

Xét tan giác vuông ACD(cmt). Áp dụng định lí Pytago có:

AD²+AC²=DC²

<=>18²+15²=DC²

<=>324+225=DC²

<=>DC²=549(cm)

<=>DC=\(3\sqrt{61}\left(cm\right)\)

Vậy...

Bài 3. Cho tam giác
ABC
. Trên cạnh
AC
lấy điểm
N
sao cho

2
5
CN
AN
 . Trên cạnh BC lấy điểm
M
sao cho
BC xMC 

và MN // AB.

Tìm x.
A. 5 B. 2,5 C. 3,5 D. 1,4

a)Xét  \(\Delta ABC\) vuông tại A có :

    \(BC^2=AB^2+AC^2\) (định lý pytago)

    \(225=AB^2+144\)

\(\Rightarrow AB^2=225-144\)

     \(AB^2=81\)

     AB = 9cm

b)Xét \(\Delta ABD\) vuông tại A và \(\Delta EBD\) vuông tại E có :

   \(\widehat{ABD}=\widehat{EBD}\)

   BD chung

=>\(\Delta ABD\) =\(\Delta EBD\) (ch-gn)

=>\(\widehat{ADB}=\widehat{EDB}\)

=> DB là tia phân giác của \(\widehat{ADE}\)

c)M mình ko biết ở đâu nên mình ko làm nhé

Vì EF // BD nên \(\widehat{CFE}=\widehat{CDB}\)

Có : \(\widehat{CFE}+\widehat{EFD}=180^o\)

        \(\widehat{CDB}+\widehat{BDA}=180^o\)

mà \(\widehat{CFE}=\widehat{CDB}\)

=> \(\widehat{EFD}=\widehat{BDA}\)

mà \(\widehat{BDA}=\widehat{BDE}=\widehat{DEF}\)

=> \(\widehat{EFD}=\widehat{DEF}\) => \(\Delta DEF\) cân tại D

d) Có : \(AB=BE\) (\(\Delta ABD\) =\(\Delta EBD\))

=> \(\Delta ABE\) cân tại B

mà BD là đường phân giác của góc B 

=> BD là đường trung trực của AE

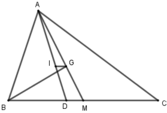
Do M là trung điểm BC nên MB = 1 2 BC = 1 2 .15 = 7,5 cm

Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm

Do IG // DM nên I G D M = A G A M = 2 3  => IG = 2 3 DM = 1 3 .1,5 = 1 cm

Đáp án: A

5:

1: BE//AC

AC vuông góc BD

=>BE vuông góc BD

=>ΔBED vuông tại B

2: 

DH=căn BD^2-BH^2=9cm

ΔBED vuông tại B có BH là đường cao

nên BD^2=DH*DE

=>DE=15^2/9=25cm

BE=căn 25^2-15^2=20(cm)

Xét tam giác ADB có góc ABD  = BAD = 60 độ => tam giác ABD đều => AB = BD = 7 cm

Tam giác ABD có AH nên trung tuyến nên đòng thời là đường cao

Áp dụng địa lý Pi - ta - go trong tam giác vuông ABH có AH = AB - BH = 7 - 3,5 = 36,75

HC = BC - BH = 15 - 3,5 = 11,5

Tam giác AHC có AC = AH + HC = 36,75 + 11 ,5 = 169

a: AB<AC<BC

=>góc C<góc B<góc A

b: Xét ΔABC vuông tại A và ΔADC vuông tại A có

AB=AD

AC chung

=>ΔABC=ΔADC

=>CB=CD
=>ΔCBD cân tại C