Cho tam giác ABC có O là điểm nằm trong góc ABC (và nằm ngoài tam giác ABC ) . Từ A' kẻ đường thẳng song song với AB tại B' . Từ B' kẻ đường thẳng song song với AB cắt OB tại B' . Chứng minh tam giác A'B'C' đồng dạng với tam giác ABC

Những câu hỏi liên quan
Cho tam giác ABC, phân giác AD, qua D kẻ đường thẳng song song với AB cắt AC tại E. Qua E kẻ đường thẳng song song với BC cắt AB tại Fa) Chứng minh AEBFb) Kẻ phân giác ngoài tại A của tam giác ABC cắt DE tại G. Chứng minh rằng E là trung điểm của DGc) Đường thẳng vuông góc với AD tại D cắt AB, AC lần lượt tại H, K. Chứng minh AH2FBd) Từ E kẻ đường thẳng song song với DK cắt AD tại I.Chứng minh H, I, G thẳng hàng
Đọc tiếp
Cho tam giác ABC, phân giác AD, qua D kẻ đường thẳng song song với AB cắt AC tại E. Qua E kẻ đường thẳng song song với BC cắt AB tại F
a) Chứng minh AE=BF
b) Kẻ phân giác ngoài tại A của tam giác ABC cắt DE tại G. Chứng minh rằng E là trung điểm của DG
c) Đường thẳng vuông góc với AD tại D cắt AB, AC lần lượt tại H, K. Chứng minh AH=2FB
d) Từ E kẻ đường thẳng song song với DK cắt AD tại I.Chứng minh H, I, G thẳng hàng
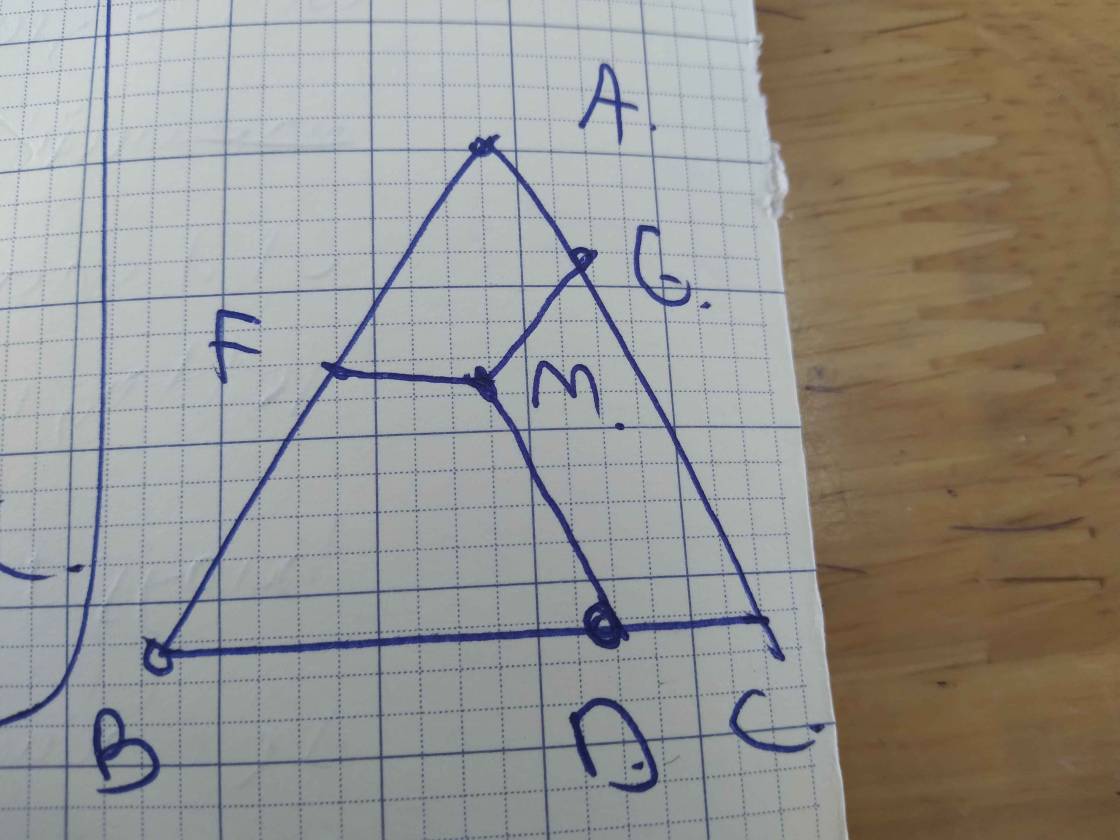
Cho tam giác ABC đều, M là điểm nằm trong tam giác đó. Qua M kẻ đường thẳng song song với AC và cắt BC ở D , kẻ đường thẳng song song với AB cắt AC tại E , kẻ đường thẳng song song với BC và cắt AB ở F . CM
A) Từ giác BFMD, CDME, AEMF là các hình thang cân .
B) tính số đo DME, EMF, DMF
Cho tam giác đều ABC và M nằm giữa B và C. Đường thẳng kẻ qua M và song song với AC cắt AB tại P, đường thẳng kẻ qua M và song song với AB cắt AC tại M. a, Chứng minh tam giác BPM và tam giác MCN là các tam giác cân. b, Gọi giao điểm của AM và PN là I . Gọi O là trọng tâm của tam giác ABC. Chứng minh tam giác OAN và tam giác OBP. c, Chứng minh OI là đường trung trực của NP.
Đọc tiếp
Cho tam giác đều ABC và M nằm giữa B và C. Đường thẳng kẻ qua M và song song với AC cắt AB tại P, đường thẳng kẻ qua M và song song với AB cắt AC tại M.
a, Chứng minh tam giác BPM và tam giác MCN là các tam giác cân.
b, Gọi giao điểm của AM và PN là I . Gọi O là trọng tâm của tam giác ABC. Chứng minh tam giác OAN và tam giác OBP.
c, Chứng minh OI là đường trung trực của NP.
Bài 7 : Cho tam giác ABC Qua A kẻ đường thẳng song song với BC ,qua C kẻ đường thẳng song song với AB hai đường thẳng này cắt nhau tại D a. Chứng minh tam giác ABC bằng tam giác ADC b. Chứng minh hai tam giác ADB &CBD bằng nhau c. Gọi O là giao điểm của AC&BD .Chứng minh hai tam giác ABO&COD bằng nhau
a: Xét ΔABC và ΔCDA có
\(\widehat{BAC}=\widehat{DCA}\)
AC chung
\(\widehat{ACB}=\widehat{CAD}\)
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC=ΔCDA
nên AB=CD và BC=DA
Xét ΔADB và ΔCBD có
AD=BC
AB=CD
DB chung
Do đó: ΔADB=ΔCBD
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC Qua A kẻ đường thẳng song song với BC ,qua C kẻ đường thẳng song song với AB hai đường thẳng này cắt nhau tại D a. Chứng minh tam giác ABC bằng tam giác ADC b. Chứng minh hai tam giác ADB &CBD bằng nhau c. Gọi O là giao điểm của AC&BD .Chứng minh hai tam giác ABO&COD bằng nhau
a: Xét ΔABC và ΔCDA có
\(\widehat{BAC}=\widehat{DCA}\)
AC chung
\(\widehat{ACB}=\widehat{CAD}\)
Do đó: ΔABC=ΔCDA
b: Xét ΔADB và ΔCBD có
BD chung
AD=CB
AB=CD
Do đó: ΔADB=ΔCBD
Đúng 1
Bình luận (0)
cho tam giác đều ABC ,M nằm trong tam giác đó.Qua M kẻ đường thẳng song song với AC và cắt BC tại D, kẻ đường thẳng song song với AB cắt AC tại E,kẻ đường thẳng song song vớiBC cắt AB ở F. gọi h là trung điểm của ef . cm:a) ae=mf b)3 điểm a;i;m thẳng hàng
Cho tam giác ABC . Gọi I là giao điểm của các đường phân giác trong của các góc của tam giác . từ I kẻ IM vuông góc AB , IN vuông góc với BC , IK vuông góc với AC . Qua A kẻ đường thẳng d1 song song MN , d1 cắt đường thẳng NK tại E . Qua a kẻ đường thẳng d2 cắt MN tại D . Đường thẳng ED cắt AC , AB lần lượt tại B và Q . CHỨNG MINH P, Q là đường trung bình của tam giác ABC
1 like
Cho tam giác ABC. Kẻ phân giác trong và phân giác ngoài của góc B cắt AC ở I và D. Từ I và D kẻ đường thẳng song song với BC cắt AB ở M và N. a) Tính AB và MN, biết MI = 12cm, BC = 20cm. b) Từ C kẻ đường thẳng song song với AB cắt BI tại E và cắt BD tại F. Chứng minh rằng: BI.IC = AI.IE và CE = CF.
Cho tam giác ABC vuông tại A có AB AC Gọi I là trung điểm của BC D là trung điểm của AC a chứng minh tam giác amb bằng tam giác ABC và AE vuông góc với BC b từ A kẻ đường thẳng vuông góc với BD cắt BC tại D trên tia đối của tia de lấy điểm F sao cho de AB Chứng minh rằng tam giác ADM bằng C D E Từ đó suy ra AE AB song song với CD e từ C kẻ đường thẳng vuông góc với AC cắt tại g Chứng minh tam giác ABD bằng tam giác ABC Chứng minh rằng AB ACG
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = AC Gọi I là trung điểm của BC D là trung điểm của AC a chứng minh tam giác amb bằng tam giác ABC và AE vuông góc với BC b từ A kẻ đường thẳng vuông góc với BD cắt BC tại D trên tia đối của tia de lấy điểm F sao cho de = AB Chứng minh rằng tam giác ADM bằng C D E Từ đó suy ra AE = AB song song với CD e từ C kẻ đường thẳng vuông góc với AC cắt tại g Chứng minh tam giác ABD bằng tam giác ABC Chứng minh rằng AB = ACG