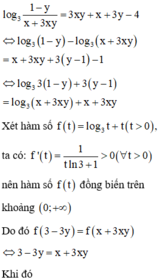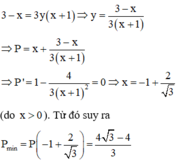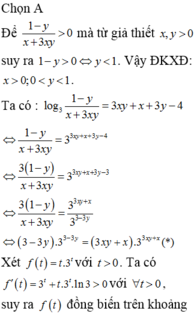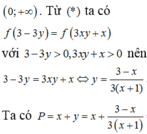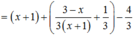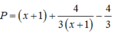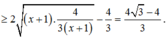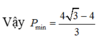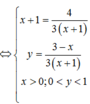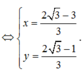Tìm các số nguyên x,y thoả mãn: 3xy+x-3y\(3xy+x-3y=5\)

Những câu hỏi liên quan
Xét các số thực dương x, y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P
m
i
n...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
A. P m i n = 4 3 + 4 3
B. P m i n = 4 3 - 4 3
C. P m i n = 4 3 - 4 9
D. P m i n = 4 3 + 4 9
Xét các số thực dương x, y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P
m
i
n...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
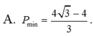
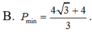
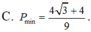
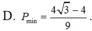
1, Tìm tất cả các số nguyên x, y thỏa mãn phương trình 2x ^ 2 + y ^ 2 + 3xy - 3x - 3y + 11 = 0
Ta có: \(2x^2+y^2+3xy-3x-3y+11=0\)
=>\(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
\(\Delta=\left(3y-3\right)^2-4\cdot2\cdot\left(y^2-3y+11\right)\)
\(=9y^2-18y+9-8y^2+24y-88=y^2+6y-79\)
\(=y^2+6y+9-88=\left(y+3\right)^2-88\)
Để phương trình có nghiệm nguyên thì Δ phải là số chính phương
=>\(\left(y+3\right)^2-88=k^2\left(k\in Z\right)\)
=>\(\left(y+3\right)^2-k^2=88\)
=>(y+3-k)(y+3+k)=88
=>(y+3-k;y+3+k)∈{(1;88);(88;1);(-1;-88);(-88;-1);(2;44);(44;2);(-2;-44);(-44;-2);(4;22);(-4;-22);(22;4);(-22;-4);(8;11);(-8;-11);(11;8);(-11;-8)}
TH1: y+3-k=1 và y+3+k=88
=>y+3-k+y+3+k=1+88
=>2y+6=89
=>2y=83
=>y=41,5(loại)
TH2: y+3-k=88 và y+3+k=1
=>y+3-k+y+3+k=1+88
=>2y+6=89
=>2y=83
=>y=41,5(loại)
TH3: y+3-k=-1 và y+3+k=-88
=>=>y+3-k+y+3+k=-1-88
=>2y+6=-89
=>2y=-95
=>y=-47,5(loại)
TH4: y+3-k=-88 và y+3+k=-1
=>=>y+3-k+y+3+k=-1-88
=>2y+6=-89
=>2y=-95
=>y=-47,5(loại)
TH5: y+3-k=2 và y+3+k=44
=>y+3-k+y+3+k=2+44
=>2y+6=46
=>2y=40
=>y=20(nhận)
\(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x^2+x\left(3\cdot20-3\right)+20^2-3\cdot20+11=0\)
=>\(2x^2+57x+351=0\)
=>\(\left(2x+39\right)\left(x+9\right)=0\)
=>\(\left[\begin{array}{l}2x+39=0\\ x+9=0\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=-39\\ x=-9\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-\frac{39}{2}\left(loại\right)\\ x=-9\left(nhận\right)\end{array}\right.\)
TH6: y+3-k=44 và y+3+k=2
=>y+3-k+y+3+k=2+44
=>2y+6=46
=>2y=40
=>y=20(nhận)
\(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x^2+x\left(3\cdot20-3\right)+20^2-3\cdot20+11=0\)
=>\(2x^2+57x+351=0\)
=>\(\left(2x+39\right)\left(x+9\right)=0\)
=>\(\left[\begin{array}{l}2x+39=0\\ x+9=0\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=-39\\ x=-9\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-\frac{39}{2}\left(loại\right)\\ x=-9\left(nhận\right)\end{array}\right.\)
TH7: y+3-k=-2 và y+3+k=-44
=>y+3-k+y+3+k=-2-44
=>2y+6=-46
=>2y=-52
=>y=-26
Ta có: \(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x^2+x\cdot\left\lbrack3\cdot\left(-26\right)-3\right\rbrack+\left(-26\right)^2-3\cdot\left(-26\right)+11=0\)
=>\(2x^2-81x+765=0\)
=>(x-15)(2x-51)=0
=>\(\left[\begin{array}{l}x-15=0\\ 2x-51=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=15\left(nhận\right)\\ x=\frac{51}{2}\left(loại\right)\end{array}\right.\)
TH8: y+3-k=-44 và y+3+k=-2
=>y+3-k+y+3+k=-2-44
=>2y+6=-46
=>2y=-52
=>y=-26
Ta có: \(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x^2+x\cdot\left\lbrack3\cdot\left(-26\right)-3\right\rbrack+\left(-26\right)^2-3\cdot\left(-26\right)+11=0\)
=>\(2x^2-81x+765=0\)
=>(x-15)(2x-51)=0
=>\(\left[\begin{array}{l}x-15=0\\ 2x-51=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=15\left(nhận\right)\\ x=\frac{51}{2}\left(loại\right)\end{array}\right.\)
TH9: y+3-k=4 và y+3+k=22
=>y+3-k+y+3+k=4+22
=>2y+6=26
=>2y=20
=>y=10
Ta có: \(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x_{}^2+x\left(3\cdot10-3\right)+10^2-3\cdot10+11=0\)
=>\(2x^2+27x+81=0\)
=>\(2x^2+18x+9x+81=0\)
=>(x+9)(2x+9)=0
=>\(\left[\begin{array}{l}x+9=0\\ 2x+9=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-9\left(nhận\right)\\ x=-\frac92\left(loại\right)\end{array}\right.\)
TH10: y+3-k=22 và y+3+k=4
=>y+3-k+y+3+k=4+22
=>2y+6=26
=>2y=20
=>y=10
Ta có: \(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x_{}^2+x\left(3\cdot10-3\right)+10^2-3\cdot10+11=0\)
=>\(2x^2+27x+81=0\)
=>\(2x^2+18x+9x+81=0\)
=>(x+9)(2x+9)=0
=>\(\left[\begin{array}{l}x+9=0\\ 2x+9=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-9\left(nhận\right)\\ x=-\frac92\left(loại\right)\end{array}\right.\)
TH11: y+3-k=-4 và y+3+k=-22
=>y+3-k+y+3+k=-4-22
=>2y+6=-26
=>2y=-32
=>y=-16
Ta có: \(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x_{}^2+x\cdot\left\lbrack3\cdot\left(-16\right)-3\right\rbrack+\left(-16\right)^2-3\cdot\left(-16\right)+11=0\)
=>\(2x^2-51x+315=0\)
=>\(2x^2-30x-21x+315=0\)
=>(x-15)(2x-21)=0
=>\(\left[\begin{array}{l}x-15=0\\ 2x-21=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=15\left(nhận\right)\\ x=\frac{21}{2}\left(loại\right)\end{array}\right.\)
TH12: y+3-k=-22 và y+3+k=-4
=>y+3-k+y+3+k=-4-22
=>2y+6=-26
=>2y=-32
=>y=-16
Ta có: \(2x^2+x\left(3y-3\right)+y^2-3y+11=0\)
=>\(2x_{}^2+x\cdot\left\lbrack3\cdot\left(-16\right)-3\right\rbrack+\left(-16\right)^2-3\cdot\left(-16\right)+11=0\)
=>\(2x^2-51x+315=0\)
=>\(2x^2-30x-21x+315=0\)
=>(x-15)(2x-21)=0
=>\(\left[\begin{array}{l}x-15=0\\ 2x-21=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=15\left(nhận\right)\\ x=\frac{21}{2}\left(loại\right)\end{array}\right.\)
TH13: y+3-k=8 và y+3+k=11
=>y+3-k+y+3+k=8+11
=>2y+6=19
=>2y=13
=>y=6,5(loại)
TH14: y+3-k=11 và y+3+k=8
=>y+3-k+y+3+k=8+11
=>2y+6=19
=>2y=13
=>y=6,5(loại)
TH15: y+3-k=-8 và y+3+k=-11
=>y+3-k+y+3+k=-8-11
=>2y+6=-19
=>2y=-25
=>y=-12,5(loại)
TH16: y+3-k=-11 và y+3+k=-8
=>y+3-k+y+3+k=-8-11
=>2y+6=-19
=>2y=-25
=>y=-12,5(loại)
Đúng 0
Bình luận (0)
Tìm các cặp số nguyên x, y thoả mãn : X^3 + 3XY + 2Y - 5 = 0
tìm số nguyên x, y thỏa mãn: a, 3x[y+1]+y+1=7 b, xy-x+3y-3=5 c,2xy+x+y=7 d,3xy-2x+5y=29
a, 3x ( y+1) + y + 1 = 7
(y+1)(3x +1) =7
th1 : \(\left\{{}\begin{matrix}y+1=1\\3x+1=7\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=0\\x=2\end{matrix}\right.\)
th2: \(\left\{{}\begin{matrix}y+1=-1\\3x+1=-7\end{matrix}\right.\)=> x = -8/3 (loại)
th3: \(\left\{{}\begin{matrix}y+1=7\\3x+1=1\end{matrix}\right.\)=> \(\left\{{}\begin{matrix}y=6\\x=0\end{matrix}\right.\)
th 4 : \(\left\{{}\begin{matrix}y+1=-7\\3x+1=-1\end{matrix}\right.\)=> x=-2/3 (loại)
Vậy (x,y)= (2 ;0); (0; 6)
b, xy - x + 3y - 3 = 5
(x( y-1) + 3( y-1) = 5
(y-1)(x+3) = 5
th1: \(\left\{{}\begin{matrix}y-1=1\\x+3=5\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=2\\x=8\end{matrix}\right.\)
th2: \(\left\{{}\begin{matrix}y-1=-1\\x+3=-5\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=0\\x=-8\end{matrix}\right.\)
th3: \(\left\{{}\begin{matrix}y-1=5\\x+3=1\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=6\\x=-2\end{matrix}\right.\)
th4: \(\left\{{}\begin{matrix}y-1=-5\\x+3=-1\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=-4\\x=-4\end{matrix}\right.\)
vậy (x, y) = ( 8; 2); ( -8; 0); (-2; 6); (-4; -4)
c, 2xy + x + y = 7 => y = \(\dfrac{7-x}{2x+1}\) ; y ϵ Z ⇔ 7-x ⋮ 2x+1
⇔ 14 - 2x ⋮ 2x + 1 ⇔ 15 - 2x - 1 ⋮ 2x + 1
th1 : 2x + 1 = -1=> x = -1; y = \(\dfrac{7-(-1)}{-1.2+1}\) = -8
th2: 2x+ 1 = 1=> x =0; y = 7
th3: 2x+1 = -3 => x = x=-2 => y = \(\dfrac{7-(-2)}{-2.2+1}\) = -3
th4: 2x+ 1 = 3 => x = 1 => y = \(\dfrac{7+1}{2.1+1}\) = 2
th5: 2x + 1 = -5 => x = -3=> y = \(\dfrac{7-(-3)}{-3.2+1}\) = -2
th6: 2x + 1 = 5 => x = 2; ; y = \(\dfrac{7-2}{2.2+1}\) =1
th7 : 2x + 1 = -15 => x = -8; y = \(\dfrac{7-(-8)}{-8.2+1}\) = -1
th8 : 2x+1 = 15 => x = 7; y = \(\dfrac{7-7}{2.7+1}\) = 0
kết luận
(x,y) = (-1; -8); (0 ;7); ( -2; -3) ; ( 1; 2); ( -3; -2); (2;1); (-8;-1);(7;0)
Đúng 3
Bình luận (0)
3xy−2x+5y=293xy−2x+5y=29
9xy−6x+15y=879xy−6x+15y=87
(9xy−6x)+(15y−10)=77(9xy−6x)+(15y−10)=77
3x(3y−2)+5(3y−2)=773x(3y−2)+5(3y−2)=77
(3y−2)(3x+5)=77(3y−2)(3x+5)=77
⇒(3y−2)⇒(3y−2) và (3x+5)(3x+5) là Ư(77)=±1,±7,±11,±77Ư(77)=±1,±7,±11,±77
Ta có bảng giá trị sau:
Do x,y∈Zx,y∈Z nên (x,y)∈{(−4;−3),(−2;−25),(2;3),(24;1)}
Đúng 0
Bình luận (0)
Xét các số thực dương x;y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P...
Đọc tiếp
Xét các số thực dương x;y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của biểu thức P=x+y..
A. P m i n = 4 3 - 4 3
B. P m i n = 4 3 + 4 3
C. P m i n = 4 3 + 4 9
D. P m i n = 4 3 - 4 9
ĐK:
![]()
Ta có
log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4
![]()
![]()
![]()

Xét hàm số f ( x ) = log 3 t + 3 t t > 0
có f ' ( t ) = 1 t ln 3 + 3 > 0 ; ∀ t > 0 nên hàm số đồng biến trên 0 ; + ∞
Kết hợp (*) suy ra
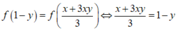
![]()
Xét P = x + y ⇒ x = P - y thay vào (**) ta được
![]()
![]()
Ta tìm giá trị nhỏ nhất của g ( y ) = 3 y 2 - 2 y + 3 3 y + 1 trên (0;1)
Ta có
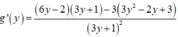
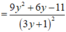
Giải phương trình
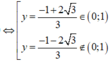
Lại có g ' ( y ) < 0 ∀ y ∈ 0 ; - 1 + 2 3 3
và g ' ( y ) > 0 ∀ y ∈ - 1 + 2 3 3 ; 1
Hay g'(y) đổi dấu từ âm sang dương tại y = - 1 + 2 3 3 nên
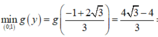
⇒ P m i n = 4 3 - 4 3
Chọn đáp án A.
Đúng 0
Bình luận (0)
Xét các số thực dương x;y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P...
Đọc tiếp
Xét các số thực dương x;y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của biểu thức P = x + y.
A. P m i n = 4 3 - 4 3
B. P m i n = 4 3 + 4 3
C. P m i n = 4 3 + 4 9
D. P m i n = 4 3 - 4 9
Tìm các số nguyên x,y thoả mãn: 3xy+2x-5y=6
Lời giải:
$3xy+2x-5y=6$
$x(3y+2)-5y=6$
$3x(3y+2)-15y=18$
$3x(3y+2)-5(3y+2)=8$
$(3y+2)(3x-5)=8$
Đến đây lập bảng xét giá trị thôi bạn.

Đúng 10
Bình luận (0)
3xy+2x−5y=6
𝑥
(
3
𝑦
+
2
)
−
5
𝑦
=
6
x(3y+2)−5y=6
3
𝑥
(
3
𝑦
+
2
)
−
15
𝑦
=
18
3x(3y+2)−15y=18
3
𝑥
(
3
𝑦
+
2
)
−
5
(
3
𝑦
+
2
)
=
8
3x(3y+2)−5(3y+2)=8
(
3
𝑦
+
2
)
(
3
𝑥
−
5
)
=
8
(3y+2)(3x−5)=8
Đến đây lập bảng xét giá trị thôi bạn.
Đúng 1
Bình luận (0)
Tìm các số nguyên x,y thoả mãn :
a,\(5.\left(x+y\right)+2=3xy\)
b,\(2\left(x+y\right)+16=3xy\)
b. Câu hỏi của Tiểu thư họ Vũ - Toán lớp 9 - Học toán với OnlineMath